26. (12 分)阅读材料 1:
对于两个正实数 $ a $,$ b $,由于 $ ( \sqrt { a } - \sqrt { b } ) ^ { 2 } \geqslant 0 $,所以 $ ( \sqrt { a } ) ^ { 2 } - 2 \sqrt { a } \cdot \sqrt { b } + ( \sqrt { b } ) ^ { 2 } \geqslant 0 $,即 $ a - 2 \sqrt { a b } + b \geqslant 0 $,所以得到 $ a + b \geqslant 2 \sqrt { a b } $,并且当 $ a = b $ 时,$ a + b = 2 \sqrt { a b } $.
阅读材料 2:
若 $ x > 0 $,则 $ \frac { x ^ { 2 } + 1 } { x } = \frac { x ^ { 2 } } { x } + \frac { 1 } { x } = x + \frac { 1 } { x } $,因为 $ x > 0 $,$ \frac { 1 } { x } > 0 $,所以由阅读材料 1 可得,$ x + \frac { 1 } { x } \geqslant 2 \sqrt { x \cdot \frac { 1 } { x } } = 2 $,即 $ \frac { x ^ { 2 } + 1 } { x } $ 的最小值是 2,只有当 $ x = \frac { 1 } { x } $ 时,即 $ x = 1 $ 时取得最小值.
根据以上阅读材料,请回答以下问题:
(1)比较大小:
$ x ^ { 2 } + 1 $______$ 2 x $(其中 $ x \geqslant 1 $);
$ x + \frac { 1 } { x } $______$ - 2 $(其中 $ x < - 1 $).
(2)已知代数式 $ \frac { x ^ { 2 } + 3 x + 3 } { x + 1 } $ 变形为 $ x + n + \frac { 1 } { x + 1 } $,求常数 $ n $ 的值;
(3)当 $ x = $______时,$ \frac { x + 3 + 3 \sqrt { x } } { \sqrt { x } + 1 } $ 有最小值,最小值为______(直接写出答案).
(1)
(2) n=
(3)当 $ x = $
对于两个正实数 $ a $,$ b $,由于 $ ( \sqrt { a } - \sqrt { b } ) ^ { 2 } \geqslant 0 $,所以 $ ( \sqrt { a } ) ^ { 2 } - 2 \sqrt { a } \cdot \sqrt { b } + ( \sqrt { b } ) ^ { 2 } \geqslant 0 $,即 $ a - 2 \sqrt { a b } + b \geqslant 0 $,所以得到 $ a + b \geqslant 2 \sqrt { a b } $,并且当 $ a = b $ 时,$ a + b = 2 \sqrt { a b } $.
阅读材料 2:
若 $ x > 0 $,则 $ \frac { x ^ { 2 } + 1 } { x } = \frac { x ^ { 2 } } { x } + \frac { 1 } { x } = x + \frac { 1 } { x } $,因为 $ x > 0 $,$ \frac { 1 } { x } > 0 $,所以由阅读材料 1 可得,$ x + \frac { 1 } { x } \geqslant 2 \sqrt { x \cdot \frac { 1 } { x } } = 2 $,即 $ \frac { x ^ { 2 } + 1 } { x } $ 的最小值是 2,只有当 $ x = \frac { 1 } { x } $ 时,即 $ x = 1 $ 时取得最小值.
根据以上阅读材料,请回答以下问题:
(1)比较大小:
$ x ^ { 2 } + 1 $______$ 2 x $(其中 $ x \geqslant 1 $);
$ x + \frac { 1 } { x } $______$ - 2 $(其中 $ x < - 1 $).
(2)已知代数式 $ \frac { x ^ { 2 } + 3 x + 3 } { x + 1 } $ 变形为 $ x + n + \frac { 1 } { x + 1 } $,求常数 $ n $ 的值;
(3)当 $ x = $______时,$ \frac { x + 3 + 3 \sqrt { x } } { \sqrt { x } + 1 } $ 有最小值,最小值为______(直接写出答案).
(1)
≥
;<
;(2) n=
2
;(3)当 $ x = $
0
时,$ \frac { x + 3 + 3 \sqrt { x } } { \sqrt { x } + 1 } $ 有最小值,最小值为3
(直接写出答案).答案:
(1) ≥; <;
(2) n=2;
(3) 0; 3
(1) ≥; <;
(2) n=2;
(3) 0; 3
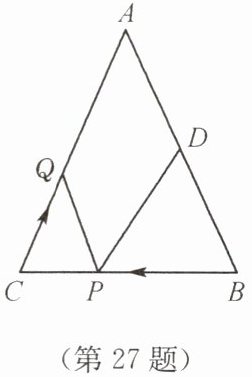
27. (16 分)如图,已知 $ \triangle A B C $ 中,$ \angle B = \angle C $,$ A B = 8 \mathrm { cm } $,$ B C = 6 \mathrm { cm } $,点 $ D $ 为 $ A B $ 的中点. 如果点 $ P $ 在线段 $ B C $ 上以每秒 $ 2 \mathrm { cm } $ 的速度由点 $ B $ 向点 $ C $ 运动,同时,点 $ Q $ 在线段 $ C A $ 上以每秒 $ a \mathrm { cm } $ 的速度由点 $ C $ 向点 $ A $ 运动,设运动时间为 $ t ( \mathrm { s } ) $($ 0 \leqslant t \leqslant 3 $).
(1)用含 $ t $ 的代数式表示 $ P C $ 的长度;
(2)若点 $ P $,$ Q $ 的运动速度相等,经过 $ 1 \mathrm { s } $ 后,$ \triangle B P D $ 与 $ \triangle C Q P $ 是否全等?请说明理由.
(3)若点 $ P $,$ Q $ 的运动速度不相等,当点 $ Q $ 的运动速度 $ a $ 为多少时,能够使 $ \triangle B P D $ 与 $ \triangle C Q P $ 全等?
(1)用含 $ t $ 的代数式表示 $ P C $ 的长度;
(2)若点 $ P $,$ Q $ 的运动速度相等,经过 $ 1 \mathrm { s } $ 后,$ \triangle B P D $ 与 $ \triangle C Q P $ 是否全等?请说明理由.
(3)若点 $ P $,$ Q $ 的运动速度不相等,当点 $ Q $ 的运动速度 $ a $ 为多少时,能够使 $ \triangle B P D $ 与 $ \triangle C Q P $ 全等?

答案:提示:
(1) BP=2t, 则PC=BC-BP=6-2t;
(2) △BPD和△CQP全等, 由SAS可证得;
(3)
∵点P, Q的运动速度不相等,
∴BP≠CQ. 又
∵∠B=∠C,
∴BP=PC=3 cm, CQ=BD=4 cm,
∴点P, Q运动的时间$t=\frac{BP}{2}=\frac{3}{2} s, $
∴$v_Q=\frac{CQ}{t}=4÷\frac{3}{2}=\frac{8}{3} cm/s$
(1) BP=2t, 则PC=BC-BP=6-2t;
(2) △BPD和△CQP全等, 由SAS可证得;
(3)
∵点P, Q的运动速度不相等,
∴BP≠CQ. 又
∵∠B=∠C,
∴BP=PC=3 cm, CQ=BD=4 cm,
∴点P, Q运动的时间$t=\frac{BP}{2}=\frac{3}{2} s, $
∴$v_Q=\frac{CQ}{t}=4÷\frac{3}{2}=\frac{8}{3} cm/s$