21. (12 分)解方程:
(1)$ \frac { 1 - x } { x - 2 } = \frac { 1 } { 2 - x } - 2 $;
(2)$ \frac { 2 x } { 2 x - 1 } + \frac { x } { x - 2 } = 2 $.
(1)$ \frac { 1 - x } { x - 2 } = \frac { 1 } { 2 - x } - 2 $;
(2)$ \frac { 2 x } { 2 x - 1 } + \frac { x } { x - 2 } = 2 $.
答案:
(1) 无解$; (2) x=\frac{4}{5}$
(1) 无解$; (2) x=\frac{4}{5}$
解析:
(1)方程两边同乘$(x-2)$,得$1-x=-1-2(x-2)$
去括号,得$1-x=-1-2x+4$
移项、合并同类项,得$x=2$
检验:当$x=2$时,$x-2=0$,所以$x=2$是原分式方程的增根,原分式方程无解
(2)方程两边同乘$(2x-1)(x-2)$,得$2x(x-2)+x(2x-1)=2(2x-1)(x-2)$
去括号,得$2x^{2}-4x+2x^{2}-x=4x^{2}-10x+4$
移项、合并同类项,得$5x=4$
解得$x=\frac{4}{5}$
检验:当$x=\frac{4}{5}$时,$(2x-1)(x-2)\neq0$,所以$x=\frac{4}{5}$是原分式方程的解
22. (10 分)若方程 $ \frac { 3 } { x + 3 } = \frac { 2 } { x + k } $ 有负数根,求 $ k $ 的取值范围.
答案:k>2且k≠3
解析:
方程两边同乘$(x+3)(x+k)$,得$3(x+k)=2(x+3)$,
去括号,得$3x+3k=2x+6$,
移项、合并同类项,得$x=6-3k$,
因为方程有负数根,所以$x=6-3k<0$,解得$k>2$,
又因为分母不能为零,所以$x+3\neq0$且$x+k\neq0$,
即$6-3k+3\neq0$且$6-3k+k\neq0$,
$9-3k\neq0$解得$k\neq3$,
$6-2k\neq0$解得$k\neq3$,
综上,$k$的取值范围是$k>2$且$k\neq3$。
去括号,得$3x+3k=2x+6$,
移项、合并同类项,得$x=6-3k$,
因为方程有负数根,所以$x=6-3k<0$,解得$k>2$,
又因为分母不能为零,所以$x+3\neq0$且$x+k\neq0$,
即$6-3k+3\neq0$且$6-3k+k\neq0$,
$9-3k\neq0$解得$k\neq3$,
$6-2k\neq0$解得$k\neq3$,
综上,$k$的取值范围是$k>2$且$k\neq3$。
23. (8 分)(1)填空:$ ( a - b ) ( a + b ) = $
$ ( a - b ) ( a ^ { 2 } + a b + b ^ { 2 } ) = $
$ ( a - b ) ( a ^ { 3 } + a ^ { 2 } b + a b ^ { 2 } + b ^ { 3 } ) = $
(2)猜想:$ ( a - b ) ( a ^ { n - 1 } + a ^ { n - 2 } b + … + a b ^ { n - 2 } + b ^ { n - 1 } ) = $
(3)利用(2)猜想的结论计算:$ 2 ^ { 9 } - 2 ^ { 8 } + 2 ^ { 7 } - … + 2 ^ { 3 } - 2 ^ { 2 } + 2 $.
$a^2 - b^2$
;$ ( a - b ) ( a ^ { 2 } + a b + b ^ { 2 } ) = $
$a^3 - b^3$
;$ ( a - b ) ( a ^ { 3 } + a ^ { 2 } b + a b ^ { 2 } + b ^ { 3 } ) = $
$a^4 - b^4$
.(2)猜想:$ ( a - b ) ( a ^ { n - 1 } + a ^ { n - 2 } b + … + a b ^ { n - 2 } + b ^ { n - 1 } ) = $
$a^n - b^n$
(其中 $ n $ 为正整数,且 $ n \geqslant 2 $).(3)利用(2)猜想的结论计算:$ 2 ^ { 9 } - 2 ^ { 8 } + 2 ^ { 7 } - … + 2 ^ { 3 } - 2 ^ { 2 } + 2 $.
342
答案:$(1) a^2-b^2, a^3-b^3, a^4-b^4; (2) a^n-b^n; (3) 342. $提示: 令$S=2^9-2^8+2^7-…+2^3-2^2+2, $
∴$S-1=2^9-2^8+2^7-…+2^3-2^2+2-1=[2-(-1)](2^9-2^8+2^7-…+2^3-2^2+2-1)÷3=(2^{10}-1)÷3=(1024-1)÷3=341, $
∴S=342
∴$S-1=2^9-2^8+2^7-…+2^3-2^2+2-1=[2-(-1)](2^9-2^8+2^7-…+2^3-2^2+2-1)÷3=(2^{10}-1)÷3=(1024-1)÷3=341, $
∴S=342
24. (8 分)已知:如图,$ O $ 为 $ \triangle A B C $ 的 $ \angle B A C $ 的角平分线上一点,$ \angle 1 = \angle 2 $,求证:$ \triangle A B C $ 是等腰三角形.
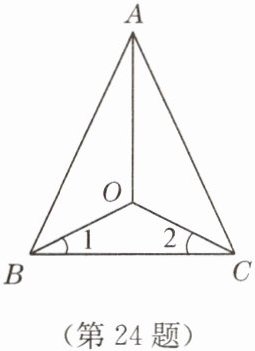

答案:解:过点$O$作$OD⊥ AB$于点$D$,$OE⊥ AC$于点$E$。
因为$AO$平分$\angle BAC$,根据角平分线的性质可知$OD = OE$(角平分线上的点到角两边的距离相等)。
在$\triangle OBD$和$\triangle OCE$中,$\{\begin{array}{l}\angle ODB=\angle OEC = 90^{\circ}\\\angle 1=\angle 2\\OD = OE\end{array} $,
所以$\triangle OBD\cong\triangle OCE(AAS)$,则$OB = OC$。
在$\triangle ABO$和$\triangle ACO$中,$\{\begin{array}{l}AO = AO\\\angle BAO=\angle CAO\\OB = OC\end{array} $,
所以$\triangle ABO\cong\triangle ACO(SAS)$,则$\angle ABC=\angle ACB$。
因为$\angle ABC=\angle ACB$,所以$AB = AC$(等角对等边),即$\triangle ABC$是等腰三角形。
因为$AO$平分$\angle BAC$,根据角平分线的性质可知$OD = OE$(角平分线上的点到角两边的距离相等)。
在$\triangle OBD$和$\triangle OCE$中,$\{\begin{array}{l}\angle ODB=\angle OEC = 90^{\circ}\\\angle 1=\angle 2\\OD = OE\end{array} $,
所以$\triangle OBD\cong\triangle OCE(AAS)$,则$OB = OC$。
在$\triangle ABO$和$\triangle ACO$中,$\{\begin{array}{l}AO = AO\\\angle BAO=\angle CAO\\OB = OC\end{array} $,
所以$\triangle ABO\cong\triangle ACO(SAS)$,则$\angle ABC=\angle ACB$。
因为$\angle ABC=\angle ACB$,所以$AB = AC$(等角对等边),即$\triangle ABC$是等腰三角形。
25. (10 分)甲、乙两商场自行定价销售某一商品.
(1)甲商场将该商品提价 $ 15 \% $ 后的售价为 1.15 元,则该商品在甲商场的原价为
(2)乙商场将该商品提价 $ 20 \% $ 后,用 6 元钱购买该商品的件数比提价前少买 1 件,求该商品在乙商场的原价是多少.
(3)甲、乙两商场把该商品均按原价进行了两次价格调整.
甲商场:第一次提价的百分率是 $ a $,第二次提价的百分率是 $ b $;
乙商场:两次提价的百分率都是 $ \frac { a + b } { 2 } $($ a > 0 $,$ b > 0 $,$ a \neq b $).
请问甲、乙两商场,哪个商场的提价较多?请说明理由.
由于原价均为1元, 则甲商场两次提价后的价格为(1+a)(1+b)=1+a+b+ab. 乙商场两次提价后的价格为$(1+\frac{a+b}{2})^2=1+a+b+(\frac{a+b}{2})^2.$
∵$(\frac{a+b}{2})^2-ab=(\frac{a-b}{2})^2>0,$
∴乙商场的提价较多
(1)甲商场将该商品提价 $ 15 \% $ 后的售价为 1.15 元,则该商品在甲商场的原价为
1
元;(2)乙商场将该商品提价 $ 20 \% $ 后,用 6 元钱购买该商品的件数比提价前少买 1 件,求该商品在乙商场的原价是多少.
设该商品在乙商场的原价为x元, 则$\frac{6}{x}-\frac{6}{1.2x}=1, $解得x=1. 经检验: x=1满足方程, 符合实际. 答: 该商品在乙商场的原价为1元.
(3)甲、乙两商场把该商品均按原价进行了两次价格调整.
甲商场:第一次提价的百分率是 $ a $,第二次提价的百分率是 $ b $;
乙商场:两次提价的百分率都是 $ \frac { a + b } { 2 } $($ a > 0 $,$ b > 0 $,$ a \neq b $).
请问甲、乙两商场,哪个商场的提价较多?请说明理由.
由于原价均为1元, 则甲商场两次提价后的价格为(1+a)(1+b)=1+a+b+ab. 乙商场两次提价后的价格为$(1+\frac{a+b}{2})^2=1+a+b+(\frac{a+b}{2})^2.$
∵$(\frac{a+b}{2})^2-ab=(\frac{a-b}{2})^2>0,$
∴乙商场的提价较多
答案:
(1) 1.15÷(1+15%)=1(元);
(2) 设该商品在乙商场的原价为x元, 则$\frac{6}{x}-\frac{6}{1.2x}=1, $解得x=1. 经检验: x=1满足方程, 符合实际. 答: 该商品在乙商场的原价为1元.
(3) 由于原价均为1元, 则甲商场两次提价后的价格为(1+a)(1+b)=1+a+b+ab. 乙商场两次提价后的价格为$(1+\frac{a+b}{2})^2=1+a+b+(\frac{a+b}{2})^2. $
∵$(\frac{a+b}{2})^2-ab=(\frac{a-b}{2})^2>0, $
∴乙商场的提价较多
(1) 1.15÷(1+15%)=1(元);
(2) 设该商品在乙商场的原价为x元, 则$\frac{6}{x}-\frac{6}{1.2x}=1, $解得x=1. 经检验: x=1满足方程, 符合实际. 答: 该商品在乙商场的原价为1元.
(3) 由于原价均为1元, 则甲商场两次提价后的价格为(1+a)(1+b)=1+a+b+ab. 乙商场两次提价后的价格为$(1+\frac{a+b}{2})^2=1+a+b+(\frac{a+b}{2})^2. $
∵$(\frac{a+b}{2})^2-ab=(\frac{a-b}{2})^2>0, $
∴乙商场的提价较多