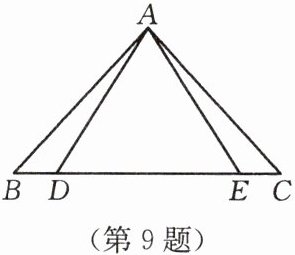
9. 如图,$ A B = A C $,$ A D = A E $,$ \angle B = 50 ^ { \circ } $,$ \angle A E C = 120 ^ { \circ } $,则 $ \angle D A C $ 的度数等于(
A.$ 120 ^ { \circ } $
B.$ 70 ^ { \circ } $
C.$ 60 ^ { \circ } $
D.$ 50 ^ { \circ } $
B
)
A.$ 120 ^ { \circ } $
B.$ 70 ^ { \circ } $
C.$ 60 ^ { \circ } $
D.$ 50 ^ { \circ } $
答案:B
解析:
解:
∵ $AB = AC$,
∴ $\angle B = \angle C = 50°$。
∵ $\angle AEC = 120°$,
∴ $\angle EAC = 180° - \angle AEC - \angle C = 180° - 120° - 50° = 10°$。
∵ $AD = AE$,
∴ $\angle ADE = \angle AED$。
∵ $\angle AED = 180° - \angle AEC = 180° - 120° = 60°$,
∴ $\angle DAE = 180° - 2\angle AED = 180° - 2 × 60° = 60°$。
∵ $\angle BAC = 180° - 2\angle B = 180° - 2 × 50° = 80°$,
∴ $\angle BAD = \angle BAC - \angle DAE - \angle EAC = 80° - 60° - 10° = 10°$。
∴ $\angle DAC = \angle DAE + \angle EAC = 60° + 10° = 70°$。
答案:B
∵ $AB = AC$,
∴ $\angle B = \angle C = 50°$。
∵ $\angle AEC = 120°$,
∴ $\angle EAC = 180° - \angle AEC - \angle C = 180° - 120° - 50° = 10°$。
∵ $AD = AE$,
∴ $\angle ADE = \angle AED$。
∵ $\angle AED = 180° - \angle AEC = 180° - 120° = 60°$,
∴ $\angle DAE = 180° - 2\angle AED = 180° - 2 × 60° = 60°$。
∵ $\angle BAC = 180° - 2\angle B = 180° - 2 × 50° = 80°$,
∴ $\angle BAD = \angle BAC - \angle DAE - \angle EAC = 80° - 60° - 10° = 10°$。
∴ $\angle DAC = \angle DAE + \angle EAC = 60° + 10° = 70°$。
答案:B
10. 观察下列各式及其展开式:
$ ( a + b ) ^ { 2 } = a ^ { 2 } + 2 a b + b ^ { 2 } $;
$ ( a + b ) ^ { 3 } = a ^ { 3 } + 3 a ^ { 2 } b + 3 a b ^ { 2 } + b ^ { 3 } $;
$ ( a + b ) ^ { 4 } = a ^ { 4 } + 4 a ^ { 3 } b + 6 a ^ { 2 } b ^ { 2 } + 4 a b ^ { 3 } + b ^ { 4 } $;
$ ( a + b ) ^ { 5 } = a ^ { 5 } + 5 a ^ { 4 } b + 10 a ^ { 3 } b ^ { 2 } + 10 a ^ { 2 } b ^ { 3 } + 5 a b ^ { 4 } + b ^ { 5 } $;
……
请你猜想 $ ( a + b ) ^ { 12 } $ 的展开式中第三项的系数是(
A.36
B.45
C.55
D.66
$ ( a + b ) ^ { 2 } = a ^ { 2 } + 2 a b + b ^ { 2 } $;
$ ( a + b ) ^ { 3 } = a ^ { 3 } + 3 a ^ { 2 } b + 3 a b ^ { 2 } + b ^ { 3 } $;
$ ( a + b ) ^ { 4 } = a ^ { 4 } + 4 a ^ { 3 } b + 6 a ^ { 2 } b ^ { 2 } + 4 a b ^ { 3 } + b ^ { 4 } $;
$ ( a + b ) ^ { 5 } = a ^ { 5 } + 5 a ^ { 4 } b + 10 a ^ { 3 } b ^ { 2 } + 10 a ^ { 2 } b ^ { 3 } + 5 a b ^ { 4 } + b ^ { 5 } $;
……
请你猜想 $ ( a + b ) ^ { 12 } $ 的展开式中第三项的系数是(
D
)A.36
B.45
C.55
D.66
答案:D
解析:
观察各式展开式系数规律:
$(a+b)^2$系数:1,2,1
$(a+b)^3$系数:1,3,3,1
$(a+b)^4$系数:1,4,6,4,1
$(a+b)^5$系数:1,5,10,10,5,1
系数呈现杨辉三角特征,第$n$行($n\geq2$)第3项系数为$\frac{(n-1)(n-2)}{2}$。
对于$(a+b)^{12}$,$n=12$,第三项系数为$\frac{(12-1)(12-2)}{2}=\frac{11×10}{2}=55$。
C
$(a+b)^2$系数:1,2,1
$(a+b)^3$系数:1,3,3,1
$(a+b)^4$系数:1,4,6,4,1
$(a+b)^5$系数:1,5,10,10,5,1
系数呈现杨辉三角特征,第$n$行($n\geq2$)第3项系数为$\frac{(n-1)(n-2)}{2}$。
对于$(a+b)^{12}$,$n=12$,第三项系数为$\frac{(12-1)(12-2)}{2}=\frac{11×10}{2}=55$。
C
11. 已知 $ m + n = m n $,则 $ ( m - 1 ) ( n - 1 ) = $
1
.答案:1
解析:
$(m - 1)(n - 1)$
$= mn - m - n + 1$
$= mn - (m + n) + 1$
因为$m + n = mn$,所以原式$= mn - mn + 1 = 1$
1
$= mn - m - n + 1$
$= mn - (m + n) + 1$
因为$m + n = mn$,所以原式$= mn - mn + 1 = 1$
1
12. 若 $ ( x - 7 ) ^ { 0 } = 1 $,则 $ x $ 的取值范围为
x≠7
.答案:x≠7
解析:
$x \neq 7$
13. 计算:$ 2 \sqrt { 3 } + \left| \frac { \sqrt { 3 } } { 2 } - 1 \right| = $
$1+\frac{3\sqrt{3}}{2}$
.答案:$1+\frac{3\sqrt{3}}{2}$
解析:
$2\sqrt{3}+\left(1-\frac{\sqrt{3}}{2}\right)$
$=2\sqrt{3}+1-\frac{\sqrt{3}}{2}$
$=1+\frac{3\sqrt{3}}{2}$
$=2\sqrt{3}+1-\frac{\sqrt{3}}{2}$
$=1+\frac{3\sqrt{3}}{2}$
14. 分解因式:$ 6 x y ^ { 2 } - 9 x ^ { 2 } y - y ^ { 3 } = $
$-y(3x-y)^2$
.答案:$-y(3x-y)^2$
15. 计算:$ ( - 3 ) ^ { 2025 } × \left( - \frac { 1 } { 3 } \right) ^ { 2023 } = $
9
.答案:9
解析:
$(-3)^{2025} × \left(-\frac{1}{3}\right)^{2023}$
$=(-3)^{2023} × (-3)^2 × \left(-\frac{1}{3}\right)^{2023}$
$=[(-3) × \left(-\frac{1}{3}\right)]^{2023} × 9$
$=1^{2023} × 9$
$=1 × 9$
$=9$
$=(-3)^{2023} × (-3)^2 × \left(-\frac{1}{3}\right)^{2023}$
$=[(-3) × \left(-\frac{1}{3}\right)]^{2023} × 9$
$=1^{2023} × 9$
$=1 × 9$
$=9$
16. 在 $ \mathrm { Rt } \triangle A B C $ 中,$ \angle C = 90 ^ { \circ } $,$ \angle B = 2 \angle A $,$ B C = \sqrt { 3 } \mathrm { cm } $,则 $ A B = $
$2\sqrt{3}$
$\mathrm { cm } $.答案:$2\sqrt{3}$
解析:
在$\mathrm { Rt } \triangle A B C$中,$\angle C = 90°$,则$\angle A + \angle B = 90°$。
因为$\angle B = 2\angle A$,所以$\angle A + 2\angle A = 90°$,$3\angle A = 90°$,解得$\angle A = 30°$。
在直角三角形中,$30°$角所对的直角边等于斜边的一半,$\angle A = 30°$,其对边为$BC = \sqrt{3}\ \mathrm{cm}$,所以斜边$AB = 2BC = 2\sqrt{3}\ \mathrm{cm}$。
$2\sqrt{3}$
因为$\angle B = 2\angle A$,所以$\angle A + 2\angle A = 90°$,$3\angle A = 90°$,解得$\angle A = 30°$。
在直角三角形中,$30°$角所对的直角边等于斜边的一半,$\angle A = 30°$,其对边为$BC = \sqrt{3}\ \mathrm{cm}$,所以斜边$AB = 2BC = 2\sqrt{3}\ \mathrm{cm}$。
$2\sqrt{3}$
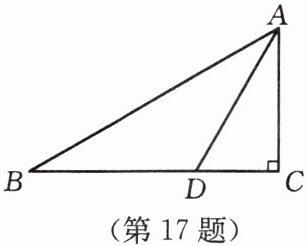
17. 如图,在 $ \triangle A B C $ 中,$ \angle C = 90 ^ { \circ } $,$ A D $ 平分 $ \angle B A C $,$ B C = 10 \mathrm { cm } $,$ B D = 7 \mathrm { cm } $,则点 $ D $ 到 $ A B $ 的距离为
3
$ \mathrm { cm } $.
答案:3
解析:
解:
∵ $ BC = 10 \, cm $, $ BD = 7 \, cm $,
∴ $ CD = BC - BD = 10 - 7 = 3 \, cm $.
∵ $ \angle C = 90° $,
∴ 点 $ D $ 到 $ AC $ 的距离为 $ CD = 3 \, cm $.
∵ $ AD $ 平分 $ \angle BAC $,
∴ 点 $ D $ 到 $ AB $ 的距离等于点 $ D $ 到 $ AC $ 的距离,即 $ 3 \, cm $.
3
∵ $ BC = 10 \, cm $, $ BD = 7 \, cm $,
∴ $ CD = BC - BD = 10 - 7 = 3 \, cm $.
∵ $ \angle C = 90° $,
∴ 点 $ D $ 到 $ AC $ 的距离为 $ CD = 3 \, cm $.
∵ $ AD $ 平分 $ \angle BAC $,
∴ 点 $ D $ 到 $ AB $ 的距离等于点 $ D $ 到 $ AC $ 的距离,即 $ 3 \, cm $.
3
18. 在平面直角坐标系 $ x O y $ 中,已知点 $ A ( 2 , - 2 ) $,在 $ y $ 轴上确定点 $ P $,使 $ \triangle A O P $ 为等腰三角形,则符合条件的点有
4
个.答案:4
解析:
设点$P(0,y)$,$O(0,0)$,$A(2,-2)$。
$OA=\sqrt{(2-0)^2+(-2-0)^2}=\sqrt{8}=2\sqrt{2}$,$OP=|y|$,$AP=\sqrt{(2-0)^2+(-2-y)^2}=\sqrt{4+(y+2)^2}$。
情况1:$OA=OP$,$|y|=2\sqrt{2}$,$y=2\sqrt{2}$或$y=-2\sqrt{2}$,得$P_1(0,2\sqrt{2})$,$P_2(0,-2\sqrt{2})$。
情况2:$OA=AP$,$\sqrt{4+(y+2)^2}=2\sqrt{2}$,$4+(y+2)^2=8$,$(y+2)^2=4$,$y+2=\pm2$,$y=0$或$y=-4$,$y=0$与$O$重合,舍去,得$P_3(0,-4)$。
情况3:$OP=AP$,$|y|=\sqrt{4+(y+2)^2}$,$y^2=4+y^2+4y+4$,$0=8+4y$,$y=-2$,得$P_4(0,-2)$。
符合条件的点有4个。
$OA=\sqrt{(2-0)^2+(-2-0)^2}=\sqrt{8}=2\sqrt{2}$,$OP=|y|$,$AP=\sqrt{(2-0)^2+(-2-y)^2}=\sqrt{4+(y+2)^2}$。
情况1:$OA=OP$,$|y|=2\sqrt{2}$,$y=2\sqrt{2}$或$y=-2\sqrt{2}$,得$P_1(0,2\sqrt{2})$,$P_2(0,-2\sqrt{2})$。
情况2:$OA=AP$,$\sqrt{4+(y+2)^2}=2\sqrt{2}$,$4+(y+2)^2=8$,$(y+2)^2=4$,$y+2=\pm2$,$y=0$或$y=-4$,$y=0$与$O$重合,舍去,得$P_3(0,-4)$。
情况3:$OP=AP$,$|y|=\sqrt{4+(y+2)^2}$,$y^2=4+y^2+4y+4$,$0=8+4y$,$y=-2$,得$P_4(0,-2)$。
符合条件的点有4个。
19. (10 分)计算:
(1)$ ( 5 a ^ { 2 } + 2 a ) - 4 ( 2 + 2 a ^ { 2 } ) $;
(2)$ \left( 1 + \frac { 4 } { x - 2 } \right) ÷ \frac { x + 2 } { x ^ { 2 } - 4 x + 4 } $.
(1)$ ( 5 a ^ { 2 } + 2 a ) - 4 ( 2 + 2 a ^ { 2 } ) $;
(2)$ \left( 1 + \frac { 4 } { x - 2 } \right) ÷ \frac { x + 2 } { x ^ { 2 } - 4 x + 4 } $.
答案:$(1) -3a^2+2a-8; (2) x-2$
解析:
(1) $(5a^{2}+2a)-4(2+2a^{2})$
$=5a^{2}+2a - 8 - 8a^{2}$
$=-3a^{2}+2a - 8$
(2) $\left(1 + \frac{4}{x - 2}\right)÷\frac{x + 2}{x^{2}-4x + 4}$
$=\left(\frac{x - 2}{x - 2}+\frac{4}{x - 2}\right)÷\frac{x + 2}{(x - 2)^{2}}$
$=\frac{x + 2}{x - 2}×\frac{(x - 2)^{2}}{x + 2}$
$=x - 2$
20. (10 分)用乘法公式计算:
(1)$ 59.8 × 60.2 $;
(2)$ 198 ^ { 2 } $.
(1)$ 59.8 × 60.2 $;
(2)$ 198 ^ { 2 } $.
答案:
(1) 3599.96;
(2) 39204
(1) 3599.96;
(2) 39204