1. 过△ABC 的顶点 A,作 BC 边上的高,以下作法正确的是(
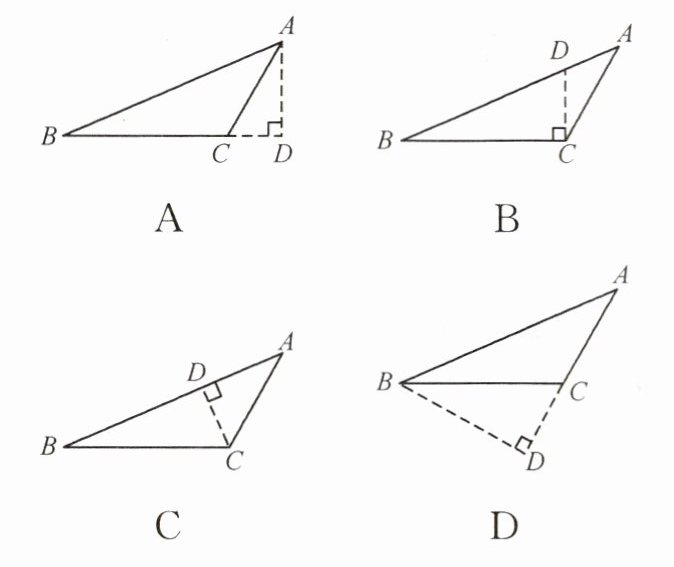
A
)
答案:A
2. 下列各式从左往右计算正确的是(
A.$ a - ( b + c ) = a - b + c $
B.$ x ^ { 2 } - 4 = ( x - 2 ) ^ { 2 } $
C.$ ( a - b ) ( a + c ) = a ^ { 2 } - a b + a c - b c $
D.$ ( - x ) ^ { 3 } ÷ x ^ { 3 } = x $($ x \neq 0 $)
C
)A.$ a - ( b + c ) = a - b + c $
B.$ x ^ { 2 } - 4 = ( x - 2 ) ^ { 2 } $
C.$ ( a - b ) ( a + c ) = a ^ { 2 } - a b + a c - b c $
D.$ ( - x ) ^ { 3 } ÷ x ^ { 3 } = x $($ x \neq 0 $)
答案:C
解析:
A. $a - (b + c) = a - b - c$,故A错误;
B. $x^2 - 4 = (x - 2)(x + 2)$,故B错误;
C. $(a - b)(a + c) = a^2 + ac - ab - bc$,故C正确;
D. $(-x)^3 ÷ x^3 = -x^3 ÷ x^3 = -1$,故D错误。
C
B. $x^2 - 4 = (x - 2)(x + 2)$,故B错误;
C. $(a - b)(a + c) = a^2 + ac - ab - bc$,故C正确;
D. $(-x)^3 ÷ x^3 = -x^3 ÷ x^3 = -1$,故D错误。
C
3. 如图,在 $ 4 × 4 $ 的正方形网格中,已有四个小正方形被涂黑. 若将图中其余小正方形任意涂黑一个,使整个图案构成一个轴对称图形,则该小正方形的位置可以是(

A.(1,2)
B.(2,4)
C.(3,2)
D.(4,4)
B
)
A.(1,2)
B.(2,4)
C.(3,2)
D.(4,4)
答案:B
4. 如果把 $ \frac { 5 x } { x + y } $ 中的 $ x $ 与 $ y $ 都扩大 10 倍,那么这个代数式的值(
A.不变
B.扩大 50 倍
C.扩大 10 倍
D.缩小为原来的 $ \frac { 1 } { 10 } $
A
)A.不变
B.扩大 50 倍
C.扩大 10 倍
D.缩小为原来的 $ \frac { 1 } { 10 } $
答案:A
解析:
将$x$与$y$都扩大10倍,原代数式变为$\frac{5×10x}{10x+10y}$。
化简得:$\frac{50x}{10(x+y)}=\frac{5x}{x+y}$。
与原代数式值相等,所以这个代数式的值不变。
A
化简得:$\frac{50x}{10(x+y)}=\frac{5x}{x+y}$。
与原代数式值相等,所以这个代数式的值不变。
A
5. 下列命题中不正确的是(
A.关于直线对称的两个三角形一定全等
B.角是轴对称图形
C.等边三角形有 3 条对称轴
D.等腰三角形一边上的高、中线及这边所对角的角平分线重合
D
)A.关于直线对称的两个三角形一定全等
B.角是轴对称图形
C.等边三角形有 3 条对称轴
D.等腰三角形一边上的高、中线及这边所对角的角平分线重合
答案:D
6. 等腰三角形的一个内角是 $ 50 ^ { \circ } $,则这个三角形的底角的大小是(
A.$ 65 ^ { \circ } $或 $ 50 ^ { \circ } $
B.$ 80 ^ { \circ } $或 $ 40 ^ { \circ } $
C.$ 65 ^ { \circ } $或 $ 80 ^ { \circ } $
D.$ 50 ^ { \circ } $或 $ 80 ^ { \circ } $
A
)A.$ 65 ^ { \circ } $或 $ 50 ^ { \circ } $
B.$ 80 ^ { \circ } $或 $ 40 ^ { \circ } $
C.$ 65 ^ { \circ } $或 $ 80 ^ { \circ } $
D.$ 50 ^ { \circ } $或 $ 80 ^ { \circ } $
答案:A
解析:
当$50^{\circ}$角为顶角时,底角为$\frac{180^{\circ}-50^{\circ}}{2}=65^{\circ}$;当$50^{\circ}$角为底角时,底角为$50^{\circ}$。这个三角形的底角的大小是$65^{\circ}$或$50^{\circ}$。
A
A
7. 到三角形三个顶点的距离都相等的点是这个三角形的(
A.三条高的交点
B.三条角平分线的交点
C.三条中线的交点
D.三条边的垂直平分线的交点
D
)A.三条高的交点
B.三条角平分线的交点
C.三条中线的交点
D.三条边的垂直平分线的交点
答案:D
8. 化简 $ \frac { a } { b } - \frac { b } { a } - \frac { a ^ { 2 } + b ^ { 2 } } { a b } $ 的结果是(
A.0
B.$ - \frac { 2 a } { b } $
C.$ - \frac { 2 b } { a } $
D.$ \frac { 2 b } { a } $
C
)A.0
B.$ - \frac { 2 a } { b } $
C.$ - \frac { 2 b } { a } $
D.$ \frac { 2 b } { a } $
答案:C
解析:
$\begin{aligned}\frac{a}{b} - \frac{b}{a} - \frac{a^2 + b^2}{ab}&=\frac{a^2}{ab} - \frac{b^2}{ab} - \frac{a^2 + b^2}{ab}\\&=\frac{a^2 - b^2 - (a^2 + b^2)}{ab}\\&=\frac{a^2 - b^2 - a^2 - b^2}{ab}\\&=\frac{-2b^2}{ab}\\&=-\frac{2b}{a}\end{aligned}$
C
C