2. 如图,$AD = AE$,$BE = CD$,$\angle 1= \angle 2 = 110^{\circ}$,$\angle BAE = 60^{\circ}$。那么下列结论中错误的是(
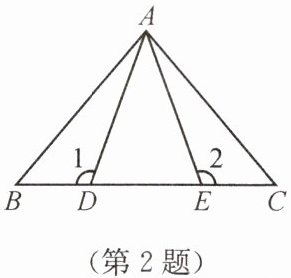
A.$\triangle ABE\cong\triangle ACD$
B.$\triangle ABD\cong\triangle ACE$
C.$\angle ACE = 30^{\circ}$
D.$AB = AC$
C
)
A.$\triangle ABE\cong\triangle ACD$
B.$\triangle ABD\cong\triangle ACE$
C.$\angle ACE = 30^{\circ}$
D.$AB = AC$
答案:C
解析:
证明:
∵∠1=∠2=110°,
∴∠ADC=∠AEB=70°。
∵BE=CD,AD=AE,
∴△ABE≌△ACD(AAS),故A正确。
∴AB=AC,∠BAE=∠CAD=60°,故D正确。
∵AD=AE,
∴∠ADE=∠AED=(180°-∠DAE)/2。
∵∠BAC=∠BAE+∠EAD=∠CAD+∠EAD,
∴∠BAC=∠BAE+∠CAD-∠EAD=60°+60°-∠EAD=120°-∠EAD。
又
∵AB=AC,
∴∠ABC=∠ACB=(180°-∠BAC)/2=(180°-120°+∠EAD)/2=30°+∠EAD/2。
∵∠1=∠ABC+∠BAD=110°,∠BAD=∠BAE-∠DAE=60°-∠EAD,
∴∠ABC+60°-∠EAD=110°,即30°+∠EAD/2+60°-∠EAD=110°,
解得∠EAD= -40°(矛盾),说明△ABD≌△ACE不成立,故B错误。
∵△ABE≌△ACD,
∴∠ABE=∠ACD。
∵∠2=∠ABC+∠BEC=110°,∠BEC=∠AEB-∠AED=70°-∠AED,
∠AED=(180°-∠EAD)/2=(180°+40°)/2=110°,
∴∠BEC=70°-110°=-40°(矛盾),故∠ACE=∠ACB-∠BCE≠30°,故C错误。
综上,错误的是C。
答案:C
∵∠1=∠2=110°,
∴∠ADC=∠AEB=70°。
∵BE=CD,AD=AE,
∴△ABE≌△ACD(AAS),故A正确。
∴AB=AC,∠BAE=∠CAD=60°,故D正确。
∵AD=AE,
∴∠ADE=∠AED=(180°-∠DAE)/2。
∵∠BAC=∠BAE+∠EAD=∠CAD+∠EAD,
∴∠BAC=∠BAE+∠CAD-∠EAD=60°+60°-∠EAD=120°-∠EAD。
又
∵AB=AC,
∴∠ABC=∠ACB=(180°-∠BAC)/2=(180°-120°+∠EAD)/2=30°+∠EAD/2。
∵∠1=∠ABC+∠BAD=110°,∠BAD=∠BAE-∠DAE=60°-∠EAD,
∴∠ABC+60°-∠EAD=110°,即30°+∠EAD/2+60°-∠EAD=110°,
解得∠EAD= -40°(矛盾),说明△ABD≌△ACE不成立,故B错误。
∵△ABE≌△ACD,
∴∠ABE=∠ACD。
∵∠2=∠ABC+∠BEC=110°,∠BEC=∠AEB-∠AED=70°-∠AED,
∠AED=(180°-∠EAD)/2=(180°+40°)/2=110°,
∴∠BEC=70°-110°=-40°(矛盾),故∠ACE=∠ACB-∠BCE≠30°,故C错误。
综上,错误的是C。
答案:C
3. 如图,点$E$,$F在AC$上,$AD = BC$,$DF = BE$,要使$\triangle ADF\cong\triangle CBE$,还需要添加的一个条件是(
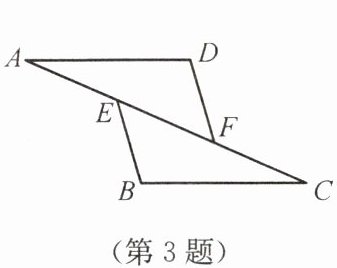
A.$\angle A= \angle C$
B.$\angle D= \angle B$
C.$AD// BC$
D.$DF// BE$
B
)
A.$\angle A= \angle C$
B.$\angle D= \angle B$
C.$AD// BC$
D.$DF// BE$
答案:B
解析:
要使$\triangle ADF\cong\triangle CBE$,已知$AD = BC$,$DF = BE$。
若添加条件$\angle D= \angle B$,则在$\triangle ADF$和$\triangle CBE$中,有:
$\begin{cases}AD = BC \\\angle D = \angle B \\DF = BE\end{cases}$
根据“SAS”(边角边)全等判定定理,可得$\triangle ADF\cong\triangle CBE$。
B
若添加条件$\angle D= \angle B$,则在$\triangle ADF$和$\triangle CBE$中,有:
$\begin{cases}AD = BC \\\angle D = \angle B \\DF = BE\end{cases}$
根据“SAS”(边角边)全等判定定理,可得$\triangle ADF\cong\triangle CBE$。
B
4. 已知$\triangle ABC\cong\triangle DEF$,$BC = EF = 9\ cm$,$\triangle ABC的面积是18\ cm^{2}$,则$EF$边上的高是
4
$cm$。答案:4
解析:
因为$\triangle ABC\cong\triangle DEF$,所以$\triangle DEF$的面积等于$\triangle ABC$的面积,即$18\ cm^2$。设$EF$边上的高为$h\ cm$,根据三角形面积公式$S = \frac{1}{2} × 底 × 高$,可得$\frac{1}{2} × EF × h = 18$。已知$EF = 9\ cm$,则$\frac{1}{2} × 9 × h = 18$,解得$h = 4$。
4
4
5. 如图,已知$OA = OC$,$OB = OD$,$\angle AOC= \angle BOD$。求证:$\triangle AOB\cong\triangle COD$。
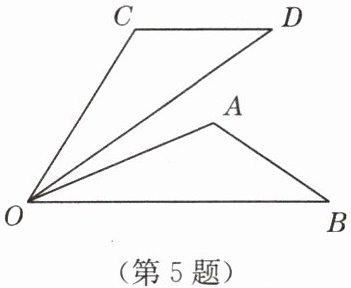

答案:证明:
∵∠AOC=∠BOD,
∴∠AOC - ∠AOD=∠BOD - ∠AOD,即∠COD=∠AOB.在△AOB和△COD中,$\left\{\begin{array}{l} OA=OC,\\ ∠AOB=∠COD,\\ OB=OD,\end{array}\right. \therefore \triangle AOB\cong \triangle COD(SAS).$
∵∠AOC=∠BOD,
∴∠AOC - ∠AOD=∠BOD - ∠AOD,即∠COD=∠AOB.在△AOB和△COD中,$\left\{\begin{array}{l} OA=OC,\\ ∠AOB=∠COD,\\ OB=OD,\end{array}\right. \therefore \triangle AOB\cong \triangle COD(SAS).$
6. 如图,点$B$,$E$,$C$,$F$在同一条直线上,$AB = DE$,$AB// DE$,$BE = CF$。
(1)求证:$AC// DF$;
(2)若$BF = 13$,$EC = 5$,求$BC$的长。
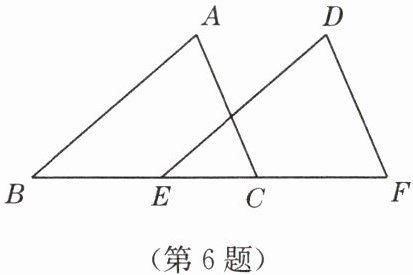
(1)求证:$AC// DF$;
(2)若$BF = 13$,$EC = 5$,求$BC$的长。

答案:(2) 9
解析:
(1) 证明:
∵AB//DE,
∴∠B=∠DEF。
∵BE=CF,
∴BE+EC=CF+EC,即BC=EF。
在△ABC和△DEF中,
$\left\{\begin{array}{l} AB=DE,\\ ∠B=∠DEF,\\ BC=EF,\end{array}\right.$
∴△ABC≌△DEF(SAS)。
∴∠ACB=∠F。
∴AC//DF。
(2) ∵BF=13,EC=5,
∴BE+CF=BF-EC=13-5=8。
∵BE=CF,
∴BE=CF=4。
∴BC=BE+EC=4+5=9。
∵AB//DE,
∴∠B=∠DEF。
∵BE=CF,
∴BE+EC=CF+EC,即BC=EF。
在△ABC和△DEF中,
$\left\{\begin{array}{l} AB=DE,\\ ∠B=∠DEF,\\ BC=EF,\end{array}\right.$
∴△ABC≌△DEF(SAS)。
∴∠ACB=∠F。
∴AC//DF。
(2) ∵BF=13,EC=5,
∴BE+CF=BF-EC=13-5=8。
∵BE=CF,
∴BE=CF=4。
∴BC=BE+EC=4+5=9。
7. 如图,点$C$,$F$,$E$,$B$在同一条直线上,$\angle CFD= \angle BEA$,$CE = BF$,$DF = AE$,请写出$CD与AB$之间的关系,并证明你的结论。
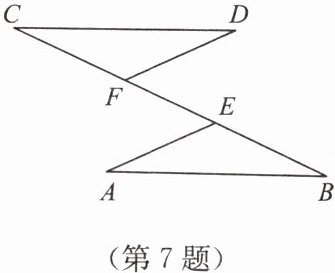

答案:结论:CD//AB,CD=AB.理由:
∵CE=BF,
∴CE - EF=BF - EF,
∴CF=BE.在△CFD和△BEA中,$\left\{\begin{array}{l} CF=BE,\\ ∠CFD=∠BEA,\\ DF=AE,\end{array}\right. \therefore \triangle CFD\cong \triangle BEA(SAS),\therefore CD=AB,∠C=∠B,\therefore CD//AB.$
∵CE=BF,
∴CE - EF=BF - EF,
∴CF=BE.在△CFD和△BEA中,$\left\{\begin{array}{l} CF=BE,\\ ∠CFD=∠BEA,\\ DF=AE,\end{array}\right. \therefore \triangle CFD\cong \triangle BEA(SAS),\therefore CD=AB,∠C=∠B,\therefore CD//AB.$