1. 如果一个三角形的两边和它们的
夹角
确定了,那么这个三角形的形状和大小就确定了。答案:夹角
2. 两边和它们的
夹
角分别相等
的两个三角形全等(可以简写成“边角边
”或“SAS
”)。答案:夹;分别相等;边角边;SAS
3. 两边和其中一边的对角分别相等的两个三角形
不一定
全等(选填“一定”或“不一定”)。答案:不一定
4. 如图,$OA = OB$,$OC = OD$,$\angle O = 50^{\circ}$,$\angle D = 35^{\circ}$,则$\angle AEC= $
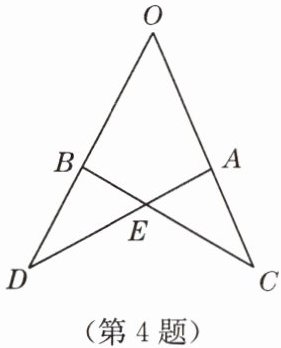
60°
。 
答案:60°
解析:
证明:在△OAD和△OBC中,
∵OA=OB,∠O=∠O,OD=OC,
∴△OAD≌△OBC(SAS),
∴∠C=∠D=35°。
在△OAD中,∠OAD=180°-∠O-∠D=180°-50°-35°=95°。
在△AEC中,∠AEC=180°-∠EAC-∠C=180°-(180°-∠OAD)-∠C=∠OAD-∠C=95°-35°=60°。
60°
∵OA=OB,∠O=∠O,OD=OC,
∴△OAD≌△OBC(SAS),
∴∠C=∠D=35°。
在△OAD中,∠OAD=180°-∠O-∠D=180°-50°-35°=95°。
在△AEC中,∠AEC=180°-∠EAC-∠C=180°-(180°-∠OAD)-∠C=∠OAD-∠C=95°-35°=60°。
60°
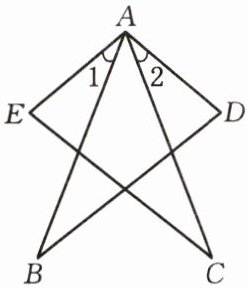
问题 如图,$AB = AC$,$AD = AE$,$\angle 1= \angle 2$。求证:$BD = CE$。
名师指导
要证明$BD = CE$,可证明$\triangle ABD\cong\triangle ACE$。
解题示范(学生在教师指导下,独立完成)
证明:
名师指导
要证明$BD = CE$,可证明$\triangle ABD\cong\triangle ACE$。
解题示范(学生在教师指导下,独立完成)
证明:

答案:证明:
已知 $\angle 1 = \angle 2$,
因此$\angle BAD = \angle EAC$(因为$\angle BAD=\angle 1+\angle CAD$,$\angle EAC=\angle 2+\angle CAD$)。
在 $\triangle ABD$ 和 $\triangle ACE$ 中:
$AB = AC$(已知),
$\angle BAD = \angle EAC$(已证),
$AD = AE$(已知)。
因此,$\triangle ABD \cong \triangle ACE$(SAS)。
所以$BD = CE$。
已知 $\angle 1 = \angle 2$,
因此$\angle BAD = \angle EAC$(因为$\angle BAD=\angle 1+\angle CAD$,$\angle EAC=\angle 2+\angle CAD$)。
在 $\triangle ABD$ 和 $\triangle ACE$ 中:
$AB = AC$(已知),
$\angle BAD = \angle EAC$(已证),
$AD = AE$(已知)。
因此,$\triangle ABD \cong \triangle ACE$(SAS)。
所以$BD = CE$。
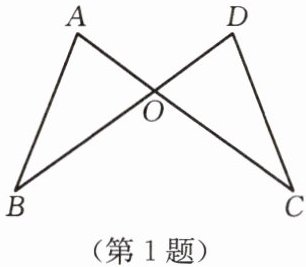
1. 如图,$BD$,$AC相交于点O$,且$OA = OD$,用“SAS”得到$\triangle AOB\cong\triangle DOC$,还需(
A.$AB = DC$
B.$OB = OC$
C.$\angle A= \angle D$
D.$\angle AOB= \angle DOC$
B
)
A.$AB = DC$
B.$OB = OC$
C.$\angle A= \angle D$
D.$\angle AOB= \angle DOC$
答案:B
解析:
证明:要使用“SAS”判定$\triangle AOB\cong\triangle DOC$,已知$OA = OD$,且$\angle AOB$与$\angle DOC$是对顶角,所以$\angle AOB = \angle DOC$(对顶角相等)。此时已有一组边和一组角对应相等,根据“SAS”(两边及其夹角对应相等的两个三角形全等),还需夹$\angle AOB$和$\angle DOC$的另一组边对应相等,即$OB = OC$。
B
B