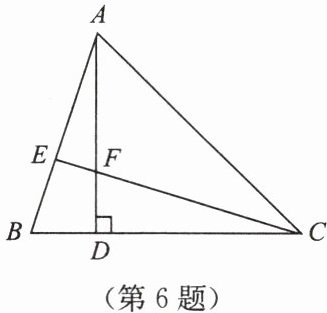
6. 如图,已知$AD \perp BC于点D$,$\triangle ABD \cong \triangle CFD$.
(1)求证:$CE \perp AB$;
(2)若$BC = 7$,$AD = 5$,求$AF$的长.
]
(1)求证:$CE \perp AB$;
(2)若$BC = 7$,$AD = 5$,求$AF$的长.
]

答案:(1)证明:因为△ABD≌△CFD,所以∠BAD=∠FCD. 又因为∠AFE=∠CFD,所以∠AEF=∠CDF=90°,所以CE⊥AB. (2)AF=3.
解析:
(1)证明:
∵△ABD≌△CFD,
∴∠BAD=∠FCD。
∵∠AFE=∠CFD,
∴∠AEF=∠CDF。
∵AD⊥BC,
∴∠CDF=90°,
∴∠AEF=90°,
∴CE⊥AB。
(2)
∵△ABD≌△CFD,
∴AD=CD=5。
∵BC=7,
∴BD=BC-CD=7-5=2。
∵AD=5,BD=2,
∴AF=AD-DF=AD-BD=5-2=3。
故AF=3。
∵△ABD≌△CFD,
∴∠BAD=∠FCD。
∵∠AFE=∠CFD,
∴∠AEF=∠CDF。
∵AD⊥BC,
∴∠CDF=90°,
∴∠AEF=90°,
∴CE⊥AB。
(2)
∵△ABD≌△CFD,
∴AD=CD=5。
∵BC=7,
∴BD=BC-CD=7-5=2。
∵AD=5,BD=2,
∴AF=AD-DF=AD-BD=5-2=3。
故AF=3。
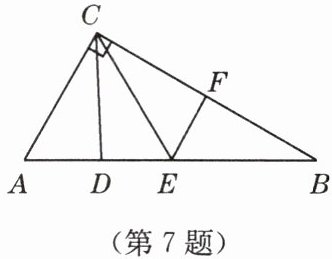
7. 如图,在$\triangle ABC$中,$\angle ACB = 90^{\circ}$,$\triangle CAD \cong \triangle CED$,$\triangle CEF \cong \triangle BEF$,$\triangle CEF \cong \triangle CAD$.
(1)求$\angle B$的度数;
(2)求证:$EF // AC$.
]
(1)求$\angle B$的度数;
(2)求证:$EF // AC$.
]

答案:(1)30°;(2)提示:证∠BFE=90°=∠ACB.
解析:
(1)解:设∠B=x,
∵△CEF≌△BEF,
∴∠ECB=∠B=x,∠CEF=∠BEF,∠CFE=∠BFE,
∵△CAD≌△CED≌△CEF,
∴∠A=∠CED=∠CEF,∠ACD=∠ECD=∠ECF,∠ADC=∠CDE=∠CFE,
∵∠ACB=90°,
∴∠ACD+∠ECD+∠ECF=90°,
∴∠ACD=∠ECD=∠ECF=30°,
∵∠ECB=x,∠ACB=90°,
∴∠ACE=90°-x,
∵∠ACE=∠ACD+∠ECD=60°,
∴90°-x=60°,
解得x=30°,即∠B=30°.
(2)证明:由(1)知∠B=30°,∠CFE=∠BFE,
∵∠CFE+∠BFE=180°,
∴∠BFE=90°,
∵∠ACB=90°,
∴∠BFE=∠ACB,
∴EF//AC.
∵△CEF≌△BEF,
∴∠ECB=∠B=x,∠CEF=∠BEF,∠CFE=∠BFE,
∵△CAD≌△CED≌△CEF,
∴∠A=∠CED=∠CEF,∠ACD=∠ECD=∠ECF,∠ADC=∠CDE=∠CFE,
∵∠ACB=90°,
∴∠ACD+∠ECD+∠ECF=90°,
∴∠ACD=∠ECD=∠ECF=30°,
∵∠ECB=x,∠ACB=90°,
∴∠ACE=90°-x,
∵∠ACE=∠ACD+∠ECD=60°,
∴90°-x=60°,
解得x=30°,即∠B=30°.
(2)证明:由(1)知∠B=30°,∠CFE=∠BFE,
∵∠CFE+∠BFE=180°,
∴∠BFE=90°,
∵∠ACB=90°,
∴∠BFE=∠ACB,
∴EF//AC.
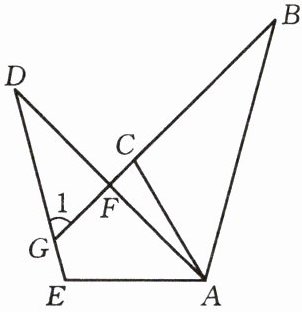
如图,已知$\triangle ABC \cong \triangle ADE$,$AB = AD$,$AC = AE$,$BC的延长线交DA于点F$,交$DE于点G$,$\angle AED = 105^{\circ}$,$\angle CAD = 15^{\circ}$,$\angle B = 30^{\circ}$,求$\angle 1$的度数.
]
]

答案:∠1=60°.
解析:
证明:
∵$\triangle ABC \cong \triangle ADE$,
∴$\angle AED = \angle ACB = 105°$,$\angle D = \angle B = 30°$。
在$\triangle ABC$中,
$\angle BAC = 180° - \angle B - \angle ACB = 180° - 30° - 105° = 45°$。
∵$\angle CAD = 15°$,
∴$\angle DAF = \angle BAC - \angle CAD = 45° - 15° = 30°$。
在$\triangle DFG$中,
$\angle AFD = 180° - \angle D - \angle DAF = 180° - 30° - 30° = 120°$。
∵$\angle AFD + \angle GFD = 180°$,
∴$\angle GFD = 180° - 120° = 60°$,即$\angle 1 = 60°$。
$\angle 1 = 60°$。
∵$\triangle ABC \cong \triangle ADE$,
∴$\angle AED = \angle ACB = 105°$,$\angle D = \angle B = 30°$。
在$\triangle ABC$中,
$\angle BAC = 180° - \angle B - \angle ACB = 180° - 30° - 105° = 45°$。
∵$\angle CAD = 15°$,
∴$\angle DAF = \angle BAC - \angle CAD = 45° - 15° = 30°$。
在$\triangle DFG$中,
$\angle AFD = 180° - \angle D - \angle DAF = 180° - 30° - 30° = 120°$。
∵$\angle AFD + \angle GFD = 180°$,
∴$\angle GFD = 180° - 120° = 60°$,即$\angle 1 = 60°$。
$\angle 1 = 60°$。