1. 下列说法不正确的是(
A.如果两个图形全等,那么它们的形状和大小一定相同
B.面积相等的两个图形是全等图形
C.图形全等,只与形状、大小有关,而与它们的位置无关
D.形状相同的两个图形不一定全等
B
)A.如果两个图形全等,那么它们的形状和大小一定相同
B.面积相等的两个图形是全等图形
C.图形全等,只与形状、大小有关,而与它们的位置无关
D.形状相同的两个图形不一定全等
答案:B
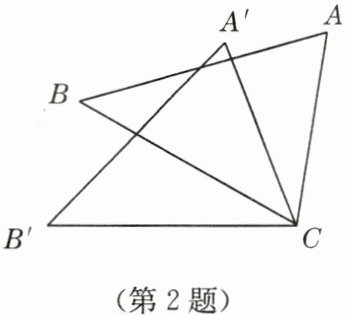
2. 如图,已知$\triangle ACB \cong \triangle A'CB'$,$\angle ACB = 70^{\circ}$,$\angle ACB' = 100^{\circ}$,则$\angle BCA'$的度数为(
A.$40^{\circ}$
B.$45^{\circ}$
C.$50^{\circ}$
D.$55^{\circ}$
]
A
)
A.$40^{\circ}$
B.$45^{\circ}$
C.$50^{\circ}$
D.$55^{\circ}$
]
答案:A
解析:
证明:
∵$\triangle ACB \cong \triangle A'CB'$,
∴$\angle A'CB' = \angle ACB = 70°$。
设$\angle BCA' = x$,
∵$\angle ACB' = 100°$,
∴$\angle ACB' = \angle ACB + \angle B'CB = 100°$,
即$70° + \angle B'CB = 100°$,
解得$\angle B'CB = 30°$。
又
∵$\angle A'CB' = \angle BCA' + \angle B'CB$,
∴$70° = x + 30°$,
解得$x = 40°$。
故$\angle BCA' = 40°$。
A
∵$\triangle ACB \cong \triangle A'CB'$,
∴$\angle A'CB' = \angle ACB = 70°$。
设$\angle BCA' = x$,
∵$\angle ACB' = 100°$,
∴$\angle ACB' = \angle ACB + \angle B'CB = 100°$,
即$70° + \angle B'CB = 100°$,
解得$\angle B'CB = 30°$。
又
∵$\angle A'CB' = \angle BCA' + \angle B'CB$,
∴$70° = x + 30°$,
解得$x = 40°$。
故$\angle BCA' = 40°$。
A
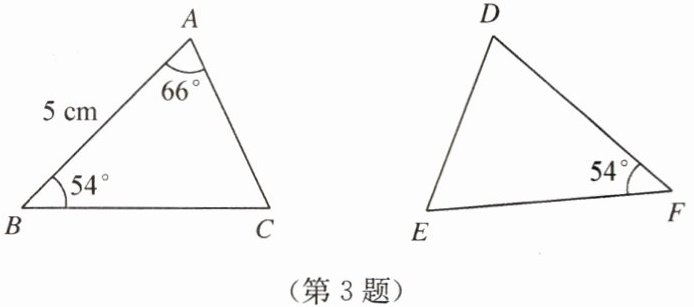
3. 如图,若$\triangle ABC与\triangle DEF$全等,且$BC = DF$,则下列结论正确的是(
A.$\angle D = 66^{\circ}$
B.$EF = 5\mathrm{cm}$
C.$\angle E = 60^{\circ}$
D.$DE = 5\mathrm{cm}$
]
B
)
A.$\angle D = 66^{\circ}$
B.$EF = 5\mathrm{cm}$
C.$\angle E = 60^{\circ}$
D.$DE = 5\mathrm{cm}$
]
答案:B
解析:
在$\triangle ABC$中,$\angle A=66°$,$\angle B=54°$,则$\angle C=180° - 66° - 54°=60°$,$AB=5\mathrm{cm}$。
因为$\triangle ABC$与$\triangle DEF$全等,且$BC = DF$,所以$BC$与$DF$是对应边。
当$\triangle ABC\cong\triangle DFE$时,$AB=DF$,$BC=FE$,$AC=DE$,$\angle A=\angle D$,$\angle B=\angle F$,$\angle C=\angle E$。已知$\angle B=54°$,所以$\angle F=54°$,符合对应关系,此时$AB=DF=5\mathrm{cm}$,$BC=EF$,即$EF=BC$,但题目未给出$BC$长度,无法直接得出$EF=5\mathrm{cm}$;$\angle D=\angle A=66°$,$\angle E=\angle C=60°$,$DE=AC$,$AC$长度未知,无法得出$DE=5\mathrm{cm}$。
当$\triangle ABC\cong\triangle FDE$时,$AB=FD$,$BC=DE$,$AC=FE$,$\angle A=\angle F$,$\angle B=\angle D$,$\angle C=\angle E$。已知$\angle B=54°$,则$\angle D=54°$,$\angle F=\angle A=66°$,与已知$\angle F=54°$矛盾,此情况不成立。
综上,只有$\angle E=\angle C=60°$一定成立。
C
因为$\triangle ABC$与$\triangle DEF$全等,且$BC = DF$,所以$BC$与$DF$是对应边。
当$\triangle ABC\cong\triangle DFE$时,$AB=DF$,$BC=FE$,$AC=DE$,$\angle A=\angle D$,$\angle B=\angle F$,$\angle C=\angle E$。已知$\angle B=54°$,所以$\angle F=54°$,符合对应关系,此时$AB=DF=5\mathrm{cm}$,$BC=EF$,即$EF=BC$,但题目未给出$BC$长度,无法直接得出$EF=5\mathrm{cm}$;$\angle D=\angle A=66°$,$\angle E=\angle C=60°$,$DE=AC$,$AC$长度未知,无法得出$DE=5\mathrm{cm}$。
当$\triangle ABC\cong\triangle FDE$时,$AB=FD$,$BC=DE$,$AC=FE$,$\angle A=\angle F$,$\angle B=\angle D$,$\angle C=\angle E$。已知$\angle B=54°$,则$\angle D=54°$,$\angle F=\angle A=66°$,与已知$\angle F=54°$矛盾,此情况不成立。
综上,只有$\angle E=\angle C=60°$一定成立。
C
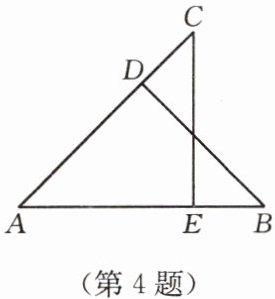
4. 如图,已知$\triangle ABD \cong \triangle ACE$,点$B和点C$是对应点,$AB = 6\mathrm{cm}$,$BD = 5\mathrm{cm}$,$AD = 4\mathrm{cm}$,则$BE$的长是
2 cm
.
答案:2 cm
解析:
解:
∵△ABD≌△ACE,点B和点C是对应点,
∴AB=AC,AD=AE。
∵AD=4cm,
∴AE=4cm。
∵AB=6cm,
∴BE=AB - AE=6 - 4=2cm。
故答案为:2 cm。
∵△ABD≌△ACE,点B和点C是对应点,
∴AB=AC,AD=AE。
∵AD=4cm,
∴AE=4cm。
∵AB=6cm,
∴BE=AB - AE=6 - 4=2cm。
故答案为:2 cm。
5. 已知$\triangle ABC$的边长均为整数,且最大边的边长为$4$,那么符合条件的不全等的三角形最多有
6
个.答案:6
解析:
设三角形的三边长分别为$a$、$b$、$c$,且$a \leq b \leq c$,$c = 4$,$a$、$b$、$c$为整数。
根据三角形三边关系:$a + b > c$。
情况1:$b = 4$
$a = 1$:$1 + 4 > 4$,成立,三角形(1,4,4)
$a = 2$:$2 + 4 > 4$,成立,三角形(2,4,4)
$a = 3$:$3 + 4 > 4$,成立,三角形(3,4,4)
$a = 4$:$4 + 4 > 4$,成立,三角形(4,4,4)
情况2:$b = 3$
$a = 2$:$2 + 3 > 4$,成立,三角形(2,3,4)
$a = 3$:$3 + 3 > 4$,成立,三角形(3,3,4)
情况3:$b = 2$
$a = 2$:$2 + 2 = 4$,不成立
综上,符合条件的不全等三角形有(1,4,4)、(2,4,4)、(3,4,4)、(4,4,4)、(2,3,4)、(3,3,4),共6个。
6
根据三角形三边关系:$a + b > c$。
情况1:$b = 4$
$a = 1$:$1 + 4 > 4$,成立,三角形(1,4,4)
$a = 2$:$2 + 4 > 4$,成立,三角形(2,4,4)
$a = 3$:$3 + 4 > 4$,成立,三角形(3,4,4)
$a = 4$:$4 + 4 > 4$,成立,三角形(4,4,4)
情况2:$b = 3$
$a = 2$:$2 + 3 > 4$,成立,三角形(2,3,4)
$a = 3$:$3 + 3 > 4$,成立,三角形(3,3,4)
情况3:$b = 2$
$a = 2$:$2 + 2 = 4$,不成立
综上,符合条件的不全等三角形有(1,4,4)、(2,4,4)、(3,4,4)、(4,4,4)、(2,3,4)、(3,3,4),共6个。
6