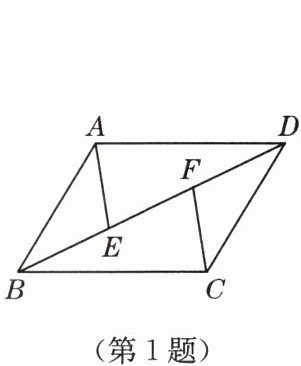
1. 如图,$AB// CD$,$AD// BC$,$E$,$F是BD$上两点,且$BF = DE$,则图中共有全等三角形(
A.$1$对
B.$2$对
C.$3$对
D.$4$对
C
)
A.$1$对
B.$2$对
C.$3$对
D.$4$对
答案:C
解析:
证明:
∵ $AB // CD$,$AD // BC$,
∴ 四边形 $ABCD$ 是平行四边形,
∴ $AB = CD$,$AD = BC$,$\angle ABD = \angle CDB$,$\angle ADB = \angle CBD$。
1. 在 $\triangle ABD$ 和 $\triangle CDB$ 中,
$\begin{cases} AB = CD \\ \angle ABD = \angle CDB \\ BD = DB \end{cases}$,
∴ $\triangle ABD \cong \triangle CDB$(SAS)。
2.
∵ $BF = DE$,
∴ $BE = BD - DE = BD - BF = DF$。
在 $\triangle ABE$ 和 $\triangle CDF$ 中,
$\begin{cases} AB = CD \\ \angle ABE = \angle CDF \\ BE = DF \end{cases}$,
∴ $\triangle ABE \cong \triangle CDF$(SAS)。
3. 在 $\triangle ADE$ 和 $\triangle CBF$ 中,
$\begin{cases} AD = CB \\ \angle ADE = \angle CBF \\ DE = BF \end{cases}$,
∴ $\triangle ADE \cong \triangle CBF$(SAS)。
综上,共有 3 对全等三角形。
答案:C
∵ $AB // CD$,$AD // BC$,
∴ 四边形 $ABCD$ 是平行四边形,
∴ $AB = CD$,$AD = BC$,$\angle ABD = \angle CDB$,$\angle ADB = \angle CBD$。
1. 在 $\triangle ABD$ 和 $\triangle CDB$ 中,
$\begin{cases} AB = CD \\ \angle ABD = \angle CDB \\ BD = DB \end{cases}$,
∴ $\triangle ABD \cong \triangle CDB$(SAS)。
2.
∵ $BF = DE$,
∴ $BE = BD - DE = BD - BF = DF$。
在 $\triangle ABE$ 和 $\triangle CDF$ 中,
$\begin{cases} AB = CD \\ \angle ABE = \angle CDF \\ BE = DF \end{cases}$,
∴ $\triangle ABE \cong \triangle CDF$(SAS)。
3. 在 $\triangle ADE$ 和 $\triangle CBF$ 中,
$\begin{cases} AD = CB \\ \angle ADE = \angle CBF \\ DE = BF \end{cases}$,
∴ $\triangle ADE \cong \triangle CBF$(SAS)。
综上,共有 3 对全等三角形。
答案:C
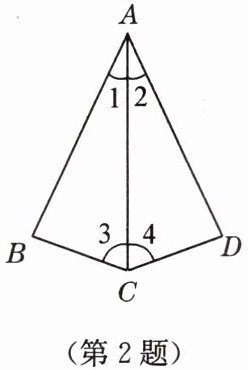
2. 如图,已知$\angle 1= \angle 2$,添加一个条件,使得$\triangle ABC\cong\triangle ADC$,下列条件添加错误的是(
A.$\angle B= \angle D$
B.$BC = DC$
C.$AB = AD$
D.$\angle 3= \angle 4$
B
)
A.$\angle B= \angle D$
B.$BC = DC$
C.$AB = AD$
D.$\angle 3= \angle 4$
答案:B
解析:
在$\triangle ABC$和$\triangle ADC$中,已知$\angle 1 = \angle 2$,$AC = AC$(公共边)。
若添加条件A:$\angle B = \angle D$,则可由“AAS”判定$\triangle ABC\cong\triangle ADC$;
若添加条件B:$BC = DC$,此时为“SSA”,不能判定$\triangle ABC\cong\triangle ADC$;
若添加条件C:$AB = AD$,则可由“SAS”判定$\triangle ABC\cong\triangle ADC$;
若添加条件D:$\angle 3 = \angle 4$,则可由“ASA”判定$\triangle ABC\cong\triangle ADC$。
B
若添加条件A:$\angle B = \angle D$,则可由“AAS”判定$\triangle ABC\cong\triangle ADC$;
若添加条件B:$BC = DC$,此时为“SSA”,不能判定$\triangle ABC\cong\triangle ADC$;
若添加条件C:$AB = AD$,则可由“SAS”判定$\triangle ABC\cong\triangle ADC$;
若添加条件D:$\angle 3 = \angle 4$,则可由“ASA”判定$\triangle ABC\cong\triangle ADC$。
B
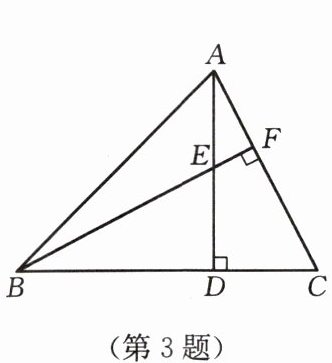
3. 如图,$AD = BD$,$AD\perp BC$,$BF\perp AC$,$BC = 6\ cm$,$DC = 2\ cm$,则$DE= $
2
$cm$。
答案:2
解析:
证明:
∵ $AD \perp BC$,$BF \perp AC$,
∴ $\angle ADB = \angle ADC = \angle BFC = 90°$。
∵ $BC = 6\ cm$,$DC = 2\ cm$,
∴ $BD = BC - DC = 6 - 2 = 4\ cm$。
∵ $AD = BD$,
∴ $AD = 4\ cm$。
∵ $\angle BED = \angle AEF$,$\angle EDB = \angle EFA = 90°$,
∴ $\angle EBD = \angle EAF$。
在$\triangle BDE$和$\triangle ADC$中,
$\begin{cases} \angle EBD = \angle CAD \\BD = AD \\\angle BDE = \angle ADC \end{cases}$,
∴ $\triangle BDE \cong \triangle ADC\ (ASA)$。
∴ $DE = DC = 2\ cm$。
2
∵ $AD \perp BC$,$BF \perp AC$,
∴ $\angle ADB = \angle ADC = \angle BFC = 90°$。
∵ $BC = 6\ cm$,$DC = 2\ cm$,
∴ $BD = BC - DC = 6 - 2 = 4\ cm$。
∵ $AD = BD$,
∴ $AD = 4\ cm$。
∵ $\angle BED = \angle AEF$,$\angle EDB = \angle EFA = 90°$,
∴ $\angle EBD = \angle EAF$。
在$\triangle BDE$和$\triangle ADC$中,
$\begin{cases} \angle EBD = \angle CAD \\BD = AD \\\angle BDE = \angle ADC \end{cases}$,
∴ $\triangle BDE \cong \triangle ADC\ (ASA)$。
∴ $DE = DC = 2\ cm$。
2
4. 如图,已知$\angle B= \angle DEF$,$AB = DE$,要说明$\triangle ABC\cong\triangle DEF$,并且以“ASA”为依据,还需要添加的条件为
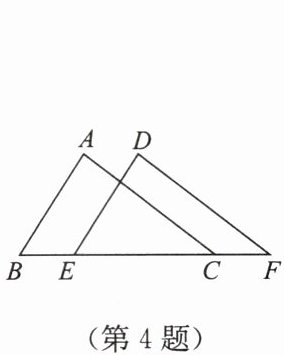
∠A=∠D
。
答案:∠A=∠D
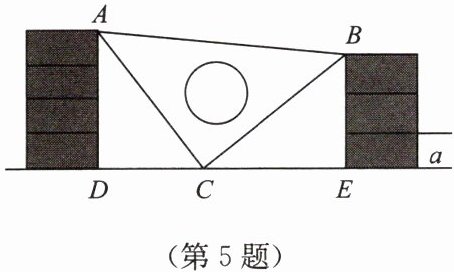
5. 在数学综合实践活动课上,小明将等腰直角三角板放在两堆砖块之间,如图所示。
(1)求证:$\triangle ADC\cong\triangle CEB$;
(2)已知$DE = 35\ cm$,请你帮小明求出每块砖的厚度$a$的大小(每块砖的厚度相同)。
(1)求证:$\triangle ADC\cong\triangle CEB$;
(2)已知$DE = 35\ cm$,请你帮小明求出每块砖的厚度$a$的大小(每块砖的厚度相同)。

答案:(1) 证明:由题意知,三角板为等腰直角三角形,∴AC=BC,∠ACB=90°。
∵砖块竖直放置,∴AD⊥DE,BE⊥DE,∴∠ADC=∠CEB=90°。
∵∠ACB=90°,∴∠ACD+∠BCE=90°。
在Rt△ADC中,∠ACD+∠DAC=90°,∴∠DAC=∠BCE。
在△ADC和△CEB中,
$\left\{\begin{array}{l} ∠ADC=∠CEB\\ ∠DAC=∠ECB\\ AC=CB\end{array}\right.$,
∴△ADC≌△CEB(AAS)。
(2) 设每块砖厚度为a。由(1)知△ADC≌△CEB,∴AD=CE,DC=BE。
设左边砖块有m块,右边有n块,则AD=ma,BE=na,∴CE=ma,DC=na。
∵DE=DC+CE=na+ma=a(m+n),由图可知m+n=7(左右砖块总数),DE=35cm,
∴35=a×7,解得a=5。
(1) 证明完毕;(2) 5cm。
∵砖块竖直放置,∴AD⊥DE,BE⊥DE,∴∠ADC=∠CEB=90°。
∵∠ACB=90°,∴∠ACD+∠BCE=90°。
在Rt△ADC中,∠ACD+∠DAC=90°,∴∠DAC=∠BCE。
在△ADC和△CEB中,
$\left\{\begin{array}{l} ∠ADC=∠CEB\\ ∠DAC=∠ECB\\ AC=CB\end{array}\right.$,
∴△ADC≌△CEB(AAS)。
(2) 设每块砖厚度为a。由(1)知△ADC≌△CEB,∴AD=CE,DC=BE。
设左边砖块有m块,右边有n块,则AD=ma,BE=na,∴CE=ma,DC=na。
∵DE=DC+CE=na+ma=a(m+n),由图可知m+n=7(左右砖块总数),DE=35cm,
∴35=a×7,解得a=5。
(1) 证明完毕;(2) 5cm。
6. 如图,已知在四边形$ABCD$中,点$E在AD$上,$\angle BCE= \angle ACD = 90^{\circ}$,$\angle BAC= \angle D$,$BC = CE$。求证:$AC = CD$。
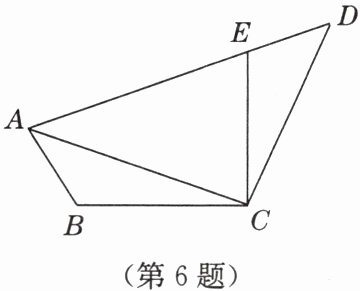

答案:证明:
∵∠BCE=∠ACD=90°,
∴∠BCA=∠ECD.在△BCA和△ECD中,$\left\{\begin{array}{l} ∠BCA=∠ECD,\\ ∠BAC=∠D,\\ BC=CE,\end{array}\right. \therefore \triangle BCA\cong \triangle ECD,\therefore AC=CD.$
∵∠BCE=∠ACD=90°,
∴∠BCA=∠ECD.在△BCA和△ECD中,$\left\{\begin{array}{l} ∠BCA=∠ECD,\\ ∠BAC=∠D,\\ BC=CE,\end{array}\right. \therefore \triangle BCA\cong \triangle ECD,\therefore AC=CD.$