18. (8 分)如图,已知 $ C $ 为射线 $ AD $ 上一点,$ \angle A = \angle B $,$ PA = PB $. 求证:$ CP $ 平分 $ \angle BCD $.
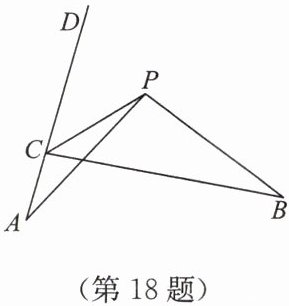

答案:证明:过点P作PE⊥BC于点E, PF⊥AD于点F,则∠BEP=∠AFP=90°. 在△BEP和△AFP中,{∠BEP=∠AFP,∠B=∠A,PB=PA,}
∴△BEP≌△AFP(AAS),
∴PE=PF. 又
∵PE⊥BC, PF⊥AD,
∴CP平分∠BCD.
∴△BEP≌△AFP(AAS),
∴PE=PF. 又
∵PE⊥BC, PF⊥AD,
∴CP平分∠BCD.
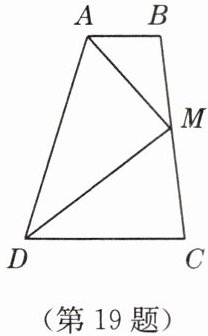
19. (8 分)如图,$ AB // CD $,$ AM $ 平分 $ \angle BAD $,且 $ M $ 是 $ BC $ 的中点.
(1)猜想 $ AD $,$ AB $,$ DC $ 之间的数量关系并证明;
(2)求证:$ DM $ 平分 $ \angle ADC $.
(1)猜想 $ AD $,$ AB $,$ DC $ 之间的数量关系并证明;
(2)求证:$ DM $ 平分 $ \angle ADC $.

答案:
(1) AD=DC+AB. 提示:如图
(1),延长AM, DC相交于点F,先证△ABM≌△FCM,再证AD=DF.
(2) 提示:如图
(2),过点M作MH⊥AB于点H, MI⊥AD于点I, MG⊥CD于点G,先证△BMH≌△CMG,再证△AMH≌△AMI, △DMI≌△DMG.
(1) AD=DC+AB. 提示:如图
(1),延长AM, DC相交于点F,先证△ABM≌△FCM,再证AD=DF.
(2) 提示:如图
(2),过点M作MH⊥AB于点H, MI⊥AD于点I, MG⊥CD于点G,先证△BMH≌△CMG,再证△AMH≌△AMI, △DMI≌△DMG.
20. (8 分)如图,$ AD // BC $,$ \angle A = 90^{\circ} $,以点 $ B $ 为圆心,$ BC $ 长为半径画弧,交射线 $ AD $ 于点 $ E $,连接 $ BE $,过点 $ C $ 作 $ CF \perp BE $,垂足为 $ F $. 求证:$ AB = FC $.
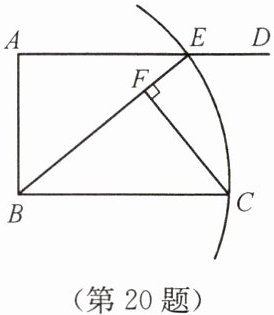

答案:提示:根据AAS证明△ABE≌△FCB.
解析:
证明:
∵ $AD // BC$,
∴ $\angle AEB = \angle FBC$。
∵ $\angle A = 90°$,$CF \perp BE$,
∴ $\angle A = \angle CFB = 90°$。
∵ 以点 $B$ 为圆心,$BC$ 长为半径画弧交 $AD$ 于点 $E$,
∴ $BE = BC$。
在 $\triangle ABE$ 和 $\triangle FCB$ 中,
$\begin{cases} \angle AEB = \angle FBC \\\angle A = \angle CFB \\BE = CB \end{cases}$
∴ $\triangle ABE \cong \triangle FCB\ (AAS)$。
∴ $AB = FC$。
∵ $AD // BC$,
∴ $\angle AEB = \angle FBC$。
∵ $\angle A = 90°$,$CF \perp BE$,
∴ $\angle A = \angle CFB = 90°$。
∵ 以点 $B$ 为圆心,$BC$ 长为半径画弧交 $AD$ 于点 $E$,
∴ $BE = BC$。
在 $\triangle ABE$ 和 $\triangle FCB$ 中,
$\begin{cases} \angle AEB = \angle FBC \\\angle A = \angle CFB \\BE = CB \end{cases}$
∴ $\triangle ABE \cong \triangle FCB\ (AAS)$。
∴ $AB = FC$。
21. (8 分)如图,$ BC = AC $,$ AC \perp BC $,$ AE \perp BE $,$ D $ 是 $ BE $ 与 $ AC $ 的交点,$ BD = 2AE $,$ BE $ 平分 $ \angle ABC $ 吗?请说明理由.
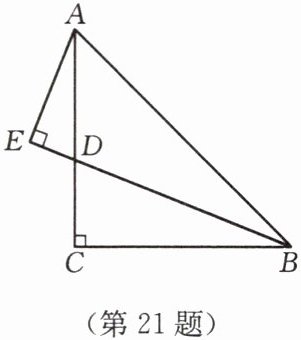

答案:BE平分∠ABC. 提示:延长AE,交BC的延长线于点F,先证△BCD≌△ACF(ASA),再证△ABE≌△FBE(SAS),
∴∠ABE=∠FBE.
∴∠ABE=∠FBE.
22. (12 分)如图,在 $ \triangle ABC $ 中,$ \angle ACB = 90^{\circ} $,$ AC = 6 cm $,$ BC = 8 cm $. 点 $ P $ 从点 $ A $ 出发沿 $ A - C $ 路径向终点 $ C $ 运动;点 $ Q $ 从点 $ B $ 出发沿 $ B - C - A $ 路径向终点 $ A $ 运动. 点 $ P $ 和点 $ Q $ 分别以每秒 $ 1 cm $ 和 $ 3 cm $ 的运动速度同时开始运动,其中一点到达终点时另一点也停止运动,在某时刻,分别过点 $ P $ 和点 $ Q $ 作 $ PE \perp l $ 于点 $ E $,$ QF \perp l $ 于点 $ F $,则点 $ P $ 运动时间为多少秒时,$ \triangle PEC $ 与 $ \triangle QFC $ 全等?
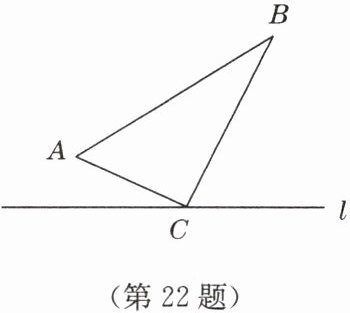

答案:如图
(1),
∵△PEC与△QFC全等,
∴PC=QC.
∴6 - t = 8 - 3t. 解得t = 1. 如图
(2),
∵点P与点Q重合,
∴△PEC与△QFC全等,
∴6 - t = 3t - 8. 解得t=7/2. 综上所述,当点P运动时间为1 s或7/2 s时, △PEC与△QFC全等.
(1),
∵△PEC与△QFC全等,
∴PC=QC.
∴6 - t = 8 - 3t. 解得t = 1. 如图
(2),
∵点P与点Q重合,
∴△PEC与△QFC全等,
∴6 - t = 3t - 8. 解得t=7/2. 综上所述,当点P运动时间为1 s或7/2 s时, △PEC与△QFC全等.