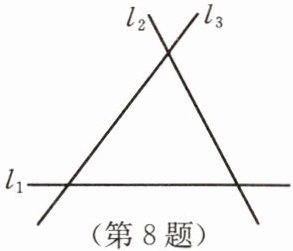
8. 如图,直线 $ l_1 $,$ l_2 $,$ l_3 $ 表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有(
A.1 处
B.2 处
C.3 处
D.4 处
D
)
A.1 处
B.2 处
C.3 处
D.4 处
答案:D
解析:
解:三角形内角平分线的交点到三角形三边的距离相等,三条公路构成三角形,其内角平分线交点有1处;三角形外角平分线的交点到三角形三边所在直线的距离也相等,外角平分线交点有3处。所以共有1+3=4处。
答案:D
答案:D
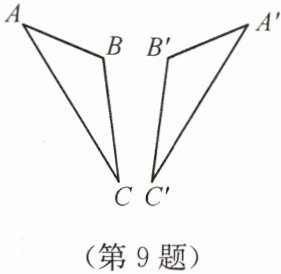
9. 如图,$ \triangle ABC \cong \triangle A'B'C' $,其中 $ \angle A = 36^{\circ} $,$ \angle C' = 24^{\circ} $,则 $ \angle B = $
120°
.
答案:120°
解析:
证明:
∵$\triangle ABC \cong \triangle A'B'C'$,
∴$\angle C = \angle C' = 24°$。
在$\triangle ABC$中,$\angle A + \angle B + \angle C = 180°$,
∵$\angle A = 36°$,$\angle C = 24°$,
∴$\angle B = 180° - \angle A - \angle C = 180° - 36° - 24° = 120°$。
$120°$
∵$\triangle ABC \cong \triangle A'B'C'$,
∴$\angle C = \angle C' = 24°$。
在$\triangle ABC$中,$\angle A + \angle B + \angle C = 180°$,
∵$\angle A = 36°$,$\angle C = 24°$,
∴$\angle B = 180° - \angle A - \angle C = 180° - 36° - 24° = 120°$。
$120°$
10. 如图,$ AD = BC $,$ FD = EC $,再加上条件
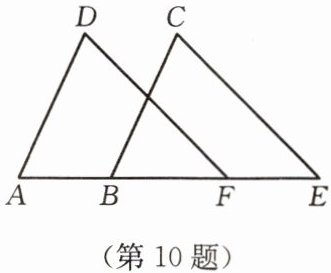
AB=FE(或AF=BE)
,就可证 $ \angle D = \angle C $.
答案:AB=FE(或AF=BE)
11. 如图,$ \angle ACB = \angle BDA = 90^{\circ} $,要利用“HL”证得 $ \triangle ACB \cong \triangle BDA $,还需增加的条件是
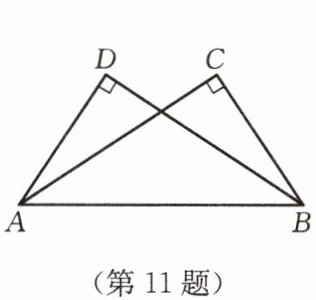
AC=BD(或BC=AD)
.
答案:AC=BD(或BC=AD)
12. 在 $ \triangle ABC $ 中,$ \angle C = 90^{\circ} $,$ AC = BC $,$ AD $ 平分 $ \angle CAB $ 交 $ BC $ 于点 $ D $,$ DE \perp AB $ 于点 $ E $,且 $ AB = 6 cm $,那么 $ \triangle DEB $ 的周长为
6 cm
.答案:6 cm
解析:
∵在$\triangle ABC$中,$\angle C=90^{\circ}$,$AC=BC$,$AB=6\ cm$,
∴$\triangle ABC$是等腰直角三角形,$\angle B=45^{\circ}$。
∵$AD$平分$\angle CAB$,$DE \perp AB$,$\angle C=90^{\circ}$,
∴$CD=DE$(角平分线上的点到角两边的距离相等)。
在$Rt\triangle ACD$和$Rt\triangle AED$中,
$\begin{cases} AD=AD \\ CD=DE \end{cases}$,
∴$Rt\triangle ACD \cong Rt\triangle AED(HL)$,
∴$AC=AE$。
∵$AC=BC$,
∴$AE=BC$。
$\triangle DEB$的周长为$DE+EB+BD$,
∵$CD=DE$,
∴$DE+BD=CD+BD=BC$,
∴$\triangle DEB$的周长为$BC+EB=AE+EB=AB=6\ cm$。
6 cm
13. 如图,在 $ \triangle ABC $ 中,$ AD $ 是 $ \angle BAC $ 的平分线,$ AB : AC = 4 : 3 $,则 $ S_{\triangle ABD} : S_{\triangle ACD} = $
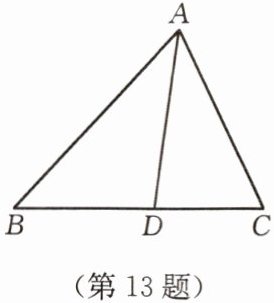
4:3
.
答案:4:3
解析:
证明:过点$D$作$DE \perp AB$于点$E$,$DF \perp AC$于点$F$。
∵$AD$是$\angle BAC$的平分线,
∴$DE = DF$。
∵$S_{\triangle ABD} = \frac{1}{2}AB \cdot DE$,$S_{\triangle ACD} = \frac{1}{2}AC \cdot DF$,
∴$S_{\triangle ABD} : S_{\triangle ACD} = AB : AC$。
∵$AB : AC = 4 : 3$,
∴$S_{\triangle ABD} : S_{\triangle ACD} = 4 : 3$。
4:3
∵$AD$是$\angle BAC$的平分线,
∴$DE = DF$。
∵$S_{\triangle ABD} = \frac{1}{2}AB \cdot DE$,$S_{\triangle ACD} = \frac{1}{2}AC \cdot DF$,
∴$S_{\triangle ABD} : S_{\triangle ACD} = AB : AC$。
∵$AB : AC = 4 : 3$,
∴$S_{\triangle ABD} : S_{\triangle ACD} = 4 : 3$。
4:3
14. 如图,已知 $ AB // CD $,点 $ O $ 为 $ \angle CAB $,$ \angle ACD $ 的平分线的交点,点 $ O $ 到 $ AC $ 的距离为 $ 2 cm $,则两平行线间的距离为
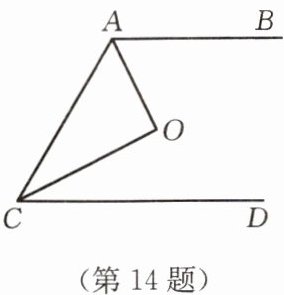
4
$ cm $.
答案:4
解析:
解:过点 $ O $ 作 $ OE \perp AB $ 于点 $ E $,$ OF \perp CD $ 于点 $ F $,$ OG \perp AC $ 于点 $ G $。
因为 $ AO $ 平分 $ \angle CAB $,$ OE \perp AB $,$ OG \perp AC $,所以 $ OE = OG = 2\ cm $。
因为 $ CO $ 平分 $ \angle ACD $,$ OF \perp CD $,$ OG \perp AC $,所以 $ OF = OG = 2\ cm $。
因为 $ AB // CD $,所以 $ E $,$ O $,$ F $ 三点共线,两平行线间的距离为 $ OE + OF = 2 + 2 = 4\ cm $。
4
因为 $ AO $ 平分 $ \angle CAB $,$ OE \perp AB $,$ OG \perp AC $,所以 $ OE = OG = 2\ cm $。
因为 $ CO $ 平分 $ \angle ACD $,$ OF \perp CD $,$ OG \perp AC $,所以 $ OF = OG = 2\ cm $。
因为 $ AB // CD $,所以 $ E $,$ O $,$ F $ 三点共线,两平行线间的距离为 $ OE + OF = 2 + 2 = 4\ cm $。
4
15. 如图,已知在 $ \triangle ABC $ 中,$ AB = AC $,$ AD $ 是角平分线,$ BE = CF $. 有下列说法:(1)$ DA $ 平分 $ \angle EDF $;(2)$ \triangle EBD \cong \triangle FCD $;(3)$ \triangle AED \cong \triangle AFD $. 其中正确的个数是
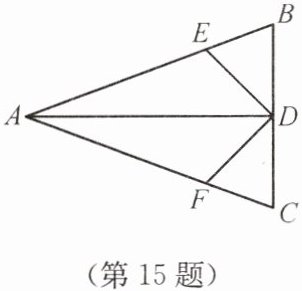
3
.
答案:3
解析:
证明:
∵ $AB=AC$,$AD$是角平分线,
∴ $AD$平分$\angle BAC$,$BD=CD$,$\angle B=\angle C$。
(2)在$\triangle EBD$和$\triangle FCD$中,
$\begin{cases} BE=CF \\ \angle B=\angle C \\ BD=CD \end{cases}$,
∴ $\triangle EBD \cong \triangle FCD$(SAS),故
(2)正确。
由$\triangle EBD \cong \triangle FCD$得$DE=DF$。
(3)在$\triangle AED$和$\triangle AFD$中,
$\begin{cases} AE=AF \\ AD=AD \\ DE=DF \end{cases}$($AE=AB-BE$,$AF=AC-CF$,$AB=AC$,$BE=CF$),
∴ $\triangle AED \cong \triangle AFD$(SSS),故
(3)正确。
由$\triangle AED \cong \triangle AFD$得$\angle EDA=\angle FDA$,
∴ $DA$平分$\angle EDF$,故
(1)正确。
综上,正确的个数是3。
3
∵ $AB=AC$,$AD$是角平分线,
∴ $AD$平分$\angle BAC$,$BD=CD$,$\angle B=\angle C$。
(2)在$\triangle EBD$和$\triangle FCD$中,
$\begin{cases} BE=CF \\ \angle B=\angle C \\ BD=CD \end{cases}$,
∴ $\triangle EBD \cong \triangle FCD$(SAS),故
(2)正确。
由$\triangle EBD \cong \triangle FCD$得$DE=DF$。
(3)在$\triangle AED$和$\triangle AFD$中,
$\begin{cases} AE=AF \\ AD=AD \\ DE=DF \end{cases}$($AE=AB-BE$,$AF=AC-CF$,$AB=AC$,$BE=CF$),
∴ $\triangle AED \cong \triangle AFD$(SSS),故
(3)正确。
由$\triangle AED \cong \triangle AFD$得$\angle EDA=\angle FDA$,
∴ $DA$平分$\angle EDF$,故
(1)正确。
综上,正确的个数是3。
3
16. 如图,在四边形 $ ABCD $ 中,$ \angle A = 90^{\circ} $,$ AD = 3 $,连接 $ BD $,$ BD \perp CD $,$ \angle ADB = \angle C $,若 $ P $ 是 $ BC $ 边上一动点,则 $ DP $ 长的最小值为
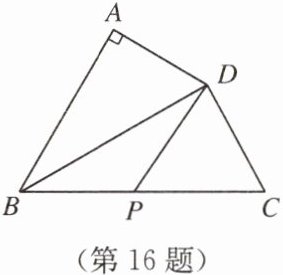
3
.
答案:3
解析:
证明:
∵ $\angle A = 90°$,$BD \perp CD$,
∴ $\angle A = \angle BDC = 90°$。
∵ $\angle ADB = \angle C$,
∴ $\triangle ABD \sim \triangle DBC$(AA相似)。
∴ $\angle ABD = \angle DBC$,即 $BD$ 平分 $\angle ABC$。
∵ $P$ 是 $BC$ 边上一动点,
∴ $DP$ 长的最小值为点 $D$ 到 $BC$ 的距离。
又
∵ 角平分线上的点到角两边距离相等,
∴ 点 $D$ 到 $BC$ 的距离等于 $AD = 3$。
故 $DP$ 长的最小值为 $3$。
答案:$3$
∵ $\angle A = 90°$,$BD \perp CD$,
∴ $\angle A = \angle BDC = 90°$。
∵ $\angle ADB = \angle C$,
∴ $\triangle ABD \sim \triangle DBC$(AA相似)。
∴ $\angle ABD = \angle DBC$,即 $BD$ 平分 $\angle ABC$。
∵ $P$ 是 $BC$ 边上一动点,
∴ $DP$ 长的最小值为点 $D$ 到 $BC$ 的距离。
又
∵ 角平分线上的点到角两边距离相等,
∴ 点 $D$ 到 $BC$ 的距离等于 $AD = 3$。
故 $DP$ 长的最小值为 $3$。
答案:$3$
17. (8 分)如图,点 $ A $,$ F $,$ C $,$ D $ 在同一条直线上,已知 $ AF = DC $,$ \angle A = \angle D $,$ BC // EF $,请写出 $ AB $ 与 $ DE $ 之间的关系并证明你的结论.
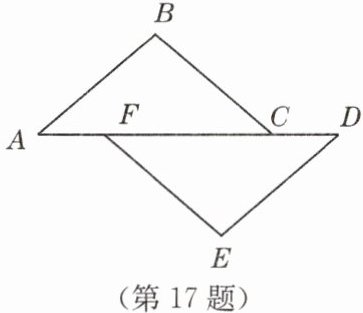

答案:AB//DE, AB=DE, 提示:证△ABC≌△DEF.
解析:
AB与DE的关系是:AB//DE且AB=DE。
证明:
∵AF=DC,
∴AF+FC=DC+FC,即AC=DF。
∵BC//EF,
∴∠ACB=∠DFE。
在△ABC和△DEF中,
$\left\{\begin{array}{l} ∠A=∠D,\\ AC=DF,\\ ∠ACB=∠DFE,\end{array}\right.$
∴△ABC≌△DEF(ASA)。
∴AB=DE,∠B=∠E。
∵∠B=∠E,
∴AB//DE。
综上,AB//DE且AB=DE。
证明:
∵AF=DC,
∴AF+FC=DC+FC,即AC=DF。
∵BC//EF,
∴∠ACB=∠DFE。
在△ABC和△DEF中,
$\left\{\begin{array}{l} ∠A=∠D,\\ AC=DF,\\ ∠ACB=∠DFE,\end{array}\right.$
∴△ABC≌△DEF(ASA)。
∴AB=DE,∠B=∠E。
∵∠B=∠E,
∴AB//DE。
综上,AB//DE且AB=DE。