1. 下列说法中正确的是(
A.两边和其中一边的对角分别相等的两个三角形一定不全等
B.三个角对应相等的两个三角形不一定全等
C.两个面积相等的三角形一定全等
D.有一边相等的两个等腰三角形全等
B
)A.两边和其中一边的对角分别相等的两个三角形一定不全等
B.三个角对应相等的两个三角形不一定全等
C.两个面积相等的三角形一定全等
D.有一边相等的两个等腰三角形全等
答案:B
2. 如图,已知 $ AB = AD $,那么添加下列一个条件后,仍无法判定 $ \triangle ABC \cong \triangle ADC $ 的是(
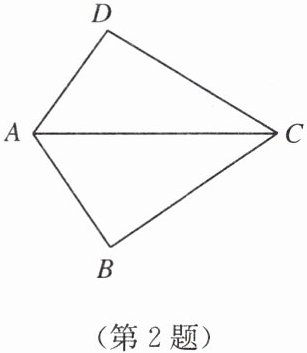
A.$ CB = CD $
B.$ \angle BCA = \angle DCA $
C.$ \angle BAC = \angle DAC $
D.$ \angle B = \angle D = 90^{\circ} $
B
)
A.$ CB = CD $
B.$ \angle BCA = \angle DCA $
C.$ \angle BAC = \angle DAC $
D.$ \angle B = \angle D = 90^{\circ} $
答案:B
解析:
证明:已知 $AB = AD$,$AC = AC$(公共边)。
A. 添加 $CB = CD$,由SSS可判定 $\triangle ABC \cong \triangle ADC$;
B. 添加 $\angle BCA = \angle DCA$,为SSA,无法判定全等;
C. 添加 $\angle BAC = \angle DAC$,由SAS可判定 $\triangle ABC \cong \triangle ADC$;
D. 添加 $\angle B = \angle D = 90°$,由HL可判定 $\triangle ABC \cong \triangle ADC$。
答案:B
A. 添加 $CB = CD$,由SSS可判定 $\triangle ABC \cong \triangle ADC$;
B. 添加 $\angle BCA = \angle DCA$,为SSA,无法判定全等;
C. 添加 $\angle BAC = \angle DAC$,由SAS可判定 $\triangle ABC \cong \triangle ADC$;
D. 添加 $\angle B = \angle D = 90°$,由HL可判定 $\triangle ABC \cong \triangle ADC$。
答案:B
3. 如图,$ AB // CD $,$ BP $ 和 $ CP $ 分别平分 $ \angle ABC $ 和 $ \angle DCB $,$ AD $ 过点 $ P $,且与 $ AB $ 垂直. 若 $ AD = 8 $,则点 $ P $ 到 $ BC $ 的距离是(
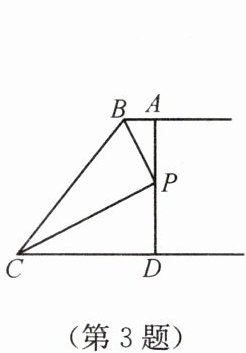
A.8
B.6
C.4
D.2
C
)
A.8
B.6
C.4
D.2
答案:C
解析:
证明:过点 $ P $ 作 $ PE \perp BC $ 于点 $ E $.
∵ $ AB // CD $,$ AD \perp AB $,
∴ $ AD \perp CD $,即 $ PD \perp CD $.
∵ $ BP $ 平分 $ \angle ABC $,$ PA \perp AB $,$ PE \perp BC $,
∴ $ PA = PE $.
∵ $ CP $ 平分 $ \angle DCB $,$ PD \perp CD $,$ PE \perp BC $,
∴ $ PD = PE $.
∴ $ PA = PD = PE $.
∵ $ AD = PA + PD = 8 $,
∴ $ PA = PD = 4 $,
∴ $ PE = 4 $.
答案:C
∵ $ AB // CD $,$ AD \perp AB $,
∴ $ AD \perp CD $,即 $ PD \perp CD $.
∵ $ BP $ 平分 $ \angle ABC $,$ PA \perp AB $,$ PE \perp BC $,
∴ $ PA = PE $.
∵ $ CP $ 平分 $ \angle DCB $,$ PD \perp CD $,$ PE \perp BC $,
∴ $ PD = PE $.
∴ $ PA = PD = PE $.
∵ $ AD = PA + PD = 8 $,
∴ $ PA = PD = 4 $,
∴ $ PE = 4 $.
答案:C
4. 如图,$ AC $,$ BD $ 相交于点 $ O $,且 $ AO = CO $,$ BO = DO $,则图中全等三角形共有(
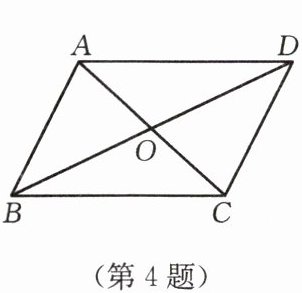
A.2 对
B.3 对
C.4 对
D.5 对
C
)
A.2 对
B.3 对
C.4 对
D.5 对
答案:C
解析:
证明:
∵ $AO=CO$,$BO=DO$,$\angle AOB=\angle COD$,
∴ $\triangle AOB \cong \triangle COD$(SAS);
∵ $AO=CO$,$BO=DO$,$\angle AOD=\angle COB$,
∴ $\triangle AOD \cong \triangle COB$(SAS);
由 $\triangle AOB \cong \triangle COD$ 得 $AB=CD$,
由 $\triangle AOD \cong \triangle COB$ 得 $AD=BC$,
又 $AC=CA$,
∴ $\triangle ABC \cong \triangle CDA$(SSS);
同理,$BD=DB$,
∴ $\triangle ABD \cong \triangle CDB$(SSS)。
综上,全等三角形共4对。
C
∵ $AO=CO$,$BO=DO$,$\angle AOB=\angle COD$,
∴ $\triangle AOB \cong \triangle COD$(SAS);
∵ $AO=CO$,$BO=DO$,$\angle AOD=\angle COB$,
∴ $\triangle AOD \cong \triangle COB$(SAS);
由 $\triangle AOB \cong \triangle COD$ 得 $AB=CD$,
由 $\triangle AOD \cong \triangle COB$ 得 $AD=BC$,
又 $AC=CA$,
∴ $\triangle ABC \cong \triangle CDA$(SSS);
同理,$BD=DB$,
∴ $\triangle ABD \cong \triangle CDB$(SSS)。
综上,全等三角形共4对。
C
5. 如图,已知在 $ \triangle ABC $ 中,$ PR \perp AB $ 于点 $ R $,$ PS \perp AC $ 于点 $ S $,$ PR = PS $,$ \angle 1 = \angle 2 $,则四个结论:① $ AR = AS $;② $ PQ // AB $;③ $ \triangle BPR \cong \triangle CPS $;④ $ BP = CP $ 中(
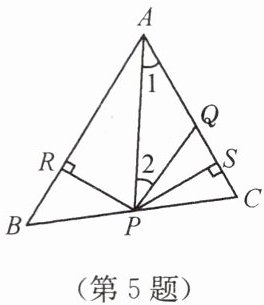
A.全部正确
B.仅①②正确
C.仅①正确
D.仅①④正确
B
)
A.全部正确
B.仅①②正确
C.仅①正确
D.仅①④正确
答案:B
解析:
证明:
1. 在$Rt\triangle APR$和$Rt\triangle APS$中,
$\left\{\begin{array}{l} AP=AP\\ PR=PS\end{array}\right.$
$\therefore Rt\triangle APR\cong Rt\triangle APS(HL)$,
$\therefore AR=AS$,①正确;
2. $\because Rt\triangle APR\cong Rt\triangle APS$,
$\therefore \angle PAR=\angle PAS$,
$\because \angle 1=\angle 2$,
$\therefore \angle PAR+\angle 1=\angle PAS+\angle 2$,即$\angle BAQ=\angle PAQ$,
$\therefore \angle 2=\angle BAQ$,
$\therefore PQ// AB$,②正确;
3. 无法证明$\triangle BPR\cong \triangle CPS$,③错误;
4. 无法证明$BP=CP$,④错误。
结论:仅①②正确,选B。
1. 在$Rt\triangle APR$和$Rt\triangle APS$中,
$\left\{\begin{array}{l} AP=AP\\ PR=PS\end{array}\right.$
$\therefore Rt\triangle APR\cong Rt\triangle APS(HL)$,
$\therefore AR=AS$,①正确;
2. $\because Rt\triangle APR\cong Rt\triangle APS$,
$\therefore \angle PAR=\angle PAS$,
$\because \angle 1=\angle 2$,
$\therefore \angle PAR+\angle 1=\angle PAS+\angle 2$,即$\angle BAQ=\angle PAQ$,
$\therefore \angle 2=\angle BAQ$,
$\therefore PQ// AB$,②正确;
3. 无法证明$\triangle BPR\cong \triangle CPS$,③错误;
4. 无法证明$BP=CP$,④错误。
结论:仅①②正确,选B。
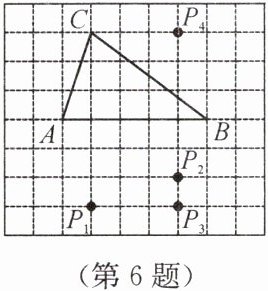
6. 如图,在方格纸中,以 $ AB $ 为一边作 $ \triangle ABP $,使之与 $ \triangle ABC $ 全等,从 $ P_1 $,$ P_2 $,$ P_3 $,$ P_4 $ 四个点中找出符合条件的点 $ P $,则点 $ P $ 有(
A.1 个
B.2 个
C.3 个
D.4 个
C
)
A.1 个
B.2 个
C.3 个
D.4 个
答案:C
解析:
要使$\triangle ABP$与$\triangle ABC$全等,需满足三边对应相等或两边及其夹角对应相等或两角及其夹边对应相等。
已知$AB$为公共边,$\triangle ABC$中,$AC$、$BC$的长度可通过方格计算。
经分析:
点$P_1$:可使$\triangle ABP_1$与$\triangle ABC$全等。
点$P_2$:可使$\triangle ABP_2$与$\triangle ABC$全等。
点$P_3$:可使$\triangle ABP_3$与$\triangle ABC$全等。
点$P_4$:不能使$\triangle ABP_4$与$\triangle ABC$全等。
符合条件的点$P$有$P_1$、$P_2$、$P_3$,共3个。
C
已知$AB$为公共边,$\triangle ABC$中,$AC$、$BC$的长度可通过方格计算。
经分析:
点$P_1$:可使$\triangle ABP_1$与$\triangle ABC$全等。
点$P_2$:可使$\triangle ABP_2$与$\triangle ABC$全等。
点$P_3$:可使$\triangle ABP_3$与$\triangle ABC$全等。
点$P_4$:不能使$\triangle ABP_4$与$\triangle ABC$全等。
符合条件的点$P$有$P_1$、$P_2$、$P_3$,共3个。
C
7. 如果长为 $ l $ 的一根绳子恰好可围成两个全等三角形,那么其中一个三角形的最长边 $ x $ 的取值范围是(
A.$ \frac{l}{6} \leq x < \frac{l}{4} $
B.$ \frac{l}{8} \leq x < \frac{l}{4} $
C.$ \frac{l}{6} < x < \frac{l}{4} $
D.$ \frac{l}{8} < x < \frac{l}{4} $
A
)A.$ \frac{l}{6} \leq x < \frac{l}{4} $
B.$ \frac{l}{8} \leq x < \frac{l}{4} $
C.$ \frac{l}{6} < x < \frac{l}{4} $
D.$ \frac{l}{8} < x < \frac{l}{4} $
答案:A
解析:
两个全等三角形的周长均为$\frac{l}{2}$,设其中一个三角形的三边为$x$,$y$,$z$,且$x \geq y \geq z$。
由周长可得:$x + y + z=\frac{l}{2}$。
根据三角形三边关系,两边之和大于第三边:$y + z > x$,即$\frac{l}{2}-x > x$,解得$x < \frac{l}{4}$。
又因为$x$为最长边,所以$x \geq y$,$x \geq z$,则$y \leq x$,$z \leq x$,故$y + z \leq 2x$,即$\frac{l}{2}-x \leq 2x$,解得$x \geq \frac{l}{6}$。
综上,$\frac{l}{6} \leq x < \frac{l}{4}$。
A
由周长可得:$x + y + z=\frac{l}{2}$。
根据三角形三边关系,两边之和大于第三边:$y + z > x$,即$\frac{l}{2}-x > x$,解得$x < \frac{l}{4}$。
又因为$x$为最长边,所以$x \geq y$,$x \geq z$,则$y \leq x$,$z \leq x$,故$y + z \leq 2x$,即$\frac{l}{2}-x \leq 2x$,解得$x \geq \frac{l}{6}$。
综上,$\frac{l}{6} \leq x < \frac{l}{4}$。
A