7. 如图,在$\triangle ABC$中,$D是BC$边的中点,$DE\perp BC交\angle BAC的平分线于点E$,$EF\perp AB于F$,$EG\perp AC的延长线于G$. 那么$BF = CG$吗?为什么?
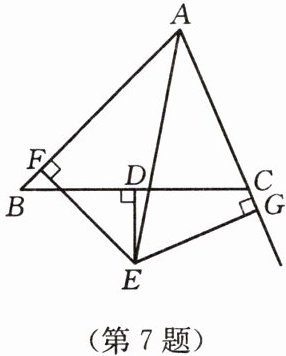

答案:BF=CG. 证明:连接BE,CE.先证△BDE≌△CDE(SAS),
∴EB=EC.
∵AE平分∠BAC,EF⊥AB,EG⊥AC,
∴EF=EG.
再证Rt△BEF≌Rt△CEG(HL),
∴BF=CG.
∴EB=EC.
∵AE平分∠BAC,EF⊥AB,EG⊥AC,
∴EF=EG.
再证Rt△BEF≌Rt△CEG(HL),
∴BF=CG.
8. 如图,在$\triangle ABC$中,$\angle C = 90^{\circ}$,$CA = CB$,点$M在线段AB$上,$\angle GMB= \frac{1}{2}\angle A$,$BG\perp MG$,垂足为$G$,$MG与BC相交于点H$. 若$MH = 8\,cm$,求$BG$的长.
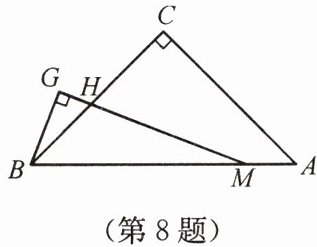

答案:提示:如图,作MD⊥BC于点D,延长MD交BG的延长线于点E,证△BED≌△MHD,得BE=MH,再得BG等于MH的一半,即为4.
解析:
证明:过点$M$作$MD \perp BC$于点$D$,延长$MD$交$BG$的延长线于点$E$。
$\because \angle C=90^{\circ}$,$CA=CB$,$\therefore \angle A=\angle ABC=45^{\circ}$,$\angle GMB=\frac{1}{2}\angle A=22.5^{\circ}$。
$\because BG \perp MG$,$\therefore \angle BGM=90^{\circ}$,$\angle GBM=90^{\circ}-\angle GMB=67.5^{\circ}$,$\angle GBD=\angle GBM-\angle ABC=22.5^{\circ}$。
$\because MD \perp BC$,$\angle ABC=45^{\circ}$,$\therefore \angle BMD=45^{\circ}$,$BD=MD$。
$\because \angle E+\angle GBD=90^{\circ}$,$\angle MHD+\angle GMB=90^{\circ}$,$\angle GBD=\angle GMB=22.5^{\circ}$,$\therefore \angle E=\angle MHD$。
在$\triangle BED$和$\triangle MHD$中,$\left\{\begin{array}{l}\angle E=\angle MHD\\\angle BDE=\angle MDH=90^{\circ}\\BD=MD\end{array}\right.$,$\therefore \triangle BED\cong\triangle MHD(AAS)$,$\therefore BE=MH=8\,cm$。
$\because \angle BMD=45^{\circ}$,$\angle GMB=22.5^{\circ}$,$\therefore \angle GME=22.5^{\circ}=\angle GMB$。
$\because BG \perp MG$,$\therefore \triangle BGE\cong\triangle BGM(ASA)$,$\therefore BG=GE=\frac{1}{2}BE=4\,cm$。
$\therefore BG=4\,cm$。
$\because \angle C=90^{\circ}$,$CA=CB$,$\therefore \angle A=\angle ABC=45^{\circ}$,$\angle GMB=\frac{1}{2}\angle A=22.5^{\circ}$。
$\because BG \perp MG$,$\therefore \angle BGM=90^{\circ}$,$\angle GBM=90^{\circ}-\angle GMB=67.5^{\circ}$,$\angle GBD=\angle GBM-\angle ABC=22.5^{\circ}$。
$\because MD \perp BC$,$\angle ABC=45^{\circ}$,$\therefore \angle BMD=45^{\circ}$,$BD=MD$。
$\because \angle E+\angle GBD=90^{\circ}$,$\angle MHD+\angle GMB=90^{\circ}$,$\angle GBD=\angle GMB=22.5^{\circ}$,$\therefore \angle E=\angle MHD$。
在$\triangle BED$和$\triangle MHD$中,$\left\{\begin{array}{l}\angle E=\angle MHD\\\angle BDE=\angle MDH=90^{\circ}\\BD=MD\end{array}\right.$,$\therefore \triangle BED\cong\triangle MHD(AAS)$,$\therefore BE=MH=8\,cm$。
$\because \angle BMD=45^{\circ}$,$\angle GMB=22.5^{\circ}$,$\therefore \angle GME=22.5^{\circ}=\angle GMB$。
$\because BG \perp MG$,$\therefore \triangle BGE\cong\triangle BGM(ASA)$,$\therefore BG=GE=\frac{1}{2}BE=4\,cm$。
$\therefore BG=4\,cm$。
【观察、猜想、探究】
在$\triangle ABC$中,$\angle ACB = 2\angle B$.
(1)如图(1),当$\angle C = 90^{\circ}$,$AD为\angle BAC$的角平分线时,求证:$AB = AC + CD$.
(2)如图(2),当$\angle C\neq90^{\circ}$,$AD为\angle BAC$的角平分线时,线段$AB$,$AC$,$CD$又有怎样的数量关系?不需要证明,请直接写出你的猜想.
(3)如图(3),当$AD为\triangle ABC$的外角平分线时,线段$AB$,$AC$,$CD$又有怎样的数量关系?请写出你的猜想,并对你的猜想给予证明.
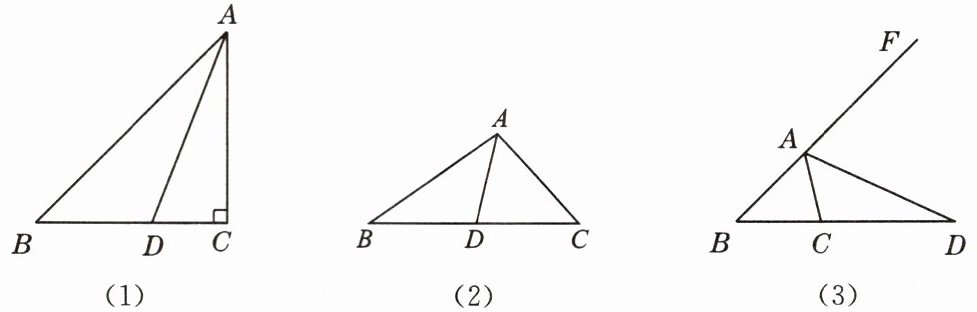
在$\triangle ABC$中,$\angle ACB = 2\angle B$.
(1)如图(1),当$\angle C = 90^{\circ}$,$AD为\angle BAC$的角平分线时,求证:$AB = AC + CD$.
(2)如图(2),当$\angle C\neq90^{\circ}$,$AD为\angle BAC$的角平分线时,线段$AB$,$AC$,$CD$又有怎样的数量关系?不需要证明,请直接写出你的猜想.
(3)如图(3),当$AD为\triangle ABC$的外角平分线时,线段$AB$,$AC$,$CD$又有怎样的数量关系?请写出你的猜想,并对你的猜想给予证明.

答案:(1)提示:过点D作DE⊥AB,交AB于点E.
(2)AB=CD+AC.
(3)AB=CD - AC,提示:在AF上截取AG=AC.
(2)AB=CD+AC.
(3)AB=CD - AC,提示:在AF上截取AG=AC.