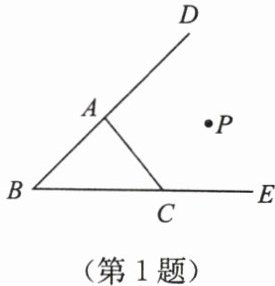
1. 如图,已知点$P到BE$,$BD$,$AC$的距离恰好相等,则点$P$的位置:
(1)在$\angle B$的平分线上;
(2)在$\angle DAC$的平分线上;
(3)在$\angle ECA$的平分线上;
(4)恰是$\angle B$,$\angle DAC$,$\angle ECA$三个角的平分线的交点.
上述结论中,正确结论的个数有(
A. $1$个
B. $2$个
C. $3$个
D. $4$个
(1)在$\angle B$的平分线上;
(2)在$\angle DAC$的平分线上;
(3)在$\angle ECA$的平分线上;
(4)恰是$\angle B$,$\angle DAC$,$\angle ECA$三个角的平分线的交点.
上述结论中,正确结论的个数有(
D
)A. $1$个
B. $2$个
C. $3$个
D. $4$个

答案:D
解析:
证明:
∵点$P$到$BE$、$BD$的距离相等,
∴点$P$在$\angle B$的平分线上,(1)正确;
∵点$P$到$BD$、$AC$的距离相等,
∴点$P$在$\angle DAC$的平分线上,(2)正确;
∵点$P$到$AC$、$BE$的距离相等,
∴点$P$在$\angle ECA$的平分线上,(3)正确;
由(1)(2)(3)知,点$P$是$\angle B$、$\angle DAC$、$\angle ECA$三个角的平分线的交点,(4)正确.
综上,正确结论的个数为$4$个.
D
∵点$P$到$BE$、$BD$的距离相等,
∴点$P$在$\angle B$的平分线上,(1)正确;
∵点$P$到$BD$、$AC$的距离相等,
∴点$P$在$\angle DAC$的平分线上,(2)正确;
∵点$P$到$AC$、$BE$的距离相等,
∴点$P$在$\angle ECA$的平分线上,(3)正确;
由(1)(2)(3)知,点$P$是$\angle B$、$\angle DAC$、$\angle ECA$三个角的平分线的交点,(4)正确.
综上,正确结论的个数为$4$个.
D
2. 在$\triangle ABC$中,$\angle C = 90^{\circ}$,$AC = BC$,$AD是\triangle ABC$的角平分线,$DE\perp AB$,垂足为$E$,若$AB = 10\,cm$,则$\triangle DBE$的周长为(
A.$8\,cm$
B.$9\,cm$
C.$10\,cm$
D.$12\,cm$
C
)A.$8\,cm$
B.$9\,cm$
C.$10\,cm$
D.$12\,cm$
答案:C
解析:
解:
∵在$\triangle ABC$中,$\angle C=90°$,$AC=BC$,
∴$\triangle ABC$为等腰直角三角形,$\angle B=45°$。
∵$AD$是角平分线,$DE\perp AB$,$\angle C=90°$,
∴$DC=DE$(角平分线性质),$AE=AC$(全等三角形对应边相等,$\triangle ACD\cong\triangle AED$)。
设$AC=BC=x$,则$AB=\sqrt{AC^2+BC^2}=\sqrt{2}x=10$,
$\triangle DBE$的周长$=DE+EB+BD=DC+EB+BD=BC+EB=AC+EB=AE+EB=AB=10\,cm$。
C
∵在$\triangle ABC$中,$\angle C=90°$,$AC=BC$,
∴$\triangle ABC$为等腰直角三角形,$\angle B=45°$。
∵$AD$是角平分线,$DE\perp AB$,$\angle C=90°$,
∴$DC=DE$(角平分线性质),$AE=AC$(全等三角形对应边相等,$\triangle ACD\cong\triangle AED$)。
设$AC=BC=x$,则$AB=\sqrt{AC^2+BC^2}=\sqrt{2}x=10$,
$\triangle DBE$的周长$=DE+EB+BD=DC+EB+BD=BC+EB=AC+EB=AE+EB=AB=10\,cm$。
C
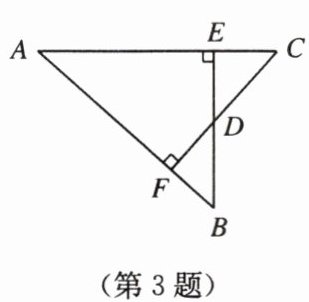
3. 如图,$AB = AC$,$BE\perp AC于点E$,$CF\perp AB于点F$,$BE$,$CF交于点D$. 给出下列结论:①$\triangle ABE\cong\triangle ACF$;②$\triangle BDF\cong\triangle CDE$;③点$D在\angle BAC$的平分线上. 其中,正确的是(
A.①
B.②
C.①②
D.①②③
D
)
A.①
B.②
C.①②
D.①②③
答案:D
解析:
证明:
① $\because BE\perp AC$,$CF\perp AB$,
$\therefore \angle AEB=\angle AFC=90°$,
$\because AB=AC$,$\angle BAE=\angle CAF$,
$\therefore \triangle ABE\cong\triangle ACF(AAS)$,故①正确;
② 由①得 $AE=AF$,$BE=CF$,
$\because AB=AC$,$\therefore BF=AB-AF=AC-AE=CE$,
$\because \angle BFD=\angle CED=90°$,$\angle BDF=\angle CDE$,
$\therefore \triangle BDF\cong\triangle CDE(AAS)$,故②正确;
③ 由②得 $DF=DE$,
$\because BE\perp AC$,$CF\perp AB$,
$\therefore$ 点 $D$ 在 $\angle BAC$ 的平分线上(角平分线性质逆定理),故③正确。
综上,①②③均正确。
答案:D
① $\because BE\perp AC$,$CF\perp AB$,
$\therefore \angle AEB=\angle AFC=90°$,
$\because AB=AC$,$\angle BAE=\angle CAF$,
$\therefore \triangle ABE\cong\triangle ACF(AAS)$,故①正确;
② 由①得 $AE=AF$,$BE=CF$,
$\because AB=AC$,$\therefore BF=AB-AF=AC-AE=CE$,
$\because \angle BFD=\angle CED=90°$,$\angle BDF=\angle CDE$,
$\therefore \triangle BDF\cong\triangle CDE(AAS)$,故②正确;
③ 由②得 $DF=DE$,
$\because BE\perp AC$,$CF\perp AB$,
$\therefore$ 点 $D$ 在 $\angle BAC$ 的平分线上(角平分线性质逆定理),故③正确。
综上,①②③均正确。
答案:D
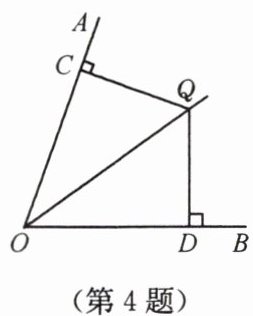
4. 如图,$\angle AOB = 70^{\circ}$,$QC\perp OA于C$,$QD\perp OB于D$,若$QC = QD$,则$\angle AOQ= $
35
$^{\circ}$.
答案:35
解析:
证明:
∵ $QC \perp OA$,$QD \perp OB$,且 $QC = QD$,
∴ 点 $Q$ 在 $\angle AOB$ 的平分线上(角的内部到角两边距离相等的点在角的平分线上)。
∵ $\angle AOB = 70°$,
∴ $\angle AOQ = \frac{1}{2}\angle AOB = \frac{1}{2} × 70° = 35°$。
35
∵ $QC \perp OA$,$QD \perp OB$,且 $QC = QD$,
∴ 点 $Q$ 在 $\angle AOB$ 的平分线上(角的内部到角两边距离相等的点在角的平分线上)。
∵ $\angle AOB = 70°$,
∴ $\angle AOQ = \frac{1}{2}\angle AOB = \frac{1}{2} × 70° = 35°$。
35
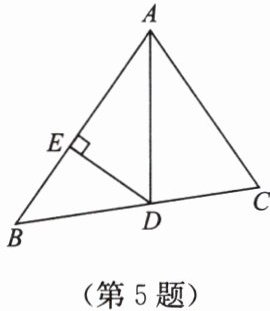
5. 如图,$AD是\triangle ABC中\angle BAC$的平分线,$DE\perp AB于点E$. 若$S_{\triangle ABC} = 7$,$AC = 3$,$AB = 4$,则$DE$的长是
2
.
答案:2
解析:
证明:过点$D$作$DF\perp AC$于点$F$。
因为$AD$是$\angle BAC$的平分线,$DE\perp AB$,$DF\perp AC$,所以$DE = DF$。
设$DE = DF = x$。
$S_{\triangle ABC}=S_{\triangle ABD}+S_{\triangle ACD}$,
$S_{\triangle ABD}=\frac{1}{2}× AB× DE=\frac{1}{2}×4× x = 2x$,
$S_{\triangle ACD}=\frac{1}{2}× AC× DF=\frac{1}{2}×3× x=\frac{3}{2}x$,
所以$2x+\frac{3}{2}x=7$,
解得$x = 2$。
$DE=2$。
答案:$2$
因为$AD$是$\angle BAC$的平分线,$DE\perp AB$,$DF\perp AC$,所以$DE = DF$。
设$DE = DF = x$。
$S_{\triangle ABC}=S_{\triangle ABD}+S_{\triangle ACD}$,
$S_{\triangle ABD}=\frac{1}{2}× AB× DE=\frac{1}{2}×4× x = 2x$,
$S_{\triangle ACD}=\frac{1}{2}× AC× DF=\frac{1}{2}×3× x=\frac{3}{2}x$,
所以$2x+\frac{3}{2}x=7$,
解得$x = 2$。
$DE=2$。
答案:$2$
6. 如图(1),要在$A$区建造一座仓库,使仓库到铁路和公路的距离相等,且离铁路与公路的交叉处$B点700$米,请你在图(2)所示的示意图上画出仓库的位置(保留作图痕迹,不要求写作法).
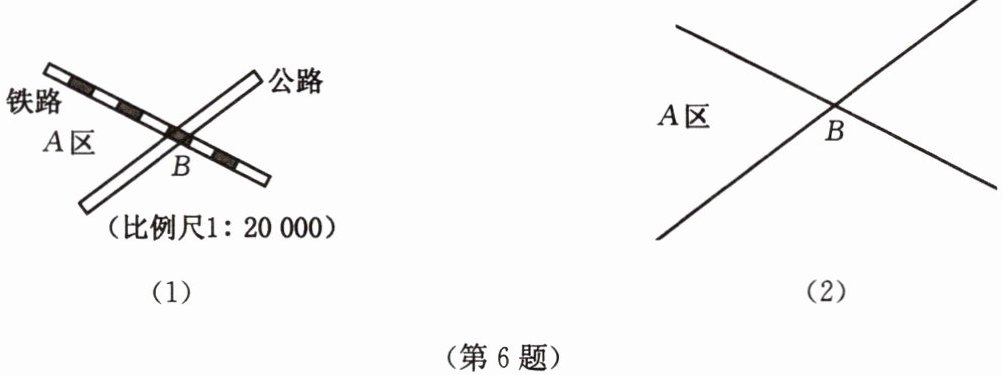

答案:1. 以点B为顶点,作铁路与公路夹角的平分线(尺规作图:以B为圆心画弧交两边于两点,分别以两点为圆心画弧交于一点,过B与交点作射线)。
2. 在该角平分线上,以点B为起点,向A区方向量取3.5厘米(图上距离=700米×100厘米/米×1/20000=3.5厘米),确定仓库位置。
(作图痕迹:角平分线的弧痕、3.5厘米线段的端点标记)
2. 在该角平分线上,以点B为起点,向A区方向量取3.5厘米(图上距离=700米×100厘米/米×1/20000=3.5厘米),确定仓库位置。
(作图痕迹:角平分线的弧痕、3.5厘米线段的端点标记)