如图,$\triangle ABC的外角\angle ACD的平分线CP与内角\angle ABC的平分线BP交于点P$,若$\angle BPC = 40^{\circ}$,求$\angle CAP$的度数.
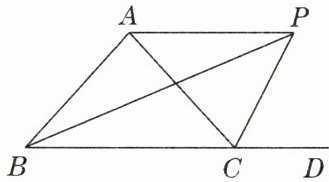

答案:解:延长BA,作PF⊥BA,PN⊥BD,PM⊥AC.设∠PCD=x°,
∵CP平分∠ACD,
∴∠ACP=∠PCD=x°,PM=PN.
∵BP平分∠ABC,
∴∠ABP=∠PBC,PF=PN,
∴PF=PM,
∴AP平分∠CAF,
∴∠CAP=$\frac{1}{2}$∠CAF.
∵∠BPC=40°,
∴∠ABP=∠PBC=∠PCD - ∠BPC=(x - 40)°.
∴∠BAC=∠ACD - ∠ABC=2x°-(x° - 40°)-(x° - 40°)=80°,
∴∠CAF=100°.
∴∠CAP=$\frac{1}{2}$∠CAF=50°.
∵CP平分∠ACD,
∴∠ACP=∠PCD=x°,PM=PN.
∵BP平分∠ABC,
∴∠ABP=∠PBC,PF=PN,
∴PF=PM,
∴AP平分∠CAF,
∴∠CAP=$\frac{1}{2}$∠CAF.
∵∠BPC=40°,
∴∠ABP=∠PBC=∠PCD - ∠BPC=(x - 40)°.
∴∠BAC=∠ACD - ∠ABC=2x°-(x° - 40°)-(x° - 40°)=80°,
∴∠CAF=100°.
∴∠CAP=$\frac{1}{2}$∠CAF=50°.
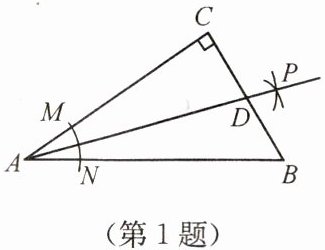
1. 如图,在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,以顶点$A$为圆心,适当长为半径画弧,分别交$AC$,$AB于点M$,$N$,再分别以点$M$,$N$为圆心,大于$\frac{1}{2}MN$的长为半径画弧,两弧交于点$P$,作射线$AP交边BC于点D$,若$CD = 4$,$AB = 15$,则$\triangle ABD$的面积是(
A.$15$
B.$30$
C.$45$
D.$60$
B
)
A.$15$
B.$30$
C.$45$
D.$60$
答案:B
解析:
证明:由作图知,AP是∠CAB的平分线。
过点D作DE⊥AB于点E。
∵∠C=90°,
∴DC⊥AC。
∵AP平分∠CAB,DC⊥AC,DE⊥AB,
∴DE=CD=4。
∴S△ABD=$\frac{1}{2}$×AB×DE=$\frac{1}{2}$×15×4=30。
答案:B
过点D作DE⊥AB于点E。
∵∠C=90°,
∴DC⊥AC。
∵AP平分∠CAB,DC⊥AC,DE⊥AB,
∴DE=CD=4。
∴S△ABD=$\frac{1}{2}$×AB×DE=$\frac{1}{2}$×15×4=30。
答案:B
2. 到三角形三边距离相等的点是三角形三条
角平分线
的交点.答案:角平分线
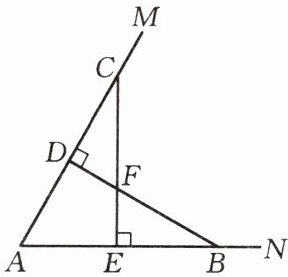
问题 如图,点$B$,$C分别在\angle MAN$的两边上,$BD\perp AM$,$CE\perp AN$,垂足分别为$D$,$E$,$BD$,$CE相交于点F$,且$BF = CF$. 求证:点$F在\angle A$的平分线上.
名师指导
要证明点$F在\angle A$的平分线上,只需证$FE = FD$. 分析已知条件,可以从证明$\triangle BEF\cong\triangle CDF$入手.
解题示范 (学生在教师指导下,独立完成)
证明:
名师指导
要证明点$F在\angle A$的平分线上,只需证$FE = FD$. 分析已知条件,可以从证明$\triangle BEF\cong\triangle CDF$入手.
解题示范 (学生在教师指导下,独立完成)
证明:

答案:证明:
由于$BD \perp AM$且$CE \perp AN$,
根据垂直线的性质,知道$\angle BEF = \angle CDF = 90°$(垂直定义)。
由于$\angle BFE = \angle CFD$(对顶角相等)。
在$\triangle BEF$和$\triangle CDF$中,
$\begin{aligned}\angle BEF = \angle CDF, \\\angle BFE = \angle CFD, \\BF = CF.\end{aligned}$
根据AAS(Angle-Angle-Side)全等条件,得出$\triangle BEF \cong \triangle CDF$。
由于两三角形全等,根据全等三角形的对应边相等,得出$FE = FD$。
$FE \perp AN$且$FD \perp AM$,即$F$到$\angle A$的两边距离相等。
根据角平分线的性质(到角两边距离相等的点在角的平分线上),得出点$F$在$\angle MAN$的平分线上。
由于$BD \perp AM$且$CE \perp AN$,
根据垂直线的性质,知道$\angle BEF = \angle CDF = 90°$(垂直定义)。
由于$\angle BFE = \angle CFD$(对顶角相等)。
在$\triangle BEF$和$\triangle CDF$中,
$\begin{aligned}\angle BEF = \angle CDF, \\\angle BFE = \angle CFD, \\BF = CF.\end{aligned}$
根据AAS(Angle-Angle-Side)全等条件,得出$\triangle BEF \cong \triangle CDF$。
由于两三角形全等,根据全等三角形的对应边相等,得出$FE = FD$。
$FE \perp AN$且$FD \perp AM$,即$F$到$\angle A$的两边距离相等。
根据角平分线的性质(到角两边距离相等的点在角的平分线上),得出点$F$在$\angle MAN$的平分线上。