1. 一个角的平分线的作法,其理论依据是全等三角形判定方法(
A.$AAS$
B.$ASA$
C.$SAS$
D.$SSS$
D
)A.$AAS$
B.$ASA$
C.$SAS$
D.$SSS$
答案:D
2. 点$P在\angle AOB$的平分线上,点$P到OA边的距离等于5$,点$Q是OB$边上的任意一点,则下列选项中正确的是(
A.$PQ\leqslant5$
B.$PQ\lt5$
C.$PQ\geqslant5$
D.$PQ\gt5$
C
)A.$PQ\leqslant5$
B.$PQ\lt5$
C.$PQ\geqslant5$
D.$PQ\gt5$
答案:C
解析:
∵点$P$在$\angle AOB$的平分线上,点$P$到$OA$边的距离等于$5$,
∴点$P$到$OB$边的距离等于$5$。
∵点$Q$是$OB$边上的任意一点,
∴点$P$到$OB$边的距离是点$P$到$OB$边上所有点的最短距离,
∴$PQ\geqslant5$。
C
3. 如图,$AD是\triangle ABC中\angle BAC$的平分线,$DE\perp AB于点E$,$S_{\triangle ABC}= 7$,$DE = 2$,$AB = 4$,则$AC$的长是
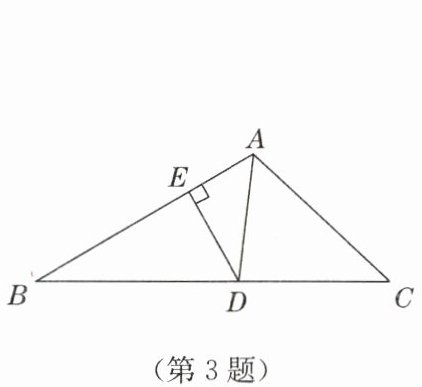
3
.
答案:3
解析:
解:过点D作DF⊥AC于点F。
∵AD是∠BAC的平分线,DE⊥AB,DF⊥AC,
∴DF=DE=2。
∵S△ABC=S△ABD+S△ACD,
S△ABD=$\frac{1}{2}×AB×DE=\frac{1}{2}×4×2=4$,
∴S△ACD=S△ABC-S△ABD=7-4=3。
又
∵S△ACD=$\frac{1}{2}×AC×DF$,
∴$\frac{1}{2}×AC×2=3$,解得AC=3。
3
∵AD是∠BAC的平分线,DE⊥AB,DF⊥AC,
∴DF=DE=2。
∵S△ABC=S△ABD+S△ACD,
S△ABD=$\frac{1}{2}×AB×DE=\frac{1}{2}×4×2=4$,
∴S△ACD=S△ABC-S△ABD=7-4=3。
又
∵S△ACD=$\frac{1}{2}×AC×DF$,
∴$\frac{1}{2}×AC×2=3$,解得AC=3。
3
4. 如图,$OP平分\angle MON$,$PE\perp OM于点E$,$PF\perp ON于点F$,$OA = OB$,则图中有
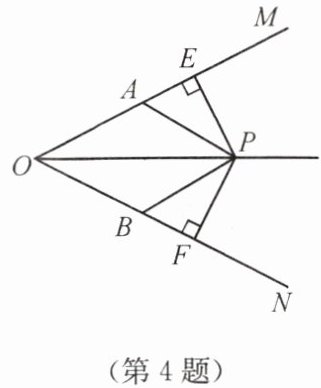
3
对全等三角形.
答案:3
解析:
证明:
∵OP平分∠MON,PE⊥OM,PF⊥ON,
∴PE=PF,∠PEO=∠PFO=90°。
在Rt△POE和Rt△POF中,
$\left\{\begin{array}{l} OP=OP \\ PE=PF \end{array}\right.$,
∴Rt△POE≌Rt△POF(HL)。
在△OPA和△OPB中,
$\left\{\begin{array}{l} OA=OB \\ ∠AOP=∠BOP \\ OP=OP \end{array}\right.$,
∴△OPA≌△OPB(SAS),
∴PA=PB。
在Rt△PEA和Rt△PFB中,
$\left\{\begin{array}{l} PA=PB \\ PE=PF \end{array}\right.$,
∴Rt△PEA≌Rt△PFB(HL)。
综上,全等三角形有3对。
3
∵OP平分∠MON,PE⊥OM,PF⊥ON,
∴PE=PF,∠PEO=∠PFO=90°。
在Rt△POE和Rt△POF中,
$\left\{\begin{array}{l} OP=OP \\ PE=PF \end{array}\right.$,
∴Rt△POE≌Rt△POF(HL)。
在△OPA和△OPB中,
$\left\{\begin{array}{l} OA=OB \\ ∠AOP=∠BOP \\ OP=OP \end{array}\right.$,
∴△OPA≌△OPB(SAS),
∴PA=PB。
在Rt△PEA和Rt△PFB中,
$\left\{\begin{array}{l} PA=PB \\ PE=PF \end{array}\right.$,
∴Rt△PEA≌Rt△PFB(HL)。
综上,全等三角形有3对。
3
5. 如图,$BD是\triangle ABC$的角平分线,$DE\perp AB$,垂足为$E$. 若$\triangle ABC的面积为26$,$AB = 8$,$BC = 5$,则$DE$的长为
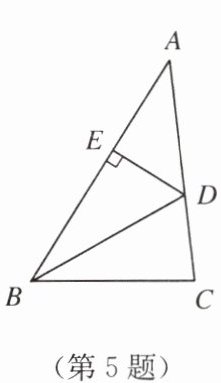
4
.
答案:4
解析:
证明:过点$D$作$DF \perp BC$于点$F$。
因为$BD$是$\triangle ABC$的角平分线,$DE \perp AB$,$DF \perp BC$,所以$DE = DF$。
设$DE = DF = x$。
$\triangle ABC$的面积为$\triangle ABD$与$\triangle CBD$的面积之和,
即$\frac{1}{2} × AB × DE + \frac{1}{2} × BC × DF = 26$。
代入$AB = 8$,$BC = 5$,得$\frac{1}{2} × 8x + \frac{1}{2} × 5x = 26$。
化简得$4x + \frac{5}{2}x = 26$,$\frac{13}{2}x = 26$,解得$x = 4$。
故$DE$的长为$4$。
4
因为$BD$是$\triangle ABC$的角平分线,$DE \perp AB$,$DF \perp BC$,所以$DE = DF$。
设$DE = DF = x$。
$\triangle ABC$的面积为$\triangle ABD$与$\triangle CBD$的面积之和,
即$\frac{1}{2} × AB × DE + \frac{1}{2} × BC × DF = 26$。
代入$AB = 8$,$BC = 5$,得$\frac{1}{2} × 8x + \frac{1}{2} × 5x = 26$。
化简得$4x + \frac{5}{2}x = 26$,$\frac{13}{2}x = 26$,解得$x = 4$。
故$DE$的长为$4$。
4
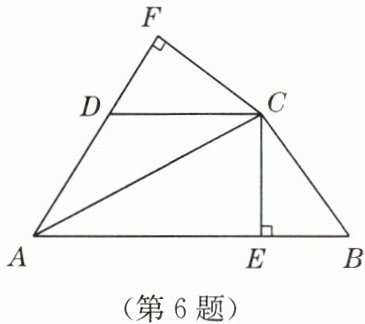
6. 如图,已知$AC平分\angle BAD$,$CE\perp AB于点E$,$CF\perp AD于点F$,且$BC = CD$.
(1)求证:$\triangle BCE\cong\triangle DCF$;
(2)求证:$AB + AD = 2AE$.
(1)求证:$\triangle BCE\cong\triangle DCF$;
(2)求证:$AB + AD = 2AE$.

答案:(1)证明略;(2)提示:证△FAC≌△EAC.
解析:
(1)证明:
∵AC平分∠BAD,CE⊥AB,CF⊥AD,
∴CE=CF,∠CFD=∠CEB=90°.
在Rt△BCE和Rt△DCF中,
$\left\{\begin{array}{l} BC=CD \\ CE=CF\end{array}\right.$,
∴Rt△BCE≌Rt△DCF(HL).
(2)证明:
在Rt△AFC和Rt△AEC中,
$\left\{\begin{array}{l} AC=AC \\ CF=CE\end{array}\right.$,
∴Rt△AFC≌Rt△AEC(HL),
∴AF=AE.
由(1)知Rt△BCE≌Rt△DCF,
∴DF=BE.
∵AD=AF-DF,AB=AE+BE,
∴AB+AD=(AE+BE)+(AF-DF)=AE+AF=2AE.
∵AC平分∠BAD,CE⊥AB,CF⊥AD,
∴CE=CF,∠CFD=∠CEB=90°.
在Rt△BCE和Rt△DCF中,
$\left\{\begin{array}{l} BC=CD \\ CE=CF\end{array}\right.$,
∴Rt△BCE≌Rt△DCF(HL).
(2)证明:
在Rt△AFC和Rt△AEC中,
$\left\{\begin{array}{l} AC=AC \\ CF=CE\end{array}\right.$,
∴Rt△AFC≌Rt△AEC(HL),
∴AF=AE.
由(1)知Rt△BCE≌Rt△DCF,
∴DF=BE.
∵AD=AF-DF,AB=AE+BE,
∴AB+AD=(AE+BE)+(AF-DF)=AE+AF=2AE.
7. 如图,已知$\angle AOB = 90^{\circ}$,$OM是\angle AOB$的平分线,将三角板的直角顶点$P在射线OM$上滑动,两直角边分别与$OA$,$OB交于点C$,$D$,$PC和PD$有怎样的数量关系?请说明理由.
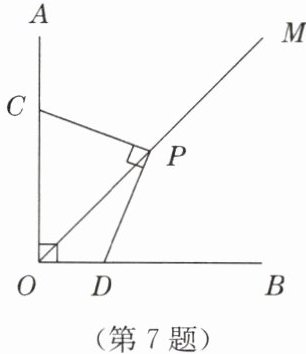

答案:PC=PD. 证明:过点P分别作PE⊥OB于点E,PF⊥OA于点F,
∴∠CFP=∠DEP=90°.
∵∠AOB=90°,
∴∠EPF=90°.
∵OM是∠AOB的平分线,
∴PE=PF.
∵∠AOB=90°,
∴∠FPE=90°,
∴∠2+∠FPD=90°.又∠1+∠FPD=90°,
∴∠1=∠2.
在△CFP和△DEP中,∠CFP=∠DEP,PF=PE,∠1=∠2,
∴△CFP≌△DEP(ASA),
∴PC=PD.
∴∠CFP=∠DEP=90°.
∵∠AOB=90°,
∴∠EPF=90°.
∵OM是∠AOB的平分线,
∴PE=PF.
∵∠AOB=90°,
∴∠FPE=90°,
∴∠2+∠FPD=90°.又∠1+∠FPD=90°,
∴∠1=∠2.
在△CFP和△DEP中,∠CFP=∠DEP,PF=PE,∠1=∠2,
∴△CFP≌△DEP(ASA),
∴PC=PD.