1. 角的平分线上的点到角
两边的距离
相等.答案:两边的距离.
2. 角的内部到角
两边距离
相等的点在角的平分线上.答案:两边距离.
3. 证明命题“角的平分线上的点到角两边的距离相等”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程. 下面是小明同学根据题意画出的图形,并写出了不完整的已知和求证.
已知:如图,$\angle AOP= \angle BOP$,
求证:
请你补全已知和求证,并写出证明过程.
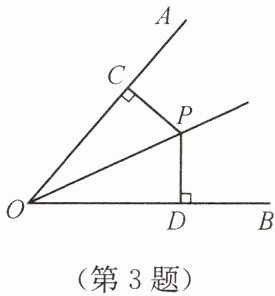
已知:如图,$\angle AOP= \angle BOP$,
PC⊥OA,PD⊥OB,垂足分别为C,D
.求证:
PC=PD
.请你补全已知和求证,并写出证明过程.

答案:PC⊥OA,PD⊥OB,垂足分别为C,D;PC=PD;通过AAS证明△PDO≌△PCO即可.
解析:
已知:如图,$\angle AOP = \angle BOP$,$PC \perp OA$,$PD \perp OB$,垂足分别为$C$,$D$。
求证:$PC = PD$。
证明:因为$PC \perp OA$,$PD \perp OB$,所以$\angle OCP = \angle ODP = 90°$。在$\triangle OCP$和$\triangle ODP$中,$\begin{cases} \angle OCP = \angle ODP \\ \angle AOP = \angle BOP \\ OP = OP \end{cases}$,所以$\triangle OCP \cong \triangle ODP(AAS)$,因此$PC = PD$。
求证:$PC = PD$。
证明:因为$PC \perp OA$,$PD \perp OB$,所以$\angle OCP = \angle ODP = 90°$。在$\triangle OCP$和$\triangle ODP$中,$\begin{cases} \angle OCP = \angle ODP \\ \angle AOP = \angle BOP \\ OP = OP \end{cases}$,所以$\triangle OCP \cong \triangle ODP(AAS)$,因此$PC = PD$。
问题 如图,点$B$,$C在\angle A$的两边上,且$AB = AC$,$D为\angle A$内一点,$DB = DC$,$DE\perp AB$,$DF\perp AC$,垂足分别为$E$,$F$. 求证:$DE = DF$.
名师指导
由已知条件很容易想到连接$AD$,证明$\triangle ACD\cong\triangle ABD$,从而有$\angle BAD= \angle CAD$,于是$D是\angle BAC$平分线上一点,可以用角平分线的性质证得$DE = DF$.
解题示范 (学生在教师指导下,独立完成)
证明:
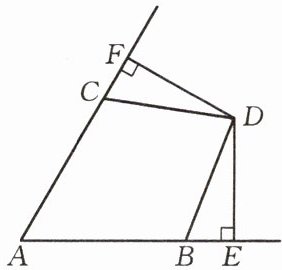
名师指导
由已知条件很容易想到连接$AD$,证明$\triangle ACD\cong\triangle ABD$,从而有$\angle BAD= \angle CAD$,于是$D是\angle BAC$平分线上一点,可以用角平分线的性质证得$DE = DF$.
解题示范 (学生在教师指导下,独立完成)
证明:

答案:证明:
连接 $AD$。
在 $\triangle ABD$ 和 $\triangle ACD$ 中:
$AB = AC$,
$DB = DC$,
$AD = AD$(公共边)。
由 $SSS$ 三角形的全等判定,$\triangle ABD \cong \triangle ACD$。
因此,$\angle BAD = \angle CAD$,即 $AD$ 是 $\angle BAC$ 的平分线。
由于 $DE \perp AB$,$DF \perp AC$,且 $AD$ 是 $\angle BAC$ 的平分线,根据角平分线的性质,$DE = DF$。
所以,$DE = DF$ 得证。
连接 $AD$。
在 $\triangle ABD$ 和 $\triangle ACD$ 中:
$AB = AC$,
$DB = DC$,
$AD = AD$(公共边)。
由 $SSS$ 三角形的全等判定,$\triangle ABD \cong \triangle ACD$。
因此,$\angle BAD = \angle CAD$,即 $AD$ 是 $\angle BAC$ 的平分线。
由于 $DE \perp AB$,$DF \perp AC$,且 $AD$ 是 $\angle BAC$ 的平分线,根据角平分线的性质,$DE = DF$。
所以,$DE = DF$ 得证。