【问题提出】
学习了三角形全等的判定方法(即“SAS”“ASA”“AAS”“SSS”)和直角三角形全等的判定方法(即“HL”)后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究。
【初步思考】
我们不妨将问题用符号语言表示为:在$\triangle ABC和\triangle DEF$中,$AC = DF$,$BC = EF$,$\angle B= \angle E$,然后对$\angle B$进行分类讨论,可以分为“$\angle B$是直角、钝角、锐角”三种情况进行探究。
【深入探究】
第一种情况:当$\angle B$为直角时,$\triangle ABC\cong\triangle DEF$。
(1)如图(1),在$\triangle ABC和\triangle DEF$中,$AC = DF$,$BC = EF$,$\angle B= \angle E = 90^{\circ}$,根据
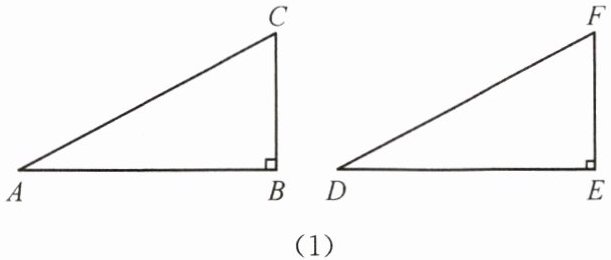
第二种情况:当$\angle B$为钝角时,$\triangle ABC\cong\triangle DEF$。
(2)如图(2),在$\triangle ABC和\triangle DEF$中,$AC = DF$,$BC = EF$,$\angle B= \angle E$,且$\angle B$,$\angle E$都是钝角,求证:$\triangle ABC\cong\triangle DEF$。
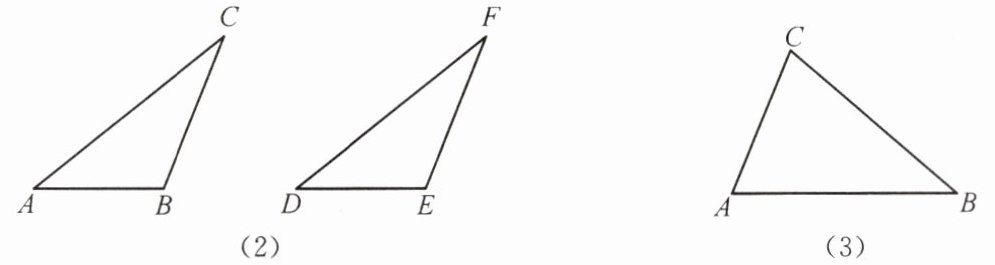
第三种情况:当$\angle B$为锐角时,$\triangle ABC和\triangle DEF$不一定全等。
(3)在$\triangle ABC和\triangle DEF$中,$AC = DF$,$BC = EF$,$\angle B= \angle E$,且$\angle B$,$\angle E$都是锐角,请你用尺规在图(3)中作出$\triangle DEF$,使$\triangle DEF和\triangle ABC$不全等。(不写作法,保留作图痕迹)
(4)$\angle B$还要满足什么条件,就可以使得$\triangle ABC\cong\triangle DEF$,请直接填写结论:
在$\triangle ABC和\triangle DEF$中,$AC = DF$,$BC = EF$,$\angle B= \angle E$,且$\angle B$,$\angle E$都是锐角,若
(2) 证明:分别过点C、F作CM⊥AB交AB延长线于M,FN⊥DE交DE延长线于N。
∵∠B、∠E为钝角,∴∠CBM=180°-∠B,∠FEN=180°-∠E,又∠B=∠E,∴∠CBM=∠FEN。
在△CBM和△FEN中,∠CMB=∠FNE=90°,∠CBM=∠FEN,BC=EF,∴△CBM≌△FEN(AAS),∴CM=FN,BM=EN。
在Rt△ACM和Rt△DFN中,AC=DF,CM=FN,∴Rt△ACM≌Rt△DFN(HL),∴AM=DN。
∵AM=AB+BM,DN=DE+EN,BM=EN,∴AB=DE。
在△ABC和△DEF中,AB=DE,∠B=∠E,BC=EF,∴△ABC≌△DEF(SAS)。
学习了三角形全等的判定方法(即“SAS”“ASA”“AAS”“SSS”)和直角三角形全等的判定方法(即“HL”)后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究。
【初步思考】
我们不妨将问题用符号语言表示为:在$\triangle ABC和\triangle DEF$中,$AC = DF$,$BC = EF$,$\angle B= \angle E$,然后对$\angle B$进行分类讨论,可以分为“$\angle B$是直角、钝角、锐角”三种情况进行探究。
【深入探究】
第一种情况:当$\angle B$为直角时,$\triangle ABC\cong\triangle DEF$。
(1)如图(1),在$\triangle ABC和\triangle DEF$中,$AC = DF$,$BC = EF$,$\angle B= \angle E = 90^{\circ}$,根据
HL
,可以知道$Rt\triangle ABC\cong Rt\triangle DEF$。
第二种情况:当$\angle B$为钝角时,$\triangle ABC\cong\triangle DEF$。
(2)如图(2),在$\triangle ABC和\triangle DEF$中,$AC = DF$,$BC = EF$,$\angle B= \angle E$,且$\angle B$,$\angle E$都是钝角,求证:$\triangle ABC\cong\triangle DEF$。

第三种情况:当$\angle B$为锐角时,$\triangle ABC和\triangle DEF$不一定全等。
(3)在$\triangle ABC和\triangle DEF$中,$AC = DF$,$BC = EF$,$\angle B= \angle E$,且$\angle B$,$\angle E$都是锐角,请你用尺规在图(3)中作出$\triangle DEF$,使$\triangle DEF和\triangle ABC$不全等。(不写作法,保留作图痕迹)
(4)$\angle B$还要满足什么条件,就可以使得$\triangle ABC\cong\triangle DEF$,请直接填写结论:
在$\triangle ABC和\triangle DEF$中,$AC = DF$,$BC = EF$,$\angle B= \angle E$,且$\angle B$,$\angle E$都是锐角,若
AC≥BC
,则$\triangle ABC\cong\triangle DEF$。(2) 证明:分别过点C、F作CM⊥AB交AB延长线于M,FN⊥DE交DE延长线于N。
∵∠B、∠E为钝角,∴∠CBM=180°-∠B,∠FEN=180°-∠E,又∠B=∠E,∴∠CBM=∠FEN。
在△CBM和△FEN中,∠CMB=∠FNE=90°,∠CBM=∠FEN,BC=EF,∴△CBM≌△FEN(AAS),∴CM=FN,BM=EN。
在Rt△ACM和Rt△DFN中,AC=DF,CM=FN,∴Rt△ACM≌Rt△DFN(HL),∴AM=DN。
∵AM=AB+BM,DN=DE+EN,BM=EN,∴AB=DE。
在△ABC和△DEF中,AB=DE,∠B=∠E,BC=EF,∴△ABC≌△DEF(SAS)。
(3) 作图略(以E为顶点作∠E=∠B,在一边截取EF=BC,以F为圆心AC长为半径画弧,与另一边交于异于原位置的点D,连接FD、ED即可)。
答案:(1) HL
(2) 证明:分别过点C、F作CM⊥AB交AB延长线于M,FN⊥DE交DE延长线于N。
∵∠B、∠E为钝角,∴∠CBM=180°-∠B,∠FEN=180°-∠E,又∠B=∠E,∴∠CBM=∠FEN。
在△CBM和△FEN中,∠CMB=∠FNE=90°,∠CBM=∠FEN,BC=EF,∴△CBM≌△FEN(AAS),∴CM=FN,BM=EN。
在Rt△ACM和Rt△DFN中,AC=DF,CM=FN,∴Rt△ACM≌Rt△DFN(HL),∴AM=DN。
∵AM=AB+BM,DN=DE+EN,BM=EN,∴AB=DE。
在△ABC和△DEF中,AB=DE,∠B=∠E,BC=EF,∴△ABC≌△DEF(SAS)。
(3) 作图略(以E为顶点作∠E=∠B,在一边截取EF=BC,以F为圆心AC长为半径画弧,与另一边交于异于原位置的点D,连接FD、ED即可)。
(4) AC≥BC
(2) 证明:分别过点C、F作CM⊥AB交AB延长线于M,FN⊥DE交DE延长线于N。
∵∠B、∠E为钝角,∴∠CBM=180°-∠B,∠FEN=180°-∠E,又∠B=∠E,∴∠CBM=∠FEN。
在△CBM和△FEN中,∠CMB=∠FNE=90°,∠CBM=∠FEN,BC=EF,∴△CBM≌△FEN(AAS),∴CM=FN,BM=EN。
在Rt△ACM和Rt△DFN中,AC=DF,CM=FN,∴Rt△ACM≌Rt△DFN(HL),∴AM=DN。
∵AM=AB+BM,DN=DE+EN,BM=EN,∴AB=DE。
在△ABC和△DEF中,AB=DE,∠B=∠E,BC=EF,∴△ABC≌△DEF(SAS)。
(3) 作图略(以E为顶点作∠E=∠B,在一边截取EF=BC,以F为圆心AC长为半径画弧,与另一边交于异于原位置的点D,连接FD、ED即可)。
(4) AC≥BC