2025年新课程自主学习与测评八年级数学上册人教版第29页解析答案

3. 已知线段$a$,$h$($a＞h$),画$\triangle ABC$,使$AB = AC = a$,$BC边上的高AD = h$。

答案：画法:
(1)画直线MN;
(2)画直线MN的垂线PQ,垂足为D;
(3)在射线DP上截取DA=h;
(4)以A为圆心,a为半径画弧,分别交直线MN于B,C;
(5)连接AB,AC.△ABC为所求作的三角形. 图形略.

4. 如图,$BE\perp CD$,$BE = DE$,$BC = DA$。求证：
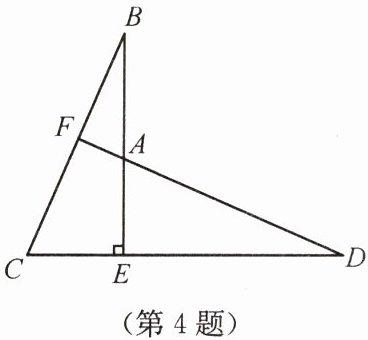
(1)$\triangle BEC\cong\triangle DEA$；
(2)$DF\perp BC$。

答案：
(1)利用HL证△BEC≌△DEA;
(2)∠D + ∠C=90°.

5. 如图,在$\triangle ABC$中,$AC = BC$,直线$l经过顶点C$,过$A$,$B两点分别作l的垂线AE$,$BF$,$E$,$F$为垂足,$AE = CF$。求证：$\angle ACB = 90^{\circ}$。

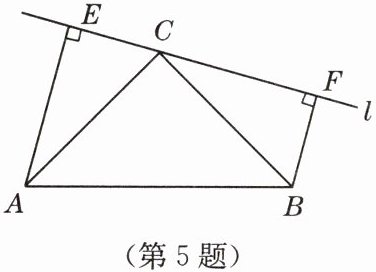
答案：证明:在Rt△ACE和Rt△CBF中,$\left\{\begin{array}{l} AC=BC,\\ AE=CF,\end{array}\right. \therefore Rt\triangle ACE\cong Rt\triangle CBF(HL),\therefore ∠EAC=∠BCF.\because ∠EAC + ∠ACE=90°,\therefore ∠ACE + ∠BCF=90°,\therefore ∠ACB=180° - 90°=90°.$

解析：

证明：
∵AE⊥l，BF⊥l，
∴∠AEC=∠CFB=90°。
在Rt△ACE和Rt△CBF中，
$\left\{\begin{array}{l} AC=BC,\\ AE=CF,\end{array}\right.$
∴Rt△ACE≌Rt△CBF(HL)，
∴∠EAC=∠BCF。
∵∠EAC+∠ACE=90°，
∴∠ACE+∠BCF=90°，
∴∠ACB=180°-90°=90°。

6. 如图,已知点$E$,$F在线段BD$上,$AF\perp BD$,$CE\perp BD$,$AD = CB$,$DE = BF$。求证：$AF = CE$。

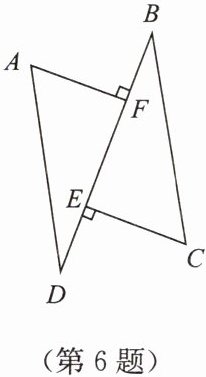
答案：证明:
∵DE=BF,
∴DE + EF=BF + EF,
∴DF=BE.在Rt△ADF和Rt△CBE中,$\left\{\begin{array}{l} AD=CB,\\ DF=BE,\end{array}\right. \therefore Rt\triangle ADF\cong Rt\triangle CBE(HL),\therefore AF=CE.$

7. 如图,在$\triangle ABC$中,$\angle ACB = 90^{\circ}$,$CA = CB$,点$F为BC$延长线上一点,点$E在AC$上,且$AF = BE$。
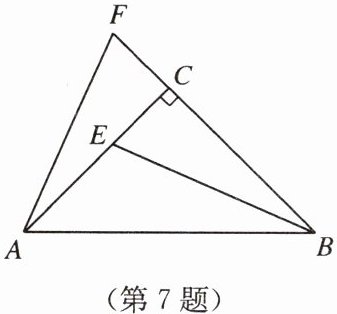
(1)求证：$\triangle ACF\cong\triangle BCE$；
(2)若$\angle ABE = 23^{\circ}$,求$\angle BAF$的度数。

答案：
(1)
∵∠ACB=90°,
∴∠ACF=90°.在Rt△ACF和Rt△BCE中,$\left\{\begin{array}{l} AF=BE,\\ AC=CB,\end{array}\right. \therefore Rt\triangle ACF\cong Rt\triangle BCE(HL).(2)∵∠ACB=90°,CA=CB,∴∠ABC=∠BAC=45°.∵∠ABE=23°,∴∠CBE=∠ABC - ∠ABE=45° - 23°=22°.∵Rt△ACF≌Rt△BCE,∴∠CAF=∠CBE=22°,∴∠BAF=∠CAF + ∠BAC=22° + 45°=67°.$