1. 斜边和一直角边
分别相等
的两个直角
三角形全等(可以简写成“斜边、直角边
”或“HL
”)。答案:分别相等;直角;斜边、直角边;HL
2. 如图,$\angle ACB= \angle BDA = 90^{\circ}$,利用“HL”证明$\triangle ACB\cong\triangle BDA$,你添加的条件是
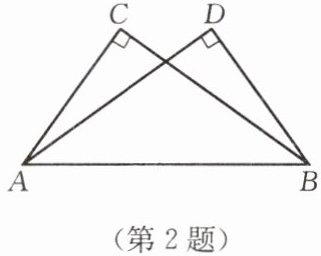
AC=BD或BC=AD
。(不添加字母和辅助线)
答案:AC=BD或BC=AD
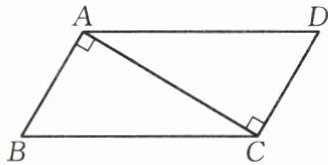
问题 如图,$AB\perp AC$,$CD\perp AC$,$AD = BC$。
求证:$AD// BC$。
名师指导
两个直角三角形的斜边和一直角边分别相等,可利用“HL”证明它们全等,从而得到$\angle ACB= \angle CAD$。
解题示范(学生在教师指导下,独立完成)
证明:
求证:$AD// BC$。
名师指导
两个直角三角形的斜边和一直角边分别相等,可利用“HL”证明它们全等,从而得到$\angle ACB= \angle CAD$。
解题示范(学生在教师指导下,独立完成)
证明:

答案:证明:
因为$AB\perp AC$,$CD\perp AC$,
所以$\angle BAC = \angle DCA = 90^{\circ}$。
在$Rt\triangle ABC$和$Rt\triangle CAD$中,
$AD = BC$,$AC = CA$(公共边)。
根据“$HL$”定理,$Rt\triangle ABC\cong Rt\triangle CAD$。
所以$\angle ACB=\angle CAD$。
因为内错角相等,两直线平行,
所以$AD// BC$。
因为$AB\perp AC$,$CD\perp AC$,
所以$\angle BAC = \angle DCA = 90^{\circ}$。
在$Rt\triangle ABC$和$Rt\triangle CAD$中,
$AD = BC$,$AC = CA$(公共边)。
根据“$HL$”定理,$Rt\triangle ABC\cong Rt\triangle CAD$。
所以$\angle ACB=\angle CAD$。
因为内错角相等,两直线平行,
所以$AD// BC$。
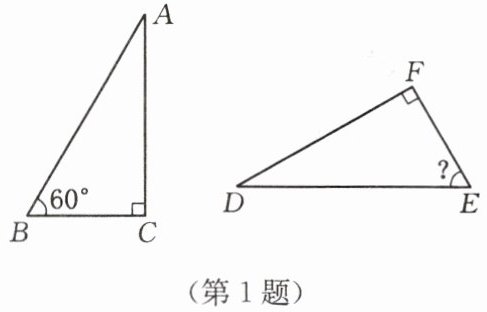
1. 如图,已知$Rt\triangle ABC\cong Rt\triangle DEF$,则$\angle E$的度数为(
A.$30^{\circ}$
B.$45^{\circ}$
C.$60^{\circ}$
D.$90^{\circ}$
C
)
A.$30^{\circ}$
B.$45^{\circ}$
C.$60^{\circ}$
D.$90^{\circ}$
答案:C
解析:
在$Rt\triangle ABC$中,$\angle C=90^{\circ}$,$\angle B=60^{\circ}$,则$\angle A=180^{\circ}-\angle B-\angle C=180^{\circ}-60^{\circ}-90^{\circ}=30^{\circ}$。
因为$Rt\triangle ABC\cong Rt\triangle DEF$,所以对应角相等。由图可知,$\angle E$与$\angle B$是对应角,故$\angle E=\angle B=60^{\circ}$。
答案:C
因为$Rt\triangle ABC\cong Rt\triangle DEF$,所以对应角相等。由图可知,$\angle E$与$\angle B$是对应角,故$\angle E=\angle B=60^{\circ}$。
答案:C
2. 如图,$AC\perp BC于点C$,$BD\perp AD于点D$,要根据“HL”直接证明$Rt\triangle ABC与Rt\triangle BAD$全等,则还需要添加一个条件是(
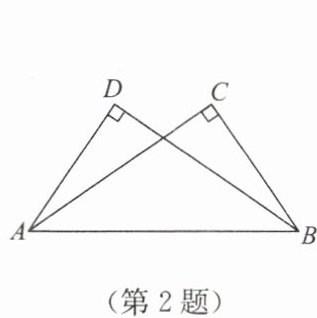
A.$\angle CAB= \angle DBA$
B.$AB = BD$
C.$\angle ABC= \angle BAD$
D.$BC = AD$
D
)
A.$\angle CAB= \angle DBA$
B.$AB = BD$
C.$\angle ABC= \angle BAD$
D.$BC = AD$
答案:D
解析:
证明:
∵ $AC \perp BC$,$BD \perp AD$,
∴ $\triangle ABC$ 和 $\triangle BAD$ 均为直角三角形,且公共斜边 $AB = BA$。
根据“HL”判定定理,需添加一组直角边对应相等。
选项中只有 $BC = AD$ 为直角边对应相等条件。
D
∵ $AC \perp BC$,$BD \perp AD$,
∴ $\triangle ABC$ 和 $\triangle BAD$ 均为直角三角形,且公共斜边 $AB = BA$。
根据“HL”判定定理,需添加一组直角边对应相等。
选项中只有 $BC = AD$ 为直角边对应相等条件。
D