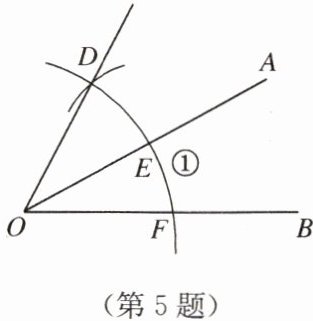
5. 如图,已知$\angle AOB$,以点$O$为圆心,以任意长为半径画弧①,分别交$OA$,$OB于点E$,$F$,再以点$E$为圆心,以$EF$长为半径画弧,交弧①于点$D$,画射线$OD$。若$\angle AOB = 28^{\circ}$,则$\angle BOD$的补角的度数为(
A.$124^{\circ}$
B.$39^{\circ}$
C.$56^{\circ}$
D.$144^{\circ}$
A
)
A.$124^{\circ}$
B.$39^{\circ}$
C.$56^{\circ}$
D.$144^{\circ}$
答案:A
解析:
解:由作图可知,OE=OF=OD,EF=ED。
在△OEF和△OED中,OE=OE,OF=OD,EF=ED,
∴△OEF≌△OED(SSS),
∴∠AOB=∠AOD=28°,
∴∠BOD=∠AOB+∠AOD=28°+28°=56°,
∴∠BOD的补角=180°-56°=124°。
答案:A
在△OEF和△OED中,OE=OE,OF=OD,EF=ED,
∴△OEF≌△OED(SSS),
∴∠AOB=∠AOD=28°,
∴∠BOD=∠AOB+∠AOD=28°+28°=56°,
∴∠BOD的补角=180°-56°=124°。
答案:A
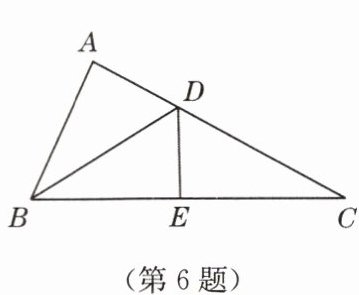
6. 如图,在$\triangle ABC$中,$AD = DE$,$AB = BE$,$\angle A = 85^{\circ}$,则$\angle DEC= $
95
$^{\circ}$。
答案:95
解析:
证明:在$\triangle ABD$和$\triangle EBD$中,
$\begin{cases}AD = DE \\AB = BE \\BD = BD\end{cases}$
$\therefore \triangle ABD \cong \triangle EBD$(SSS)
$\therefore \angle A = \angle BED = 85°$
$\because \angle BED + \angle DEC = 180°$
$\therefore \angle DEC = 180° - 85° = 95°$
$95$
$\begin{cases}AD = DE \\AB = BE \\BD = BD\end{cases}$
$\therefore \triangle ABD \cong \triangle EBD$(SSS)
$\therefore \angle A = \angle BED = 85°$
$\because \angle BED + \angle DEC = 180°$
$\therefore \angle DEC = 180° - 85° = 95°$
$95$
7. 如图,已知$BC = DE$,$AB = AD$,$AC = AE$。求证:$\angle BAD= \angle CAE$。
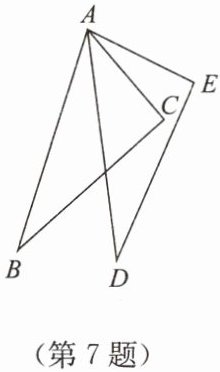

答案:证明:在△ABC和△ADE中,$\left\{\begin{array}{l} AB=AD,\\ BC=DE,\\ AC=AE,\end{array}\right. \therefore \triangle ABC\cong \triangle ADE(SSS).\therefore ∠BAC=∠DAE,\therefore ∠BAC - ∠DAC=∠DAE - ∠DAC,即∠BAD=∠CAE.$
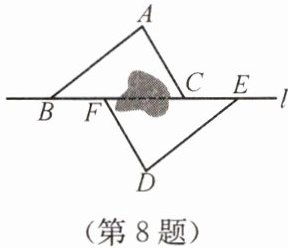
8. 如图,点$B$,$F$,$C$,$E在直线l$上($F$,$C$之间不能直接测量),点$A$,$D在l$异侧,测得$AB = DE$,$AC = DF$,$BF = EC$。
(1)求证:$\triangle ABC\cong\triangle DEF$;
(2)指出图中所有平行的线段,并说明理由。
(1)求证:$\triangle ABC\cong\triangle DEF$;
(2)指出图中所有平行的线段,并说明理由。

答案:
(1)根据SSS证明;
(2)AB//DE,AC//DF,理由略.
(1)根据SSS证明;
(2)AB//DE,AC//DF,理由略.
小明在做数学作业时,遇到这样一道题:如图,$AB = CD$,$CB = AD$,请说明$\angle A= \angle C$的理由。小明动手测量了一下,发现$\angle A确实等于\angle C$,但他不能说明其中的理由,你能帮助他吗?

答案:理由:连接BD.在△ABD和△CDB中,$\left\{\begin{array}{l} AB=CD,\\ AD=CB,\\ BD=DB,\end{array}\right. \therefore \triangle ABD\cong \triangle CDB.\therefore ∠A=∠C.$
解析:
证明:连接$BD$。
在$\triangle ABD$和$\triangle CDB$中,
$\begin{cases}AB = CD, \\AD = CB, \\BD = DB,\end{cases}$
$\therefore \triangle ABD \cong \triangle CDB$(SSS)。
$\therefore \angle A = \angle C$。
在$\triangle ABD$和$\triangle CDB$中,
$\begin{cases}AB = CD, \\AD = CB, \\BD = DB,\end{cases}$
$\therefore \triangle ABD \cong \triangle CDB$(SSS)。
$\therefore \angle A = \angle C$。