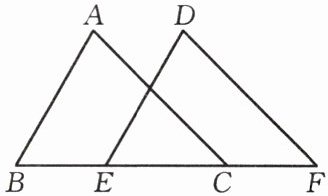
问题 如图,$AB = DE$,$AC = DF$,$B$,$E$,$C$,$F$在同一条直线上,$BE = CF$。求证:$AB// DE$。
名师指导
要证明$AB// DE$,可证$\angle B= \angle DEF$,可通过$\triangle ABC\cong\triangle DEF$证得。
解题示范(学生在教师指导下,独立完成)
证明:
名师指导
要证明$AB// DE$,可证$\angle B= \angle DEF$,可通过$\triangle ABC\cong\triangle DEF$证得。
解题示范(学生在教师指导下,独立完成)
证明:

答案:证明:
因为$BE = CF$,
所以$BE + EC = CF + EC$,
即$BC = EF$。
在$\triangle ABC$和$\triangle DEF$中,
$AB = DE$,$AC = DF$,$BC = EF$。
所以$\triangle ABC\cong\triangle DEF(SSS)$。
所以$\angle B=\angle DEF$。
所以$AB// DE$。
因为$BE = CF$,
所以$BE + EC = CF + EC$,
即$BC = EF$。
在$\triangle ABC$和$\triangle DEF$中,
$AB = DE$,$AC = DF$,$BC = EF$。
所以$\triangle ABC\cong\triangle DEF(SSS)$。
所以$\angle B=\angle DEF$。
所以$AB// DE$。
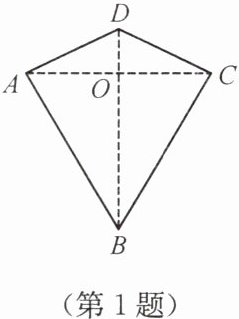
1. 两组邻边分别相等的四边形叫作“筝形”。如图,四边形$ABCD$是一个筝形,其中$AD = CD$,$AB = CB$,某学生在探究筝形的性质时,得到如下结论:(1)$AC\perp BD$;(2)$AO = CO= \frac{1}{2}AC$;(3)$\triangle ABD\cong\triangle CBD$。
其中正确的结论有(
A.$0$个
B.$1$个
C.$2$个
D.$3$个
其中正确的结论有(
D
)
A.$0$个
B.$1$个
C.$2$个
D.$3$个
答案:D
解析:
证明:
在$\triangle ABD$和$\triangle CBD$中,
$\left\{\begin{array}{l}AD=CD\\AB=CB\\BD=BD\end{array}\right.$
$\therefore\triangle ABD\cong\triangle CBD(SSS)$,故
(3)正确。
$\therefore\angle ABD=\angle CBD$。
在$\triangle ABO$和$\triangle CBO$中,
$\left\{\begin{array}{l}AB=CB\\\angle ABO=\angle CBO\\BO=BO\end{array}\right.$
$\therefore\triangle ABO\cong\triangle CBO(SAS)$。
$\therefore AO=CO=\frac{1}{2}AC$,$\angle AOB=\angle COB$,故
(2)正确。
$\because\angle AOB+\angle COB=180°$,
$\therefore\angle AOB=\angle COB=90°$,即$AC\perp BD$,故
(1)正确。
综上,正确的结论有3个。
D
在$\triangle ABD$和$\triangle CBD$中,
$\left\{\begin{array}{l}AD=CD\\AB=CB\\BD=BD\end{array}\right.$
$\therefore\triangle ABD\cong\triangle CBD(SSS)$,故
(3)正确。
$\therefore\angle ABD=\angle CBD$。
在$\triangle ABO$和$\triangle CBO$中,
$\left\{\begin{array}{l}AB=CB\\\angle ABO=\angle CBO\\BO=BO\end{array}\right.$
$\therefore\triangle ABO\cong\triangle CBO(SAS)$。
$\therefore AO=CO=\frac{1}{2}AC$,$\angle AOB=\angle COB$,故
(2)正确。
$\because\angle AOB+\angle COB=180°$,
$\therefore\angle AOB=\angle COB=90°$,即$AC\perp BD$,故
(1)正确。
综上,正确的结论有3个。
D
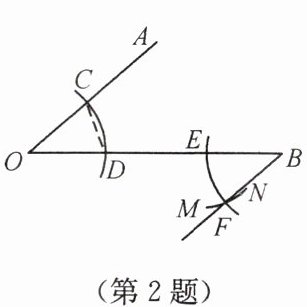
2. 如图,用尺规作出$\angle OBF= \angle AOB$,作图痕迹$\overset{\frown}{MN}$是(
A.以点$B$为圆心,$OD$为半径的弧
B.以点$B$为圆心,$DC$为半径的弧
C.以点$E$为圆心,$OD$为半径的弧
D.以点$E$为圆心,$DC$为半径的弧
D
)
A.以点$B$为圆心,$OD$为半径的弧
B.以点$B$为圆心,$DC$为半径的弧
C.以点$E$为圆心,$OD$为半径的弧
D.以点$E$为圆心,$DC$为半径的弧
答案:D
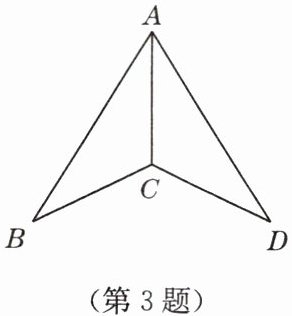
3. 如图,$AB = AD$,$CB = CD$,$\angle B = 30^{\circ}$,$\angle BAD = 46^{\circ}$,则$\angle ACD$的度数是(
A.$120^{\circ}$
B.$125^{\circ}$
C.$127^{\circ}$
D.$104^{\circ}$
C
)
A.$120^{\circ}$
B.$125^{\circ}$
C.$127^{\circ}$
D.$104^{\circ}$
答案:C
解析:
证明:连接AC。
在△ABC和△ADC中,
$\left\{\begin{array}{l}AB = AD \\CB = CD \\AC = AC\end{array}\right.$
∴△ABC≌△ADC(SSS)。
∴∠D=∠B=30°,∠CAD=∠CAB=$\frac{1}{2}$∠BAD=23°。
在△ACD中,∠ACD=180°-∠CAD-∠D=180°-23°-30°=127°。
C
在△ABC和△ADC中,
$\left\{\begin{array}{l}AB = AD \\CB = CD \\AC = AC\end{array}\right.$
∴△ABC≌△ADC(SSS)。
∴∠D=∠B=30°,∠CAD=∠CAB=$\frac{1}{2}$∠BAD=23°。
在△ACD中,∠ACD=180°-∠CAD-∠D=180°-23°-30°=127°。
C
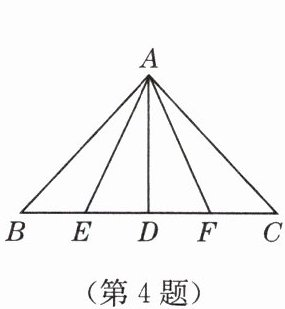
4. 如图,在$\triangle ABC$中,$AB = AC$,$E$,$D$,$F是BC$边的四等分点,$AE = AF$,则图中全等三角形共有(
A.$1$对
B.$2$对
C.$3$对
D.$4$对
D
)
A.$1$对
B.$2$对
C.$3$对
D.$4$对
答案:D
解析:
证明:
∵$AB=AC$,
∴$\triangle ABC$是等腰三角形,$\angle B=\angle C$。
∵$E$,$D$,$F$是$BC$的四等分点,
∴$BE=ED=DF=FC$,$BD=EC$,$BF=EC$(此处应为$BF=BE+ED+DF=3BE$,$EC=ED+DF+FC=3BE$,故$BF=EC$)。
1. 在$\triangle ABE$和$\triangle ACF$中,
$\left\{\begin{array}{l}AB=AC\\\angle B=\angle C\\BE=CF\end{array}\right.$,
∴$\triangle ABE\cong\triangle ACF$(SAS)。
2. 在$\triangle ABD$和$\triangle ACD$中,
$\left\{\begin{array}{l}AB=AC\\AD=AD\\BD=CD\end{array}\right.$($D$为$BC$中点,$BD=CD$),
∴$\triangle ABD\cong\triangle ACD$(SSS)。
3. 在$\triangle AED$和$\triangle AFD$中,
$\left\{\begin{array}{l}AE=AF\\AD=AD\\ED=FD\end{array}\right.$,
∴$\triangle AED\cong\triangle AFD$(SSS)。
4. 在$\triangle ABF$和$\triangle ACE$中,
$\left\{\begin{array}{l}AB=AC\\\angle B=\angle C\\BF=CE\end{array}\right.$,
∴$\triangle ABF\cong\triangle ACE$(SAS)。
综上,全等三角形共4对。
答案:D
∵$AB=AC$,
∴$\triangle ABC$是等腰三角形,$\angle B=\angle C$。
∵$E$,$D$,$F$是$BC$的四等分点,
∴$BE=ED=DF=FC$,$BD=EC$,$BF=EC$(此处应为$BF=BE+ED+DF=3BE$,$EC=ED+DF+FC=3BE$,故$BF=EC$)。
1. 在$\triangle ABE$和$\triangle ACF$中,
$\left\{\begin{array}{l}AB=AC\\\angle B=\angle C\\BE=CF\end{array}\right.$,
∴$\triangle ABE\cong\triangle ACF$(SAS)。
2. 在$\triangle ABD$和$\triangle ACD$中,
$\left\{\begin{array}{l}AB=AC\\AD=AD\\BD=CD\end{array}\right.$($D$为$BC$中点,$BD=CD$),
∴$\triangle ABD\cong\triangle ACD$(SSS)。
3. 在$\triangle AED$和$\triangle AFD$中,
$\left\{\begin{array}{l}AE=AF\\AD=AD\\ED=FD\end{array}\right.$,
∴$\triangle AED\cong\triangle AFD$(SSS)。
4. 在$\triangle ABF$和$\triangle ACE$中,
$\left\{\begin{array}{l}AB=AC\\\angle B=\angle C\\BF=CE\end{array}\right.$,
∴$\triangle ABF\cong\triangle ACE$(SAS)。
综上,全等三角形共4对。
答案:D