5. 若$a$,$b$,$c为\triangle ABC$的三边长,且满足$\vert a - 4\vert + (b - 2)^2 = 0$,则$c$的值可以为(
A.$5$
B.$6$
C.$7$
D.$8$
A
)A.$5$
B.$6$
C.$7$
D.$8$
答案:A.
解析:
因为$\vert a - 4\vert + (b - 2)^2 = 0$,且$\vert a - 4\vert \geq 0$,$(b - 2)^2 \geq 0$,所以$a - 4 = 0$,$b - 2 = 0$,解得$a = 4$,$b = 2$。
根据三角形三边关系,两边之和大于第三边,两边之差小于第三边,可得$4 - 2 < c < 4 + 2$,即$2 < c < 6$。
选项中只有$5$满足$2 < 5 < 6$。
A.
根据三角形三边关系,两边之和大于第三边,两边之差小于第三边,可得$4 - 2 < c < 4 + 2$,即$2 < c < 6$。
选项中只有$5$满足$2 < 5 < 6$。
A.
6. 已知等腰三角形的周长是$18$,则腰长的取值范围是
$\frac{9}{2}<$腰长$<9$
.答案:$\frac{9}{2}<$腰长$<9$.
解析:
设等腰三角形的腰长为$x$,底边长为$y$。
因为等腰三角形的周长是$18$,所以$2x + y=18$,则$y = 18 - 2x$。
根据三角形的三边关系,两边之和大于第三边,可得:
$x + x>y$,即$2x>18 - 2x$,解得$x>\frac{9}{2}$;
$x + y>x$,即$y>0$,所以$18 - 2x>0$,解得$x<9$。
综上,腰长的取值范围是$\frac{9}{2} < x < 9$。
因为等腰三角形的周长是$18$,所以$2x + y=18$,则$y = 18 - 2x$。
根据三角形的三边关系,两边之和大于第三边,可得:
$x + x>y$,即$2x>18 - 2x$,解得$x>\frac{9}{2}$;
$x + y>x$,即$y>0$,所以$18 - 2x>0$,解得$x<9$。
综上,腰长的取值范围是$\frac{9}{2} < x < 9$。
7. 已知等腰三角形的一边长为$18$,腰长是底边长的$\frac{3}{4}$,试求此三角形的周长.
答案:45或60.
解析:
情况一:底边长为18,腰长为$18×\frac{3}{4}=\frac{27}{2}$。
$\frac{27}{2}+\frac{27}{2}=27>18$,能构成三角形。
周长为$\frac{27}{2}+\frac{27}{2}+18=45$。
情况二:腰长为18,底边长为$18÷\frac{3}{4}=24$。
$18+18=36>24$,能构成三角形。
周长为$18+18+24=60$。
此三角形的周长为45或60。
$\frac{27}{2}+\frac{27}{2}=27>18$,能构成三角形。
周长为$\frac{27}{2}+\frac{27}{2}+18=45$。
情况二:腰长为18,底边长为$18÷\frac{3}{4}=24$。
$18+18=36>24$,能构成三角形。
周长为$18+18+24=60$。
此三角形的周长为45或60。
8. 若$a$,$b$,$c$表示三角形的三边长,化简:$\vert a - b - c\vert + \vert b - c - a\vert + \vert c - a - b\vert$.
答案:$a+b+c$.
解析:
因为$a$,$b$,$c$是三角形的三边长,所以根据三角形三边关系,两边之和大于第三边,可得:
$a < b + c$,即$a - b - c < 0$;
$b < c + a$,即$b - c - a < 0$;
$c < a + b$,即$c - a - b < 0$。
则$\vert a - b - c\vert = -(a - b - c) = -a + b + c$;
$\vert b - c - a\vert = -(b - c - a) = -b + c + a$;
$\vert c - a - b\vert = -(c - a - b) = -c + a + b$。
所以原式$= (-a + b + c) + (-b + c + a) + (-c + a + b)$
$= (-a + a + a) + (b - b + b) + (c + c - c)$
$= a + b + c$。
$a + b + c$
$a < b + c$,即$a - b - c < 0$;
$b < c + a$,即$b - c - a < 0$;
$c < a + b$,即$c - a - b < 0$。
则$\vert a - b - c\vert = -(a - b - c) = -a + b + c$;
$\vert b - c - a\vert = -(b - c - a) = -b + c + a$;
$\vert c - a - b\vert = -(c - a - b) = -c + a + b$。
所以原式$= (-a + b + c) + (-b + c + a) + (-c + a + b)$
$= (-a + a + a) + (b - b + b) + (c + c - c)$
$= a + b + c$。
$a + b + c$
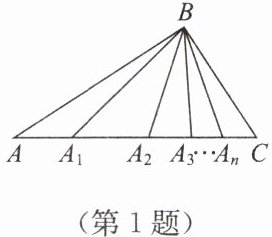
1. 如图,在$\triangle ABC$中,$A_1$,$A_2$,$A_3$,…,$A_n为AC边上不同的n$个点,首先连接$BA_1$,图中出现了$3$个不同的三角形,再连接$BA_2$,图中便有$6个不同的三角形……$
(1)完成下表:

(2)若出现了$45$个三角形,则共连接了多少个点?
(3)若一直连接到点$A_n$,则图中共有
(1)完成下表:

(2)若出现了$45$个三角形,则共连接了多少个点?
(3)若一直连接到点$A_n$,则图中共有
$\frac{1}{2}(n+1)(n+2)$
个三角形.(用含$n$的式子表示)
(1)10;15;21;28. (2)8个点. (3)$\frac{1}{2}(n+1)(n+2)$.
答案:
(1)10;15;21;28.
(2)8个点.
(3)$\frac{1}{2}(n+1)(n+2)$.
(1)10;15;21;28.
(2)8个点.
(3)$\frac{1}{2}(n+1)(n+2)$.
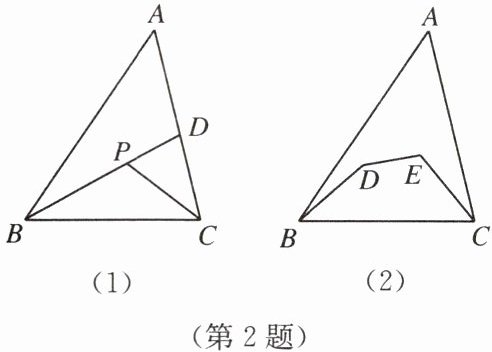
2. 如图(1),点$P是\triangle ABC$内部一点,连接$BP$,并延长交$AC于点D$.
(1)试探究$AB + BC + CA与2BD$的大小关系;
(2)试探究$AB + AC与PB + PC$的大小关系;
(3)如图(2),点$D$,$E是\triangle ABC$内部两点,试探究$AB + AC与BD + DE + CE$的大小关系.
(1)试探究$AB + BC + CA与2BD$的大小关系;
(2)试探究$AB + AC与PB + PC$的大小关系;
(3)如图(2),点$D$,$E是\triangle ABC$内部两点,试探究$AB + AC与BD + DE + CE$的大小关系.

答案:
(1)$AB+BC+CA>2BD$,理由:$\because AB+AD>BD$,$BC+CD>BD$,$\therefore AB+AD+BC+CD>BD+BD$,即$AB+BC+CA>2BD$.
(2)$AB+AC>PB+PC$,理由:在$\triangle ABD$中,$AB+AD>BP+PD$;在$\triangle PDC$中,$PD+DC>PC$,两式相加,得$AB+AD+PD+DC>BP+PD+PC$,即$AB+AC>PB+PC$.
(3)$AB+AC>BD+DE+CE$,理由:如图,延长$BD$交$CE$的延长线于点$G$,交$AC$于点$F$.在$\triangle ABF$中,$AB+AF>BD+DG+GF$,①在$\triangle GFC$中,$GF+AC - AF>GE+EC$,②在$\triangle DEG$中,$DG+GE>DE$,③①+②+③,得$AB+AC>BD+DE+CE$.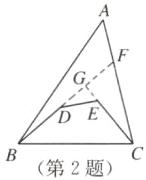
(1)$AB+BC+CA>2BD$,理由:$\because AB+AD>BD$,$BC+CD>BD$,$\therefore AB+AD+BC+CD>BD+BD$,即$AB+BC+CA>2BD$.
(2)$AB+AC>PB+PC$,理由:在$\triangle ABD$中,$AB+AD>BP+PD$;在$\triangle PDC$中,$PD+DC>PC$,两式相加,得$AB+AD+PD+DC>BP+PD+PC$,即$AB+AC>PB+PC$.
(3)$AB+AC>BD+DE+CE$,理由:如图,延长$BD$交$CE$的延长线于点$G$,交$AC$于点$F$.在$\triangle ABF$中,$AB+AF>BD+DG+GF$,①在$\triangle GFC$中,$GF+AC - AF>GE+EC$,②在$\triangle DEG$中,$DG+GE>DE$,③①+②+③,得$AB+AC>BD+DE+CE$.
