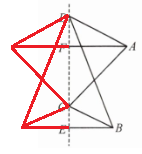
1. 在△ABC中,∠C= 90°,AB的垂直平分线交直线BC于点D,若∠BAD-∠DAC= 22.5°,则∠B等于(
A.37.5°
B.67.5°
C.37.5°或67.5°
D.无法确定
C
)A.37.5°
B.67.5°
C.37.5°或67.5°
D.无法确定
答案:C
解析:
∵AB的垂直平分线交直线BC于点D,
∴AD=BD,∠BAD=∠B。
设∠B=∠BAD=x,则∠DAC=x-22.5°。
∠C=90°,∠BAC+∠B=90°,即(x+x-22.5°)+x=90°或(x-(x-22.5°))+x=90°。
情况1:3x-22.5°=90°,解得x=37.5°。
情况2:22.5°+x=90°,解得x=67.5°。
∠B=37.5°或67.5°。
C
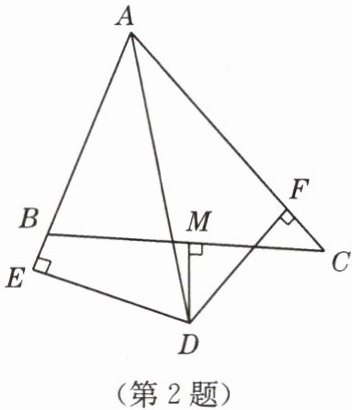
2. 如图,在△ABC中,∠BAC= 60°,∠BAC的平分线AD与边BC的垂直平分线相交于点D,DE⊥AB交AB的延长线于点E,DF⊥AC于点F. 现有下列结论:
①DE= DF;②DE+DF= AD;③DM平分∠EDF;④AB+AC= 2AE.
其中正确的有
①DE= DF;②DE+DF= AD;③DM平分∠EDF;④AB+AC= 2AE.
其中正确的有
①②④
(填序号).
答案:①②④
解析:
证明:
①
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,①正确;
②
∵∠BAC=60°,AD平分∠BAC,
∴∠EAD=∠FAD=30°,在Rt△AED中,DE=AD·sin30°=$\frac{1}{2}$AD,同理DF=$\frac{1}{2}$AD,
∴DE+DF=AD,②正确;
④连接BD、CD,
∵DM垂直平分BC,
∴BD=CD,在Rt△BED和Rt△CFD中,$\left\{\begin{array}{l}BD=CD\\ DE=DF\end{array}\right.$,
∴Rt△BED≌Rt△CFD(HL),
∴BE=CF,
∵AE=AF,AE=AB+BE,AF=AC-CF,
∴AE+AF=AB+AC+BE-CF,又
∵BE=CF,AE=AF,
∴2AE=AB+AC,④正确;
③假设DM平分∠EDF,则∠EDM=∠FDM,
∵DE⊥AB,DM⊥BC,
∴∠DEB=∠DMB=90°,∠EDM=∠EBD,同理∠FDM=∠FCD,
∴∠EBD=∠FCD,
∵∠EBD=∠ABC+90°,∠FCD=∠ACB+90°,
∴∠ABC=∠ACB,仅当AB=AC时成立,③错误;
综上,正确的有①②④。
①②④
①
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,①正确;
②
∵∠BAC=60°,AD平分∠BAC,
∴∠EAD=∠FAD=30°,在Rt△AED中,DE=AD·sin30°=$\frac{1}{2}$AD,同理DF=$\frac{1}{2}$AD,
∴DE+DF=AD,②正确;
④连接BD、CD,
∵DM垂直平分BC,
∴BD=CD,在Rt△BED和Rt△CFD中,$\left\{\begin{array}{l}BD=CD\\ DE=DF\end{array}\right.$,
∴Rt△BED≌Rt△CFD(HL),
∴BE=CF,
∵AE=AF,AE=AB+BE,AF=AC-CF,
∴AE+AF=AB+AC+BE-CF,又
∵BE=CF,AE=AF,
∴2AE=AB+AC,④正确;
③假设DM平分∠EDF,则∠EDM=∠FDM,
∵DE⊥AB,DM⊥BC,
∴∠DEB=∠DMB=90°,∠EDM=∠EBD,同理∠FDM=∠FCD,
∴∠EBD=∠FCD,
∵∠EBD=∠ABC+90°,∠FCD=∠ACB+90°,
∴∠ABC=∠ACB,仅当AB=AC时成立,③错误;
综上,正确的有①②④。
①②④
1. 如果点A与点B是关于直线l的对称点,则线段AB的垂直平分线是
直线 l.
.答案:直线 l.
2. 由一个平面图形可以得到它关于某直线对称的图形,这个图形与原图形的
形状
、大小
完全一样.答案:形状;大小.
3. 如图,△ABC关于直线l进行轴对称变换后,得到△A′B′C′,则l是AA′的
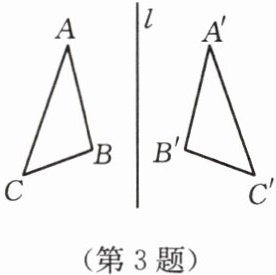
垂直平分线.

答案:垂直平分线.
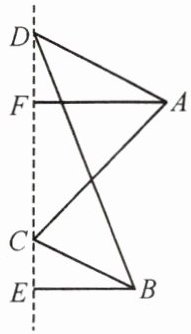
问题 如图,只画出了一个轴对称图形的一半(虚线为对称轴),请画出它的另一半.
名师指导
要补全一个轴对称图形,只需画出特殊点的对称点,然后依次连接各对称点,便可得到整个对称图形.
解题示范(学生在教师指导下,独立完成)
解:
名师指导
要补全一个轴对称图形,只需画出特殊点的对称点,然后依次连接各对称点,便可得到整个对称图形.
解题示范(学生在教师指导下,独立完成)
解:

答案: