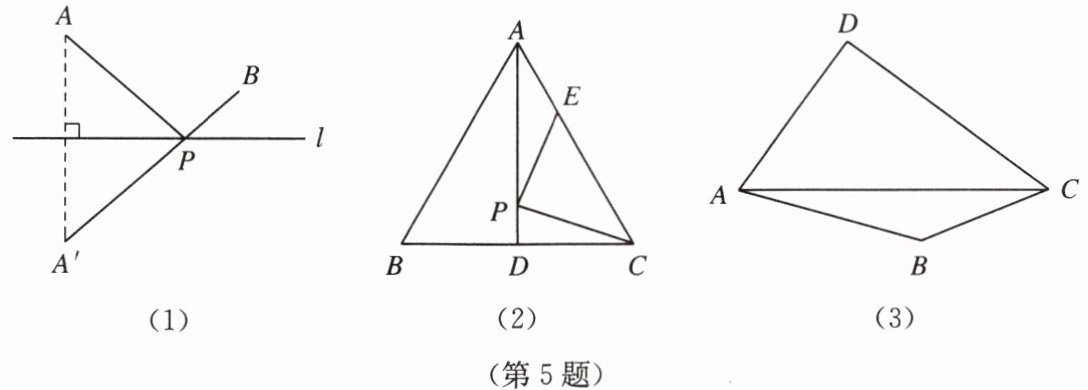
5. 【新知理解】如图(1),若点A,B在直线l同侧,在直线l上找一点P,使AP+BP的值最小.
作法:作点A关于直线l的对称点A′,连接A′B交直线l于点P,则点P即为所求.
【解决问题】如图(2),AD是等边三角形ABC的中线,AD= 6 cm,点P,E分别为AD,AC上的动点,则PC+PE的最小值为______ cm.
【拓展研究】如图(3),在四边形ABCD的对角线AC上找一点P,使∠APB= ∠APD.(保留作图痕迹,并对作图方法进行说明)
作法:作点A关于直线l的对称点A′,连接A′B交直线l于点P,则点P即为所求.
【解决问题】如图(2),AD是等边三角形ABC的中线,AD= 6 cm,点P,E分别为AD,AC上的动点,则PC+PE的最小值为______ cm.
【拓展研究】如图(3),在四边形ABCD的对角线AC上找一点P,使∠APB= ∠APD.(保留作图痕迹,并对作图方法进行说明)

答案:
[解决问题]如图
(1),作点 E 关于AD的对称点 F,连接 PF,则 PE=PF. 当点 F,P,C 在一条直线上时,PC+PE=PC+PF=CF(最短),当 CF⊥AB 时,CF 最短,CF=AD=6 cm. (2)[拓展研究]方法1:如图
(2),作点 B 关于 AC 的对称点 E,连接 DE 并延长,交 AC 于点 P,点 P 即为所求,连接 BP,则∠APB=∠APD. 方法2:作点 D 关于 AC 的对称点 D',连接 D'B 并延长与 AC 交于点 P,点 P 即为所求,连接 DP,则∠APB=∠APD.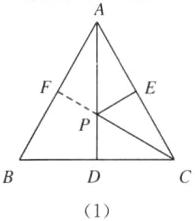
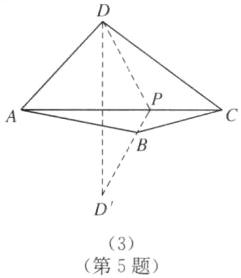
[解决问题]如图
(1),作点 E 关于AD的对称点 F,连接 PF,则 PE=PF. 当点 F,P,C 在一条直线上时,PC+PE=PC+PF=CF(最短),当 CF⊥AB 时,CF 最短,CF=AD=6 cm. (2)[拓展研究]方法1:如图
(2),作点 B 关于 AC 的对称点 E,连接 DE 并延长,交 AC 于点 P,点 P 即为所求,连接 BP,则∠APB=∠APD. 方法2:作点 D 关于 AC 的对称点 D',连接 D'B 并延长与 AC 交于点 P,点 P 即为所求,连接 DP,则∠APB=∠APD.


如图,在4×4正方形网格中,黑色部分的图形构成一个轴对称图形,现在任意选取一个白色的小正方形并涂黑,使所有黑色部分的图形仍然构成一个轴对称图形,则符合条件的白色小正方形的个数有______个.


答案:
提示:如图所示,有5个.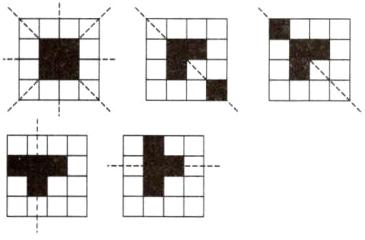
提示:如图所示,有5个.

1. 已知点A(-3,-4)平移后能与原来的位置关于y轴对称,则应把点A(
A.向左平移6个单位长度
B.向右平移6个单位长度
C.向下平移8个单位长度
D.向上平移8个单位长度
B
)A.向左平移6个单位长度
B.向右平移6个单位长度
C.向下平移8个单位长度
D.向上平移8个单位长度
答案:B.
解析:
点A(-3,-4)关于y轴对称的点的坐标为(3,-4)。
3 - (-3) = 6,所以应把点A向右平移6个单位长度。
B.
3 - (-3) = 6,所以应把点A向右平移6个单位长度。
B.
2. 在平面直角坐标系中,点P(-2,3)关于y轴对称的点的坐标为
(2,3)
.答案:(2,3)
3. 点A(-2,-1)与点B(2,-1)关于
y
轴对称.答案:y.
问题(1)利用平面直角坐标系,分别写出点(2,2),(-2,3),(4,-1)关于直线x= 1对称的点的坐标;
(2)分别写出(1)中各点关于直线x= -1对称的点的坐标;
(3)写出点(a,b)关于直线x= m对称的点的坐标.
名师指导
问题(1)(2)可先在平面直角坐标系中画出已知点和它们的对称点,再写出坐标.
问题(3)可观察和分析(1)(2)中各对对称点坐标之间的关系,总结、归纳出规律.
解题示范(学生在教师指导下,独立完成)
解:
(2)分别写出(1)中各点关于直线x= -1对称的点的坐标;
(3)写出点(a,b)关于直线x= m对称的点的坐标.
名师指导
问题(1)(2)可先在平面直角坐标系中画出已知点和它们的对称点,再写出坐标.
问题(3)可观察和分析(1)(2)中各对对称点坐标之间的关系,总结、归纳出规律.
解题示范(学生在教师指导下,独立完成)
解:
答案:(1) 点(2,2)关于直线x=1对称的点:横坐标为2×1 - 2=0,坐标(0,2);
点(-2,3)关于直线x=1对称的点:横坐标为2×1 - (-2)=4,坐标(4,3);
点(4,-1)关于直线x=1对称的点:横坐标为2×1 - 4=-2,坐标(-2,-1)。
(2) 点(2,2)关于直线x=-1对称的点:横坐标为2×(-1) - 2=-4,坐标(-4,2);
点(-2,3)关于直线x=-1对称的点:横坐标为2×(-1) - (-2)=0,坐标(0,3);
点(4,-1)关于直线x=-1对称的点:横坐标为2×(-1) - 4=-6,坐标(-6,-1)。
(3) 点(a,b)关于直线x=m对称的点的坐标为(2m - a, b)。
点(-2,3)关于直线x=1对称的点:横坐标为2×1 - (-2)=4,坐标(4,3);
点(4,-1)关于直线x=1对称的点:横坐标为2×1 - 4=-2,坐标(-2,-1)。
(2) 点(2,2)关于直线x=-1对称的点:横坐标为2×(-1) - 2=-4,坐标(-4,2);
点(-2,3)关于直线x=-1对称的点:横坐标为2×(-1) - (-2)=0,坐标(0,3);
点(4,-1)关于直线x=-1对称的点:横坐标为2×(-1) - 4=-6,坐标(-6,-1)。
(3) 点(a,b)关于直线x=m对称的点的坐标为(2m - a, b)。