1. 平面直角坐标系内的点A(-1,2)与点B(1,2)关于(
A.y轴对称
B.x轴对称
C.原点对称
D.直线y= x对称
A
)A.y轴对称
B.x轴对称
C.原点对称
D.直线y= x对称
答案:A.
解析:
点A(-1,2)与点B(1,2)的横坐标互为相反数,纵坐标相同,所以两点关于y轴对称。
A.
A.
2. 已知点M与点N(1,2)关于x轴对称,那么点M的坐标为(
A.(-1,2)
B.(1,2)
C.(-1,-2)
D.(1,-2)
D
)A.(-1,2)
B.(1,2)
C.(-1,-2)
D.(1,-2)
答案:D.
解析:
关于x轴对称的点,横坐标相同,纵坐标互为相反数。点N(1,2)关于x轴对称的点M的坐标为(1,-2)。
D.
D.
3. 如图,在平面直角坐标系xOy中,△ABC关于直线y= 1成轴对称,已知点A的坐标是(4,4),则点B的坐标是(
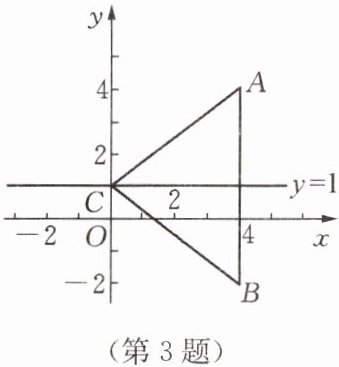
A.(4,-4)
B.(-4,2)
C.(4,-2)
D.(-2,4)
C
)
A.(4,-4)
B.(-4,2)
C.(4,-2)
D.(-2,4)
答案:C.
解析:
解:
∵△ABC关于直线$y=1$成轴对称,点$A$与点$B$是对称点,
∴点$A$与点$B$的横坐标相同,纵坐标关于直线$y=1$对称。
设点$B$的坐标为$(4, b)$,
则$\frac{4 + b}{2}=1$,
解得$b = -2$,
∴点$B$的坐标是$(4, -2)$。
C.
∵△ABC关于直线$y=1$成轴对称,点$A$与点$B$是对称点,
∴点$A$与点$B$的横坐标相同,纵坐标关于直线$y=1$对称。
设点$B$的坐标为$(4, b)$,
则$\frac{4 + b}{2}=1$,
解得$b = -2$,
∴点$B$的坐标是$(4, -2)$。
C.
4. 已知点A(m,2)与点B(1,n)关于x轴对称,那么m-n的值等于(
A.-1
B.1
C.-3
D.3
D
)A.-1
B.1
C.-3
D.3
答案:D.
解析:
∵点A(m,2)与点B(1,n)关于x轴对称,
∴m=1,n=-2,
∴m-n=1-(-2)=3.
D.
5. 已知$P_1(a-1,5)$和$P_2(2,b-1)$关于x轴对称,则$-(a+b)^2⁰^2^5$的值为
1
.答案:1.
解析:
因为点$P_1(a - 1, 5)$和$P_2(2, b - 1)$关于$x$轴对称,所以横坐标相等,纵坐标互为相反数。
可得$a - 1 = 2$,解得$a = 3$;$b - 1 = -5$,解得$b = -4$。
则$a + b = 3 + (-4) = -1$,所以$-(a + b)^{2025} = -(-1)^{2025} = -(-1) = 1$。
1
可得$a - 1 = 2$,解得$a = 3$;$b - 1 = -5$,解得$b = -4$。
则$a + b = 3 + (-4) = -1$,所以$-(a + b)^{2025} = -(-1)^{2025} = -(-1) = 1$。
1
6. 如图,把一张矩形纸片ABCD沿EF折叠后,点A落在CD边上的点A′处,点B落在点B′处,若∠2= 40°,求图中∠1的度数.
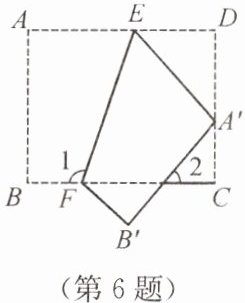

答案:115°.
解析:
解:
∵四边形ABCD是矩形,
∴AD//BC,
∴∠DEF=∠1。
由折叠性质得∠AEF=∠DEF,∠B'FC=∠2=40°。
设∠1=x,则∠AEF=∠DEF=x,
∴∠AED=180°-2x。
∵∠A'EB'=∠AEB=180°-∠1=180°-x,
∠A'EB'+∠B'FC=180°(A'E//B'F),
∴180°-x+40°=180°,
解得x=40°,矛盾。重新分析:
∵AD//BC,
∴∠A'EC=∠2=40°。
由折叠得∠AEF=∠A'EF,
设∠AEF=∠A'EF=y,则∠AED=180°-2y。
∵∠A'EC=∠AED=40°,
∴180°-2y=40°,解得y=70°。
∵AD//BC,
∴∠1=180°-∠AEF=180°-70°=115°。
答:∠1的度数为115°。
∵四边形ABCD是矩形,
∴AD//BC,
∴∠DEF=∠1。
由折叠性质得∠AEF=∠DEF,∠B'FC=∠2=40°。
设∠1=x,则∠AEF=∠DEF=x,
∴∠AED=180°-2x。
∵∠A'EB'=∠AEB=180°-∠1=180°-x,
∠A'EB'+∠B'FC=180°(A'E//B'F),
∴180°-x+40°=180°,
解得x=40°,矛盾。重新分析:
∵AD//BC,
∴∠A'EC=∠2=40°。
由折叠得∠AEF=∠A'EF,
设∠AEF=∠A'EF=y,则∠AED=180°-2y。
∵∠A'EC=∠AED=40°,
∴180°-2y=40°,解得y=70°。
∵AD//BC,
∴∠1=180°-∠AEF=180°-70°=115°。
答:∠1的度数为115°。