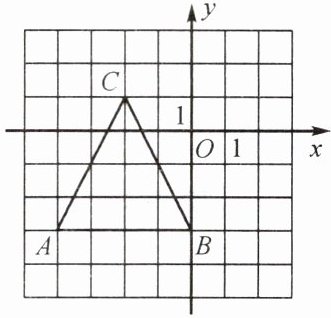
如图,已知△ABC的顶点坐标分别为A(-4,-3),B(0,-3),C(-2,1),现将点B向右平移2个单位长度后再向上平移4个单位长度到达点$B_1,$若设△ABC的面积为$S_1,△AB_1C$的面积为$S_2,$则$S_1,S_2$的大小关系为(
A. $S_1>S_2$
B. $S_1= S_2$
C. $S_1<S_2$
D. 无法确定
B
)A. $S_1>S_2$
B. $S_1= S_2$
C. $S_1<S_2$
D. 无法确定

答案:B.
解析:
解:
计算$S_1$:
$A(-4,-3)$,$B(0,-3)$,$AB$在直线$y=-3$上,
$AB$长度:$|0 - (-4)| = 4$,
点$C(-2,1)$到$AB$的距离($y$坐标差的绝对值):$|1 - (-3)| = 4$,
$S_1 = \frac{1}{2} × 4 × 4 = 8$。
计算$S_2$:
点$B$平移后得$B_1$:向右2个单位,向上4个单位,
$B_1$坐标:$(0+2, -3+4) = (2,1)$,
$A(-4,-3)$,$C(-2,1)$,$B_1(2,1)$,
$CB_1$在直线$y=1$上,长度:$|2 - (-2)| = 4$,
点$A$到$CB_1$的距离($y$坐标差的绝对值):$|1 - (-3)| = 4$,
$S_2 = \frac{1}{2} × 4 × 4 = 8$。
结论: $S_1 = S_2$。
答案:B.
计算$S_1$:
$A(-4,-3)$,$B(0,-3)$,$AB$在直线$y=-3$上,
$AB$长度:$|0 - (-4)| = 4$,
点$C(-2,1)$到$AB$的距离($y$坐标差的绝对值):$|1 - (-3)| = 4$,
$S_1 = \frac{1}{2} × 4 × 4 = 8$。
计算$S_2$:
点$B$平移后得$B_1$:向右2个单位,向上4个单位,
$B_1$坐标:$(0+2, -3+4) = (2,1)$,
$A(-4,-3)$,$C(-2,1)$,$B_1(2,1)$,
$CB_1$在直线$y=1$上,长度:$|2 - (-2)| = 4$,
点$A$到$CB_1$的距离($y$坐标差的绝对值):$|1 - (-3)| = 4$,
$S_2 = \frac{1}{2} × 4 × 4 = 8$。
结论: $S_1 = S_2$。
答案:B.
1. 等腰三角形的两个
底角
相等(简写成“等边对等角
”).答案:底角;等角.
2. 等腰三角形顶角的平分线平分
底边
,并且垂直于底边
.答案:底边;底边.
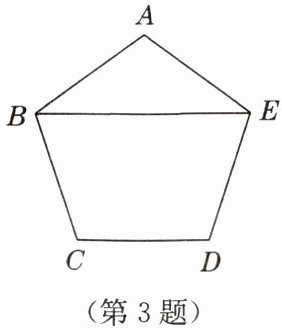
3. 如图,在正五边形 $ ABCDE $ 中,连接 $ BE $,则 $ \angle ABE $ 的度数为(
A.$ 30^{\circ} $
B.$ 36^{\circ} $
C.$ 54^{\circ} $
D.$ 72^{\circ} $
B
)
A.$ 30^{\circ} $
B.$ 36^{\circ} $
C.$ 54^{\circ} $
D.$ 72^{\circ} $
答案:B.
解析:
解:在正五边形$ABCDE$中,
$\because$正五边形内角和为$(5 - 2)×180^{\circ}=540^{\circ}$,
$\therefore$每个内角$\angle A=\frac{540^{\circ}}{5}=108^{\circ}$。
$\because AB = AE$,
$\therefore\triangle ABE$为等腰三角形,
$\therefore\angle ABE=\angle AEB=\frac{180^{\circ}-\angle A}{2}=\frac{180^{\circ}-108^{\circ}}{2}=36^{\circ}$。
答案:B.
$\because$正五边形内角和为$(5 - 2)×180^{\circ}=540^{\circ}$,
$\therefore$每个内角$\angle A=\frac{540^{\circ}}{5}=108^{\circ}$。
$\because AB = AE$,
$\therefore\triangle ABE$为等腰三角形,
$\therefore\angle ABE=\angle AEB=\frac{180^{\circ}-\angle A}{2}=\frac{180^{\circ}-108^{\circ}}{2}=36^{\circ}$。
答案:B.
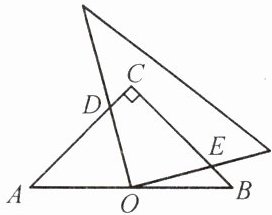
问题 如图,在等腰直角 $ \triangle ABC $ 中,$ \angle C = 90^{\circ} $,点 $ O $ 是 $ AB $ 的中点,且 $ AC = 3 $,将一块直角三角板的直角顶点放在点 $ O $ 处,始终保持该直角三角板的两直角边分别与 $ AC $,$ BC $ 相交,交点分别为 $ D $,$ E $,求 $ CD + CE $ 的值.
名师指导
连接 $ OC $ 构建全等三角形,证明 $ \triangle ODC \cong \triangle OEB $,得 $ DC = BE $,把 $ CD + CE $ 转化到同一条线段上,即求 $ BC $ 的长.
解题示范(学生在教师指导下,独立完成)
证明:

名师指导
连接 $ OC $ 构建全等三角形,证明 $ \triangle ODC \cong \triangle OEB $,得 $ DC = BE $,把 $ CD + CE $ 转化到同一条线段上,即求 $ BC $ 的长.
解题示范(学生在教师指导下,独立完成)
证明:
答案:3
解析:
连接OC。
∵△ABC是等腰直角三角形,∠C=90°,AC=3,
∴AC=BC=3,∠A=∠B=45°。
∵O是AB中点,
∴OC=OB,OC平分∠ACB,OC⊥AB,
∴∠OCD=∠BCO=45°=∠B,∠COB=90°。
∵∠DOE=90°,
∴∠DOE=∠COB,
∴∠DOC+∠COE=∠EOB+∠COE,
∴∠DOC=∠EOB。
在△ODC和△OEB中,
∠DOC=∠EOB,
OC=OB,
∠OCD=∠B,
∴△ODC≌△OEB(ASA),
∴DC=BE。
∴CD+CE=BE+CE=BC=3。
∵△ABC是等腰直角三角形,∠C=90°,AC=3,
∴AC=BC=3,∠A=∠B=45°。
∵O是AB中点,
∴OC=OB,OC平分∠ACB,OC⊥AB,
∴∠OCD=∠BCO=45°=∠B,∠COB=90°。
∵∠DOE=90°,
∴∠DOE=∠COB,
∴∠DOC+∠COE=∠EOB+∠COE,
∴∠DOC=∠EOB。
在△ODC和△OEB中,
∠DOC=∠EOB,
OC=OB,
∠OCD=∠B,
∴△ODC≌△OEB(ASA),
∴DC=BE。
∴CD+CE=BE+CE=BC=3。