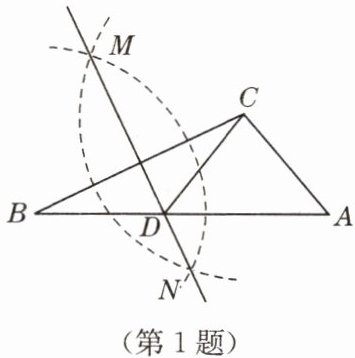
1. 如图,在已知的 $ \triangle ABC $ 中,按以下步骤作图:
① 分别以 $ B $,$ C $ 为圆心,以大于 $ \frac{1}{2}BC $ 的长为半径作弧,两弧相交于两点 $ M $,$ N $;
② 作直线 $ MN $ 交 $ AB $ 于点 $ D $,连接 $ CD $.
若 $ CD = AC $,$ \angle A = 50^{\circ} $,则 $ \angle ACB $ 的度数为(
A.$ 90^{\circ} $
B.$ 95^{\circ} $
C.$ 100^{\circ} $
D.$ 105^{\circ} $
① 分别以 $ B $,$ C $ 为圆心,以大于 $ \frac{1}{2}BC $ 的长为半径作弧,两弧相交于两点 $ M $,$ N $;
② 作直线 $ MN $ 交 $ AB $ 于点 $ D $,连接 $ CD $.
若 $ CD = AC $,$ \angle A = 50^{\circ} $,则 $ \angle ACB $ 的度数为(
D
)
A.$ 90^{\circ} $
B.$ 95^{\circ} $
C.$ 100^{\circ} $
D.$ 105^{\circ} $
答案:D.
解析:
证明:由作图步骤①②可知,MN是BC的垂直平分线,
∴DC=DB,
∴∠B=∠DCB。
∵CD=AC,∠A=50°,
∴∠CDA=∠A=50°。
∵∠CDA是△BCD的外角,
∴∠CDA=∠B+∠DCB=2∠B,
∴∠B=25°,
∴∠ACB=180°-∠A-∠B=180°-50°-25°=105°。
D.
∴DC=DB,
∴∠B=∠DCB。
∵CD=AC,∠A=50°,
∴∠CDA=∠A=50°。
∵∠CDA是△BCD的外角,
∴∠CDA=∠B+∠DCB=2∠B,
∴∠B=25°,
∴∠ACB=180°-∠A-∠B=180°-50°-25°=105°。
D.
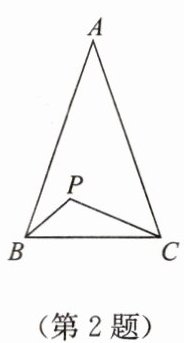
2. 如图,在 $ \triangle ABC $ 中,$ AB = AC $,$ P $ 是 $ \triangle ABC $ 内一点,且 $ \angle PBC = \angle PCA $,若 $ \angle BPC = 115^{\circ} $,则 $ \angle A $ 的度数为(
A.$ 50^{\circ} $
B.$ 55^{\circ} $
C.$ 60^{\circ} $
D.$ 65^{\circ} $
A
)
A.$ 50^{\circ} $
B.$ 55^{\circ} $
C.$ 60^{\circ} $
D.$ 65^{\circ} $
答案:A.
解析:
解:设$\angle PBC = \angle PCA = x$,$\angle PCB = y$。
因为$AB = AC$,所以$\angle ABC = \angle ACB$,则$\angle ABC = \angle ACB = x + y$。
在$\triangle BPC$中,$\angle BPC = 115^{\circ}$,所以$\angle PBC + \angle PCB = 180^{\circ} - 115^{\circ} = 65^{\circ}$,即$x + y = 65^{\circ}$,故$\angle ABC = \angle ACB = 65^{\circ}$。
在$\triangle ABC$中,$\angle A = 180^{\circ} - 2 × 65^{\circ} = 50^{\circ}$。
答案:A.
因为$AB = AC$,所以$\angle ABC = \angle ACB$,则$\angle ABC = \angle ACB = x + y$。
在$\triangle BPC$中,$\angle BPC = 115^{\circ}$,所以$\angle PBC + \angle PCB = 180^{\circ} - 115^{\circ} = 65^{\circ}$,即$x + y = 65^{\circ}$,故$\angle ABC = \angle ACB = 65^{\circ}$。
在$\triangle ABC$中,$\angle A = 180^{\circ} - 2 × 65^{\circ} = 50^{\circ}$。
答案:A.
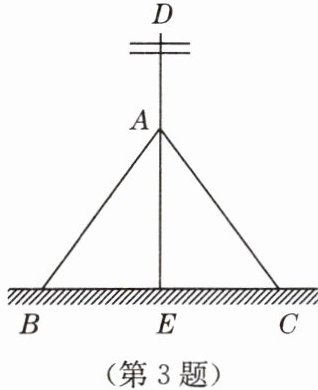
3. 如图,为了让电线杆垂直于地面,工程人员的操作方法通常是:从电线杆 $ DE $ 上一点 $ A $ 往地面拉两条长度相等的固定绳 $ AB $ 与 $ AC $,当固定点 $ B $,$ C $ 到杆脚 $ E $ 的距离相等,且 $ B $,$ E $,$ C $ 在同一条直线上时,电线杆 $ DE $ 就垂直于 $ BC $. 工程人员这种操作方法的依据是(
A.等边对等角
B.垂线段最短
C.等腰三角形“三线合一”
D.线段垂直平分线上的点到这条线段两端点的距离相等
C
)
A.等边对等角
B.垂线段最短
C.等腰三角形“三线合一”
D.线段垂直平分线上的点到这条线段两端点的距离相等
答案:C.