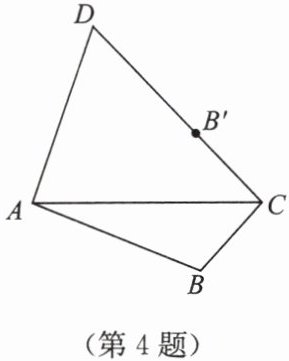
4. 如图,在四边形 $ ABCD $ 中,$ AB = AD $,点 $ B $ 关于 $ AC $ 的对称点 $ B' $ 恰好落在 $ CD $ 上,若 $ \angle BAD = \alpha $,则 $ \angle ACB $ 的度数为(
A.$ 45^{\circ} $
B.$ \alpha - 45^{\circ} $
C.$ \frac{1}{2}\alpha $
D.$ 90^{\circ} - \frac{1}{2}\alpha $
D
)
A.$ 45^{\circ} $
B.$ \alpha - 45^{\circ} $
C.$ \frac{1}{2}\alpha $
D.$ 90^{\circ} - \frac{1}{2}\alpha $
答案:D.
解析:
证明:连接$AB'$,$BB'$,设$AC$与$BB'$交于点$O$。
∵点$B$与$B'$关于$AC$对称,
∴$AC\perp BB'$,$OB=OB'$,$AB=AB'$,$\angle BAC=\angle B'AC$。
∵$AB=AD$,
∴$AD=AB'$,
∴$\angle ADB'=\angle AB'D$。
设$\angle BAC=\angle B'AC=x$,$\angle ACB=\angle ACB'=y$,
则$\angle AB'D=\angle BAC+\angle ACB'=x+y$,
$\angle ADB'=x+y$。
在$\triangle ADC$中,$\angle DAC=\angle BAD-\angle BAC=\alpha -x$,
$\angle ADC+\angle DAC+\angle ACD=180°$,
即$(x+y)+(\alpha -x)+y=180°$,
化简得$\alpha +2y=180°$,
解得$y=90° -\frac{1}{2}\alpha$,
即$\angle ACB=90° -\frac{1}{2}\alpha$。
D.
∵点$B$与$B'$关于$AC$对称,
∴$AC\perp BB'$,$OB=OB'$,$AB=AB'$,$\angle BAC=\angle B'AC$。
∵$AB=AD$,
∴$AD=AB'$,
∴$\angle ADB'=\angle AB'D$。
设$\angle BAC=\angle B'AC=x$,$\angle ACB=\angle ACB'=y$,
则$\angle AB'D=\angle BAC+\angle ACB'=x+y$,
$\angle ADB'=x+y$。
在$\triangle ADC$中,$\angle DAC=\angle BAD-\angle BAC=\alpha -x$,
$\angle ADC+\angle DAC+\angle ACD=180°$,
即$(x+y)+(\alpha -x)+y=180°$,
化简得$\alpha +2y=180°$,
解得$y=90° -\frac{1}{2}\alpha$,
即$\angle ACB=90° -\frac{1}{2}\alpha$。
D.
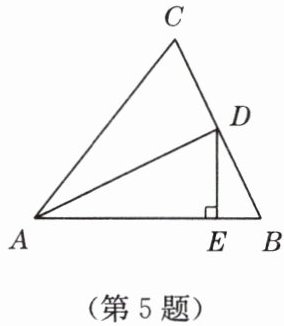
5. 如图,在 $ \triangle ABC $ 中,$ AB = AC $,$ D $ 为 $ BC $ 边的中点,$ DE \perp AB $.
(1)求证:$ \angle BAC = 2\angle EDB $;
(2)若 $ AC = 6 $,$ DE = 2 $,求 $ \triangle ABC $ 的面积.
(1)求证:$ \angle BAC = 2\angle EDB $;
(2)若 $ AC = 6 $,$ DE = 2 $,求 $ \triangle ABC $ 的面积.

答案:
(1)
∵ AB=AC,D为BC边的中点,
∴ AD⊥BC,∠BAD=∠CAD=1/2∠BAC,
∴ ∠B+∠BAD=90°.
∵ DE⊥AB,
∴ ∠B+∠EDB=90°,
∴ ∠EDB=∠BAD=1/2∠BAC,即∠BAC=2∠EDB.
(2) S△ABC=12.
(1)
∵ AB=AC,D为BC边的中点,
∴ AD⊥BC,∠BAD=∠CAD=1/2∠BAC,
∴ ∠B+∠BAD=90°.
∵ DE⊥AB,
∴ ∠B+∠EDB=90°,
∴ ∠EDB=∠BAD=1/2∠BAC,即∠BAC=2∠EDB.
(2) S△ABC=12.
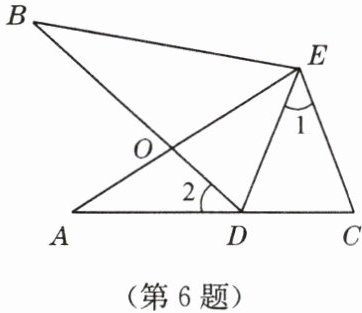
6. 如图,$ \angle A = \angle B $,$ AE = BE $,点 $ D $ 在 $ AC $ 边上,$ \angle 1 = \angle 2 $,$ AE $ 和 $ BD $ 相交于点 $ O $.
(1)求证:$ \triangle AEC \cong \triangle BED $;
(2)若 $ \angle 1 = 42^{\circ} $,求 $ \angle BDE $ 的度数.
(1)求证:$ \triangle AEC \cong \triangle BED $;
(2)若 $ \angle 1 = 42^{\circ} $,求 $ \angle BDE $ 的度数.

答案:
(1) 证明:
∵ AE和BD相交于点O,
∴ ∠AOD=∠BOE.在△AOD和△BOE中,∠A=∠B,
∴ ∠BEO=∠2.又
∵ ∠1=∠2,
∴ ∠1=∠BEO,
∴ ∠AEC=∠BED.在△AEC和△BED中,{∠A=∠B,AE=BE,∠AEC=∠BED,
∴ △AEC≌△BED(ASA).
(2)
∵ △AEC≌△BED,
∴ EC=ED,∠C=∠BDE.在△EDC中,
∵ EC=ED,∠1=42°,
∴ ∠C=∠EDC=69°,
∴ ∠BDE=∠C=69°.
(1) 证明:
∵ AE和BD相交于点O,
∴ ∠AOD=∠BOE.在△AOD和△BOE中,∠A=∠B,
∴ ∠BEO=∠2.又
∵ ∠1=∠2,
∴ ∠1=∠BEO,
∴ ∠AEC=∠BED.在△AEC和△BED中,{∠A=∠B,AE=BE,∠AEC=∠BED,
∴ △AEC≌△BED(ASA).
(2)
∵ △AEC≌△BED,
∴ EC=ED,∠C=∠BDE.在△EDC中,
∵ EC=ED,∠1=42°,
∴ ∠C=∠EDC=69°,
∴ ∠BDE=∠C=69°.
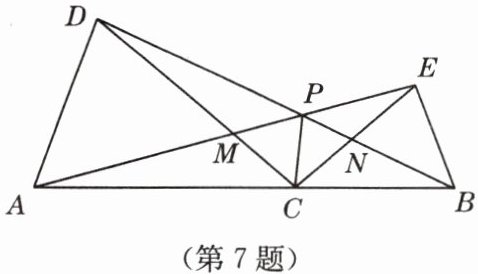
7. 如图,点 $ C $ 为线段 $ AB $ 上任意一点(不与点 $ A $,$ B $ 重合),分别以 $ AC $,$ BC $ 为一腰在 $ AB $ 的同侧作等腰 $ \triangle ACD $ 和 $ \triangle BCE $,$ CA = CD $,$ CB = CE $,$ \angle ACD $ 与 $ \angle BCE $ 都是锐角,且 $ \angle ACD = \angle BCE $,连接 $ AE $ 交 $ CD $ 于点 $ M $,连接 $ BD $ 交 $ CE $ 于点 $ N $,$ AE $ 与 $ BD $ 交于点 $ P $,连接 $ CP $. 求证:
(1)$ \triangle ACE \cong \triangle DCB $;
(2)$ \angle APC = \angle BPC $.
(1)$ \triangle ACE \cong \triangle DCB $;
(2)$ \angle APC = \angle BPC $.

答案:提示:
(1) 利用SAS得证;
(2) 由
(1)知,△ACE与△DCB面积相等,AE=BD,则AE,BD上的高相等,即点C到∠APB两边距离相等,得PC平分∠APB.
(1) 利用SAS得证;
(2) 由
(1)知,△ACE与△DCB面积相等,AE=BD,则AE,BD上的高相等,即点C到∠APB两边距离相等,得PC平分∠APB.