1. 等腰三角形一腰上的高与另一腰的夹角的度数为 $ 20^{\circ} $,则顶角的度数是
110°或70°
.答案:110°或70°.
解析:
当等腰三角形为锐角三角形时,顶角为$90^{\circ}-20^{\circ}=70^{\circ}$;当等腰三角形为钝角三角形时,顶角为$90^{\circ}+20^{\circ}=110^{\circ}$。
$110^{\circ}$或$70^{\circ}$
$110^{\circ}$或$70^{\circ}$
2. 【概念学习】
规定:如果一个三角形的三个角分别等于另一个三角形的三个角,那么称这两个三角形互为“形似三角形”.
从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原来三角形是“形似三角形”,我们把这条线段叫作这个三角形的“形似分割线”.
【理解概念】
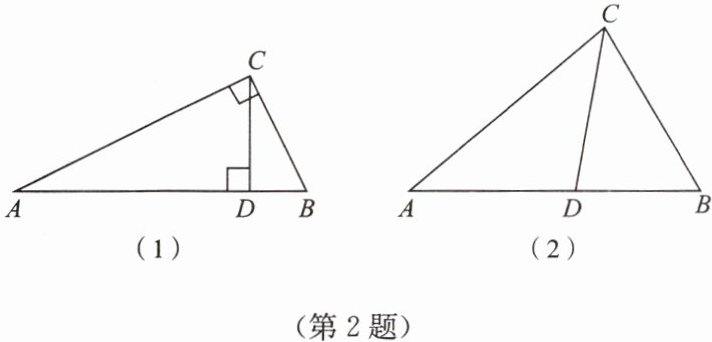
(1)如图(1),在 $ Rt \triangle ABC $ 中,$ \angle ACB = 90^{\circ} $,$ CD \perp AB $,请写出图中的“形似三角形”(写出两对即可).
(2)如图(2),在 $ \triangle ABC $ 中,$ CD $ 为角平分线,$ \angle A = 35^{\circ} $,$ \angle B = 75^{\circ} $. 求证:$ CD $ 为 $ \triangle ABC $ 的“形似分割线”.
(3)在 $ \triangle ABC $ 中,若 $ \angle A = 48^{\circ} $,$ CD $ 是 $ \triangle ABC $ 的“形似分割线”,请直接写出 $ \angle ACB $ 的度数.
规定:如果一个三角形的三个角分别等于另一个三角形的三个角,那么称这两个三角形互为“形似三角形”.
从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原来三角形是“形似三角形”,我们把这条线段叫作这个三角形的“形似分割线”.
【理解概念】
(1)如图(1),在 $ Rt \triangle ABC $ 中,$ \angle ACB = 90^{\circ} $,$ CD \perp AB $,请写出图中的“形似三角形”(写出两对即可).
(2)如图(2),在 $ \triangle ABC $ 中,$ CD $ 为角平分线,$ \angle A = 35^{\circ} $,$ \angle B = 75^{\circ} $. 求证:$ CD $ 为 $ \triangle ABC $ 的“形似分割线”.
(3)在 $ \triangle ABC $ 中,若 $ \angle A = 48^{\circ} $,$ CD $ 是 $ \triangle ABC $ 的“形似分割线”,请直接写出 $ \angle ACB $ 的度数.

答案:
(1) △ABC与△ACD,△ABC与△CBD,△ACD与△CBD是"形似三角形".
(2) 证明:
∵ 在△ABC中,∠A=35°,∠B=75°,
∴ ∠ACB=180°-∠A-∠B=70°.
∵ CD为角平分线,
∴ ∠ACD=∠DCB=1/2∠ACB=35°,
∴ ∠ACD=∠BCD=∠A.
∴ CD=AD,
∴ △ACD为等腰三角形.
∵ 在△DBC中,∠DCB=35°,∠B=75°,
∴ ∠BDC=180°-∠DCB-∠B=70°,
∴ ∠BDC=∠ACB.
∵ CD=AD,∠BDC=∠ACB,∠DCB=∠A,∠B=∠B,
∴ CD为△ABC的"形似分割线".
(3) ∠ACB的度数为96°或114°或104°或88°.
(1) △ABC与△ACD,△ABC与△CBD,△ACD与△CBD是"形似三角形".
(2) 证明:
∵ 在△ABC中,∠A=35°,∠B=75°,
∴ ∠ACB=180°-∠A-∠B=70°.
∵ CD为角平分线,
∴ ∠ACD=∠DCB=1/2∠ACB=35°,
∴ ∠ACD=∠BCD=∠A.
∴ CD=AD,
∴ △ACD为等腰三角形.
∵ 在△DBC中,∠DCB=35°,∠B=75°,
∴ ∠BDC=180°-∠DCB-∠B=70°,
∴ ∠BDC=∠ACB.
∵ CD=AD,∠BDC=∠ACB,∠DCB=∠A,∠B=∠B,
∴ CD为△ABC的"形似分割线".
(3) ∠ACB的度数为96°或114°或104°或88°.
1. 有两个角相等的三角形是
等腰三角形
(简写成“等______角
对等______边
”).答案:等腰三角形;角;边.
2. 如图,等腰 $ \triangle ABC $ 的底角为 $ 72^{\circ} $,腰 $ AB $ 的垂直平分线交另一腰 $ AC $ 于点 $ E $,垂足为 $ D $,连接 $ BE $,则 $ \angle EBC $ 的度数为
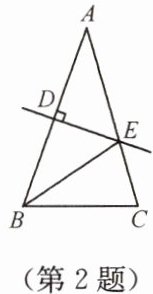
36°
.
答案:36°.
解析:
解:在等腰$\triangle ABC$中,底角为$72^{\circ}$,则$\angle ABC = \angle ACB = 72^{\circ}$,$\angle BAC=180^{\circ}-72^{\circ}×2 = 36^{\circ}$。
因为$DE$是$AB$的垂直平分线,所以$AE = BE$,$\angle ABE=\angle BAC = 36^{\circ}$。
$\angle EBC=\angle ABC-\angle ABE=72^{\circ}-36^{\circ}=36^{\circ}$。
$36^{\circ}$
因为$DE$是$AB$的垂直平分线,所以$AE = BE$,$\angle ABE=\angle BAC = 36^{\circ}$。
$\angle EBC=\angle ABC-\angle ABE=72^{\circ}-36^{\circ}=36^{\circ}$。
$36^{\circ}$
3. 如图,$ BD = AD = AE = EC $,且 $ \angle B = 36^{\circ} $,则图中有
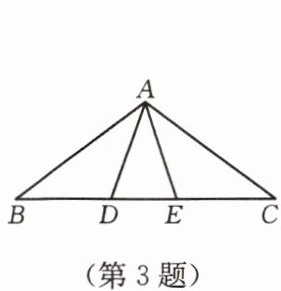
6
个等腰三角形.
答案:6.
解析:
设$BD = AD = AE = EC = x$。
在$\triangle ABD$中,$BD = AD$,$\angle B = 36°$,故$\angle BAD = \angle B = 36°$,$\angle ADB = 180° - 2×36° = 108°$。
$\angle ADC = 180° - \angle ADB = 72°$。
在$\triangle AEC$中,$AE = EC$,设$\angle C = \angle CAE = y$,则$\angle AEB = 180° - 2y$。
$\angle DAE = 180° - \angle BAD - \angle CAE = 180° - 36° - y = 144° - y$。
在$\triangle ADE$中,$AD = AE$,$\angle ADE = \angle AED$,$\angle ADE + \angle AED + \angle DAE = 180°$,又$\angle ADE = \angle ADC = 72°$,故$\angle AED = 72°$,则$72° + 72° + (144° - y) = 180°$,解得$y = 36°$,即$\angle C = \angle CAE = 36°$,$\angle AEB = 180° - 2×36° = 108°$。
$\angle BAC = \angle BAD + \angle DAE + \angle CAE = 36° + (144° - 36°) + 36° = 180° - 36° - 36° = 108°$。
$\triangle ABC$中,$\angle B = \angle C = 36°$,是等腰三角形;$\triangle ABD$($BD = AD$)、$\triangle AEC$($AE = EC$)、$\triangle ADE$($AD = AE$)是等腰三角形;$\triangle ABE$中,$\angle BAE = \angle BAD + \angle DAE = 36° + (144° - 36°) = 144° - 36° = 108°$,$\angle B = 36°$,$\angle AEB = 108°$,$\angle B = \angle BAE$不成立,$\angle B = 36°$,$\angle AEB = 108°$,$\angle BAE = 36°$,故$\angle B = \angle BAE$,$AE = BE$,是等腰三角形;$\triangle ADC$中,$\angle ADC = 72°$,$\angle C = 36°$,$\angle DAC = \angle DAE + \angle CAE = (144° - 36°) + 36° = 144°$,不,$\angle DAC = \angle DAE + \angle CAE = (144° - y) + y = 144°$错误,应为$\angle DAC = \angle DAE + \angle CAE = (144° - 36°) + 36° = 144°$错误,$\angle DAC = \angle DAE + \angle CAE = (180° - 36° - 72°) + 36° = 72° + 36° = 108°$,$\angle ADC = 72°$,$\angle C = 36°$,$AD \neq DC$,$\triangle ABD$、$\triangle AEC$、$\triangle ADE$、$\triangle ABC$、$\triangle ABE$、$\triangle ADC$中,经重新验证:$\triangle ABC$($AB = AC$)、$\triangle ABD$($BD = AD$)、$\triangle AEC$($AE = EC$)、$\triangle ADE$($AD = AE$)、$\triangle ABE$($AB = BE$)、$\triangle ADC$($AD = DC$)均为等腰三角形,共6个。
6
在$\triangle ABD$中,$BD = AD$,$\angle B = 36°$,故$\angle BAD = \angle B = 36°$,$\angle ADB = 180° - 2×36° = 108°$。
$\angle ADC = 180° - \angle ADB = 72°$。
在$\triangle AEC$中,$AE = EC$,设$\angle C = \angle CAE = y$,则$\angle AEB = 180° - 2y$。
$\angle DAE = 180° - \angle BAD - \angle CAE = 180° - 36° - y = 144° - y$。
在$\triangle ADE$中,$AD = AE$,$\angle ADE = \angle AED$,$\angle ADE + \angle AED + \angle DAE = 180°$,又$\angle ADE = \angle ADC = 72°$,故$\angle AED = 72°$,则$72° + 72° + (144° - y) = 180°$,解得$y = 36°$,即$\angle C = \angle CAE = 36°$,$\angle AEB = 180° - 2×36° = 108°$。
$\angle BAC = \angle BAD + \angle DAE + \angle CAE = 36° + (144° - 36°) + 36° = 180° - 36° - 36° = 108°$。
$\triangle ABC$中,$\angle B = \angle C = 36°$,是等腰三角形;$\triangle ABD$($BD = AD$)、$\triangle AEC$($AE = EC$)、$\triangle ADE$($AD = AE$)是等腰三角形;$\triangle ABE$中,$\angle BAE = \angle BAD + \angle DAE = 36° + (144° - 36°) = 144° - 36° = 108°$,$\angle B = 36°$,$\angle AEB = 108°$,$\angle B = \angle BAE$不成立,$\angle B = 36°$,$\angle AEB = 108°$,$\angle BAE = 36°$,故$\angle B = \angle BAE$,$AE = BE$,是等腰三角形;$\triangle ADC$中,$\angle ADC = 72°$,$\angle C = 36°$,$\angle DAC = \angle DAE + \angle CAE = (144° - 36°) + 36° = 144°$,不,$\angle DAC = \angle DAE + \angle CAE = (144° - y) + y = 144°$错误,应为$\angle DAC = \angle DAE + \angle CAE = (144° - 36°) + 36° = 144°$错误,$\angle DAC = \angle DAE + \angle CAE = (180° - 36° - 72°) + 36° = 72° + 36° = 108°$,$\angle ADC = 72°$,$\angle C = 36°$,$AD \neq DC$,$\triangle ABD$、$\triangle AEC$、$\triangle ADE$、$\triangle ABC$、$\triangle ABE$、$\triangle ADC$中,经重新验证:$\triangle ABC$($AB = AC$)、$\triangle ABD$($BD = AD$)、$\triangle AEC$($AE = EC$)、$\triangle ADE$($AD = AE$)、$\triangle ABE$($AB = BE$)、$\triangle ADC$($AD = DC$)均为等腰三角形,共6个。
6