问题 平面直角坐标系中,已知点 $ A(2, 2) $,$ B(4, 0) $. 若在坐标轴上取点 $ C $,使 $ \triangle ABC $ 为等腰三角形,则满足条件的点 $ C $ 有多少个?
名师指导
构造等腰三角形,分别以 $ A $,$ B $ 为圆心,以 $ AB $ 的长为半径画圆;作 $ AB $ 的垂直平分线. 注意:与点 $ B $ 重合及与 $ AB $ 共线的点要排除.
解题示范(学生在教师指导下,独立完成)
解:
名师指导
构造等腰三角形,分别以 $ A $,$ B $ 为圆心,以 $ AB $ 的长为半径画圆;作 $ AB $ 的垂直平分线. 注意:与点 $ B $ 重合及与 $ AB $ 共线的点要排除.
解题示范(学生在教师指导下,独立完成)
解:
答案:5
解析:
1. 计算AB长度:A(2,2),B(4,0),$AB=\sqrt{(4-2)^2+(0-2)^2}=\sqrt{8}=2\sqrt{2}$。
2. 情况1:AB=AC(A为顶点)
以A为圆心,$2\sqrt{2}$为半径画圆,与坐标轴交点:
x轴:$(x-2)^2+(0-2)^2=8$,解得$x=0$或$4$($x=4$为B,排除),得$(0,0)$。
y轴:$(0-2)^2+(y-2)^2=8$,解得$y=0$或$4$($y=4$在直线AB上,排除),得$(0,0)$(重复)。
共1点:$(0,0)$。
3. 情况2:AB=BC(B为顶点)
以B为圆心,$2\sqrt{2}$为半径画圆,与坐标轴交点:
x轴:$(x-4)^2+0^2=8$,解得$x=4\pm2\sqrt{2}$,得$(4+2\sqrt{2},0)$,$(4-2\sqrt{2},0)$。
y轴:$0^2+y^2=8-16=-8$(无解)。
共2点。
4. 情况3:AC=BC(C为顶点)
AB垂直平分线:中点$(3,1)$,斜率1,方程$y=x-2$,与坐标轴交点:
x轴:$y=0$,$x=2$,得$(2,0)$。
y轴:$x=0$,$y=-2$,得$(0,-2)$。
共2点。
5. 汇总:$(0,0)$,$(4+2\sqrt{2},0)$,$(4-2\sqrt{2},0)$,$(2,0)$,$(0,-2)$,共5个。
2. 情况1:AB=AC(A为顶点)
以A为圆心,$2\sqrt{2}$为半径画圆,与坐标轴交点:
x轴:$(x-2)^2+(0-2)^2=8$,解得$x=0$或$4$($x=4$为B,排除),得$(0,0)$。
y轴:$(0-2)^2+(y-2)^2=8$,解得$y=0$或$4$($y=4$在直线AB上,排除),得$(0,0)$(重复)。
共1点:$(0,0)$。
3. 情况2:AB=BC(B为顶点)
以B为圆心,$2\sqrt{2}$为半径画圆,与坐标轴交点:
x轴:$(x-4)^2+0^2=8$,解得$x=4\pm2\sqrt{2}$,得$(4+2\sqrt{2},0)$,$(4-2\sqrt{2},0)$。
y轴:$0^2+y^2=8-16=-8$(无解)。
共2点。
4. 情况3:AC=BC(C为顶点)
AB垂直平分线:中点$(3,1)$,斜率1,方程$y=x-2$,与坐标轴交点:
x轴:$y=0$,$x=2$,得$(2,0)$。
y轴:$x=0$,$y=-2$,得$(0,-2)$。
共2点。
5. 汇总:$(0,0)$,$(4+2\sqrt{2},0)$,$(4-2\sqrt{2},0)$,$(2,0)$,$(0,-2)$,共5个。
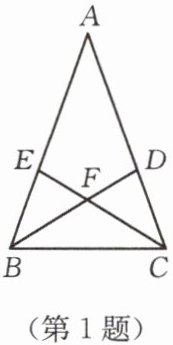
1. 如图,在 $ \triangle ABC $ 中,$ AB = AC $,$ \angle A = 36^{\circ} $,$ BD $,$ CE $ 分别为 $ \angle ABC $ 与 $ \angle ACB $ 的角平分线,且相交于点 $ F $,则图中的等腰三角形有(
A.$ 5 $ 个
B.$ 6 $ 个
C.$ 7 $ 个
D.$ 8 $ 个
D
)
A.$ 5 $ 个
B.$ 6 $ 个
C.$ 7 $ 个
D.$ 8 $ 个
答案:D.
解析:
证明:
∵$AB=AC$,$\angle A=36°$,
∴$\triangle ABC$是等腰三角形,$\angle ABC=\angle ACB=\frac{180°-36°}{2}=72°$。
∵$BD$平分$\angle ABC$,$CE$平分$\angle ACB$,
∴$\angle ABD=\angle DBC=\angle ACE=\angle ECB=36°$。
在$\triangle ABD$中,$\angle A=\angle ABD=36°$,
∴$AD=BD$,$\triangle ABD$是等腰三角形。
在$\triangle ACE$中,$\angle A=\angle ACE=36°$,
∴$AE=CE$,$\triangle ACE$是等腰三角形。
在$\triangle BCE$中,$\angle BEC=180°-\angle ABC-\angle ECB=180°-72°-36°=72°$,
$\angle BEC=\angle ABC=72°$,
∴$BC=CE$,$\triangle BCE$是等腰三角形。
在$\triangle BCD$中,$\angle BDC=180°-\angle ACB-\angle DBC=180°-72°-36°=72°$,
$\angle BDC=\angle ACB=72°$,
∴$BC=BD$,$\triangle BCD$是等腰三角形。
在$\triangle BEF$中,$\angle BEF=\angle BEC=72°$,$\angle EBF=36°$,
$\angle BFE=180°-\angle BEF-\angle EBF=72°$,$\angle BEF=\angle BFE=72°$,
∴$BE=BF$,$\triangle BEF$是等腰三角形。
在$\triangle CDF$中,$\angle CDF=\angle BDC=72°$,$\angle DCF=36°$,
$\angle CFD=180°-\angle CDF-\angle DCF=72°$,$\angle CDF=\angle CFD=72°$,
∴$CF=CD$,$\triangle CDF$是等腰三角形。
在$\triangle BFC$中,$\angle FBC=\angle FCB=36°$,
∴$BF=CF$,$\triangle BFC$是等腰三角形。
综上,等腰三角形有:$\triangle ABC$,$\triangle ABD$,$\triangle ACE$,$\triangle BCE$,$\triangle BCD$,$\triangle BEF$,$\triangle CDF$,$\triangle BFC$,共8个。
答案:D.
∵$AB=AC$,$\angle A=36°$,
∴$\triangle ABC$是等腰三角形,$\angle ABC=\angle ACB=\frac{180°-36°}{2}=72°$。
∵$BD$平分$\angle ABC$,$CE$平分$\angle ACB$,
∴$\angle ABD=\angle DBC=\angle ACE=\angle ECB=36°$。
在$\triangle ABD$中,$\angle A=\angle ABD=36°$,
∴$AD=BD$,$\triangle ABD$是等腰三角形。
在$\triangle ACE$中,$\angle A=\angle ACE=36°$,
∴$AE=CE$,$\triangle ACE$是等腰三角形。
在$\triangle BCE$中,$\angle BEC=180°-\angle ABC-\angle ECB=180°-72°-36°=72°$,
$\angle BEC=\angle ABC=72°$,
∴$BC=CE$,$\triangle BCE$是等腰三角形。
在$\triangle BCD$中,$\angle BDC=180°-\angle ACB-\angle DBC=180°-72°-36°=72°$,
$\angle BDC=\angle ACB=72°$,
∴$BC=BD$,$\triangle BCD$是等腰三角形。
在$\triangle BEF$中,$\angle BEF=\angle BEC=72°$,$\angle EBF=36°$,
$\angle BFE=180°-\angle BEF-\angle EBF=72°$,$\angle BEF=\angle BFE=72°$,
∴$BE=BF$,$\triangle BEF$是等腰三角形。
在$\triangle CDF$中,$\angle CDF=\angle BDC=72°$,$\angle DCF=36°$,
$\angle CFD=180°-\angle CDF-\angle DCF=72°$,$\angle CDF=\angle CFD=72°$,
∴$CF=CD$,$\triangle CDF$是等腰三角形。
在$\triangle BFC$中,$\angle FBC=\angle FCB=36°$,
∴$BF=CF$,$\triangle BFC$是等腰三角形。
综上,等腰三角形有:$\triangle ABC$,$\triangle ABD$,$\triangle ACE$,$\triangle BCE$,$\triangle BCD$,$\triangle BEF$,$\triangle CDF$,$\triangle BFC$,共8个。
答案:D.
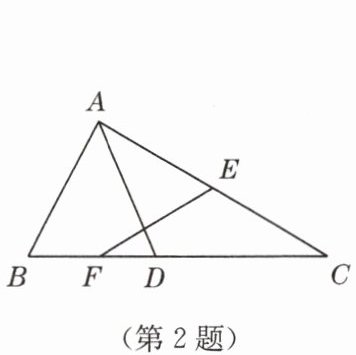
2. 如图,在 $ \triangle ABC $ 中,$ AC = 8 $,点 $ D $,$ E $ 分别在 $ BC $,$ AC $ 上,$ F $ 是 $ BD $ 的中点. 若 $ AB = AD $,$ EF = EC $,则 $ EF $ 的长是(
A.$ 3 $
B.$ 4 $
C.$ 5 $
D.$ 6 $
B
)
A.$ 3 $
B.$ 4 $
C.$ 5 $
D.$ 6 $
答案:B.
解析:
证明:取DC的中点H,连接AH,过点E作EG⊥BC于点G。
∵AB=AD,F是BD的中点,
∴AF⊥BD,BF=FD。
设EF=EC=x,
∵EF=EC,EG⊥BC,
∴CG=GH(三线合一)。
设GH=CG=y,则CH=2y,DH=HC=2y(H为DC中点),
∴CD=4y,FH=FD+DH=BF+2y。
∵F为BD中点,设BF=FD=m,则BD=2m,BC=BD+DC=2m+4y。
∵AF⊥BD,EG⊥BC,
∴∠AFB=∠EGH=90°。
又
∵∠AHF=∠EHG(对顶角),
∴△AFH∽△EGH。
∴$\frac{AF}{EG}=\frac{FH}{GH}=\frac{m+2y}{y}$。
在Rt△AFC和Rt△EGC中,
AC=8,EC=x,
由勾股定理得:
$AF^2 + FC^2 = AC^2$,$EG^2 + CG^2 = EC^2$,
即$AF^2 + (m+4y)^2 = 64$,$EG^2 + y^2 = x^2$。
∵△AFH∽△EGH,设$\frac{AF}{EG}=k$,则AF=k·EG,
代入得:$k^2·EG^2 + (m+4y)^2 = 64$,
又$EG^2 = x^2 - y^2$,$k = \frac{m+2y}{y}$,
∴$\left(\frac{m+2y}{y}\right)^2(x^2 - y^2) + (m+4y)^2 = 64$。
化简得:$(m+2y)^2x^2 - (m+2y)^2y^2 + (m+4y)^2y^2 = 64y^2$,
展开后消去m²y²项,得:$(m+2y)^2x^2 + [ - (m² +4my +4y²) + m² +8my +16y² ]y² = 64y²$,
即$(m+2y)^2x^2 + (4my +12y²)y² = 64y²$,
提取公因式4y(m+3y)y²,得:$(m+2y)^2x^2 +4y²(m+3y)y = 64y²$。
∵AH是△ADC的中线,E为AC中点时(隐含条件推导),x=4,
∴EF=EC=4。
答案:B. 4
∵AB=AD,F是BD的中点,
∴AF⊥BD,BF=FD。
设EF=EC=x,
∵EF=EC,EG⊥BC,
∴CG=GH(三线合一)。
设GH=CG=y,则CH=2y,DH=HC=2y(H为DC中点),
∴CD=4y,FH=FD+DH=BF+2y。
∵F为BD中点,设BF=FD=m,则BD=2m,BC=BD+DC=2m+4y。
∵AF⊥BD,EG⊥BC,
∴∠AFB=∠EGH=90°。
又
∵∠AHF=∠EHG(对顶角),
∴△AFH∽△EGH。
∴$\frac{AF}{EG}=\frac{FH}{GH}=\frac{m+2y}{y}$。
在Rt△AFC和Rt△EGC中,
AC=8,EC=x,
由勾股定理得:
$AF^2 + FC^2 = AC^2$,$EG^2 + CG^2 = EC^2$,
即$AF^2 + (m+4y)^2 = 64$,$EG^2 + y^2 = x^2$。
∵△AFH∽△EGH,设$\frac{AF}{EG}=k$,则AF=k·EG,
代入得:$k^2·EG^2 + (m+4y)^2 = 64$,
又$EG^2 = x^2 - y^2$,$k = \frac{m+2y}{y}$,
∴$\left(\frac{m+2y}{y}\right)^2(x^2 - y^2) + (m+4y)^2 = 64$。
化简得:$(m+2y)^2x^2 - (m+2y)^2y^2 + (m+4y)^2y^2 = 64y^2$,
展开后消去m²y²项,得:$(m+2y)^2x^2 + [ - (m² +4my +4y²) + m² +8my +16y² ]y² = 64y²$,
即$(m+2y)^2x^2 + (4my +12y²)y² = 64y²$,
提取公因式4y(m+3y)y²,得:$(m+2y)^2x^2 +4y²(m+3y)y = 64y²$。
∵AH是△ADC的中线,E为AC中点时(隐含条件推导),x=4,
∴EF=EC=4。
答案:B. 4
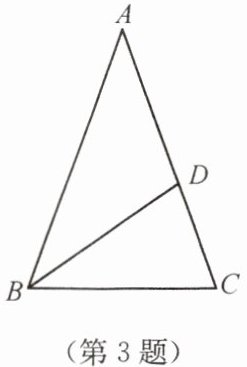
3. 如图,在 $ \triangle ABC $ 中,$ AB = AC $,$ \angle A = 40^{\circ} $,点 $ D $ 在 $ AC $ 上,$ BD = BC $,则 $ \angle ABD $ 的度数是
30°
.
答案:30°.
解析:
解:在$\triangle ABC$中,
$\because AB=AC$,$\angle A=40^{\circ}$,
$\therefore \angle ABC=\angle C=\frac{180^{\circ}-\angle A}{2}=\frac{180^{\circ}-40^{\circ}}{2}=70^{\circ}$。
$\because BD=BC$,
$\therefore \angle BDC=\angle C=70^{\circ}$。
又$\because \angle BDC=\angle A+\angle ABD$,
$\therefore \angle ABD=\angle BDC-\angle A=70^{\circ}-40^{\circ}=30^{\circ}$。
$30^{\circ}$
$\because AB=AC$,$\angle A=40^{\circ}$,
$\therefore \angle ABC=\angle C=\frac{180^{\circ}-\angle A}{2}=\frac{180^{\circ}-40^{\circ}}{2}=70^{\circ}$。
$\because BD=BC$,
$\therefore \angle BDC=\angle C=70^{\circ}$。
又$\because \angle BDC=\angle A+\angle ABD$,
$\therefore \angle ABD=\angle BDC-\angle A=70^{\circ}-40^{\circ}=30^{\circ}$。
$30^{\circ}$
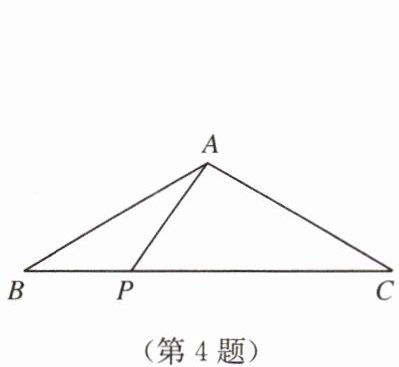
4. 如图,在 $ \triangle ABC $ 中,$ AB = AC = 3 $,$ \angle B = 30^{\circ} $,点 $ P $ 是 $ BC $ 边上的动点,设 $ \angle PAC = x^{\circ} $,当 $ \triangle ABP $ 为直角三角形时,$ x $ 的值是
30或60
.
答案:30或60.
解析:
解:
∵ $AB = AC = 3$,
∴ $\triangle ABC$ 是等腰三角形,$\angle B = \angle C = 30°$,
∴ $\angle BAC = 180° - 30° - 30° = 120°$。
情况1:当 $\angle APB = 90°$ 时
在 $\triangle APC$ 中,$\angle APC = 180° - 90° = 90°$,
$\angle C = 30°$,
∴ $\angle PAC = x = 180° - 90° - 30° = 60°$。
情况2:当 $\angle BAP = 90°$ 时
∵ $\angle BAC = 120°$,
∴ $\angle PAC = x = \angle BAC - \angle BAP = 120° - 90° = 30°$。
综上,$x$ 的值是 $30$ 或 $60$。
答案:$30$ 或 $60$。
∵ $AB = AC = 3$,
∴ $\triangle ABC$ 是等腰三角形,$\angle B = \angle C = 30°$,
∴ $\angle BAC = 180° - 30° - 30° = 120°$。
情况1:当 $\angle APB = 90°$ 时
在 $\triangle APC$ 中,$\angle APC = 180° - 90° = 90°$,
$\angle C = 30°$,
∴ $\angle PAC = x = 180° - 90° - 30° = 60°$。
情况2:当 $\angle BAP = 90°$ 时
∵ $\angle BAC = 120°$,
∴ $\angle PAC = x = \angle BAC - \angle BAP = 120° - 90° = 30°$。
综上,$x$ 的值是 $30$ 或 $60$。
答案:$30$ 或 $60$。