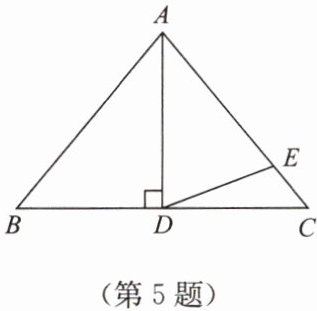
5. 如图,在 $ \triangle ABC $ 中,$ AB = AC $,$ AD \perp BC $,$ \angle BAD = 40^{\circ} $,$ AD = AE $. 求 $ \angle CDE $ 的度数.

答案:解:
∵ AB=AC,AD⊥BC,
∴ ∠CAD=∠BAD=40°,∠ADC=90°.又
∵ AD=AE,
∴ ∠ADE=(180°-40°)/2=70°,
∴ ∠CDE=90°-70°=20°.
∵ AB=AC,AD⊥BC,
∴ ∠CAD=∠BAD=40°,∠ADC=90°.又
∵ AD=AE,
∴ ∠ADE=(180°-40°)/2=70°,
∴ ∠CDE=90°-70°=20°.
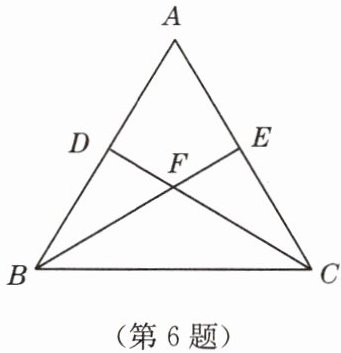
6. 如图,已知在等腰三角形 $ ABC $ 中,$ AB = AC $,点 $ D $,$ E $ 分别在边 $ AB $,$ AC $ 上,且 $ AD = AE $,连接 $ BE $,$ CD $,交于点 $ F $.
(1)判断 $ \angle ABE $ 与 $ \angle ACD $ 的数量关系,并说明理由.
(2)求证:过点 $ A $,$ F $ 的直线垂直平分线段 $ BC $.
(1)判断 $ \angle ABE $ 与 $ \angle ACD $ 的数量关系,并说明理由.
(2)求证:过点 $ A $,$ F $ 的直线垂直平分线段 $ BC $.

答案:
(1) ∠ABE=∠ACD.因为AB=AC,∠BAE=∠CAD,AE=AD,所以△ABE≌△ACD.所以∠ABE=∠ACD.
(2) 因为AB=AC,所以∠ABC=∠ACB.由
(1)可知∠ABE=∠ACD,所以∠FBC=∠FCB,所以FB=FC.又因为AB=AC,所以点A,F均在线段BC的垂直平分线上,即直线AF垂直平分线段BC.
(1) ∠ABE=∠ACD.因为AB=AC,∠BAE=∠CAD,AE=AD,所以△ABE≌△ACD.所以∠ABE=∠ACD.
(2) 因为AB=AC,所以∠ABC=∠ACB.由
(1)可知∠ABE=∠ACD,所以∠FBC=∠FCB,所以FB=FC.又因为AB=AC,所以点A,F均在线段BC的垂直平分线上,即直线AF垂直平分线段BC.
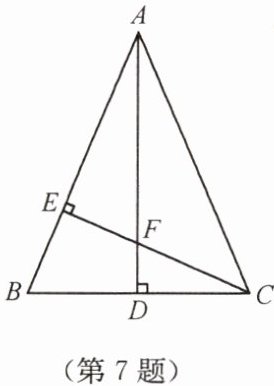
7. 如图,在 $ \triangle ABC $ 中,$ AB = AC $,$ AD \perp BC $,$ CE \perp AB $,$ AE = CE $. 求证:(1)$ \triangle AEF \cong \triangle CEB $;(2)$ AF = 2CD $.

答案:提示:
(1)
∵ AD⊥BC,CE⊥AB,
∴ ∠B+∠BCE=90°.
∴ ∠EAF=∠ECB.由ASA证△AEF≌△CEB.
(2)
∵ △AEF≌△CEB,
∴ AF=BC.
∵ AB=AC,AD⊥BC,
∴ CD=BD,BC=2CD.
∴ AF=2CD.
(1)
∵ AD⊥BC,CE⊥AB,
∴ ∠B+∠BCE=90°.
∴ ∠EAF=∠ECB.由ASA证△AEF≌△CEB.
(2)
∵ △AEF≌△CEB,
∴ AF=BC.
∵ AB=AC,AD⊥BC,
∴ CD=BD,BC=2CD.
∴ AF=2CD.