如图,在 $ \triangle ABC $ 中,$ BA = BC $,$ D $ 在边 $ CB $ 上,且 $ DB = DA = AC $.
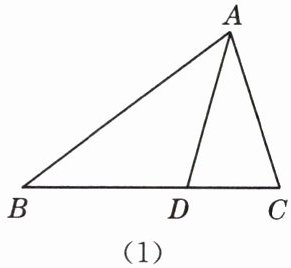
(1)如图(1),$ \angle B = $

(1)如图(1),$ \angle B = $
36
$^{\circ}$,$ \angle C = $72
$^{\circ}$;答案:36;72.
解析:
设$\angle B = x$。
因为$BA = BC$,所以$\angle BAC=\angle C$。
在$\triangle ABC$中,$\angle BAC+\angle C+\angle B=180^{\circ}$,则$\angle C=\frac{180^{\circ}-x}{2}$。
因为$DB = DA$,所以$\angle DAB=\angle B = x$,则$\angle ADC=\angle B+\angle DAB=2x$。
因为$DA = AC$,所以$\angle C=\angle ADC=2x$。
所以$\frac{180^{\circ}-x}{2}=2x$,解得$x = 36^{\circ}$,则$\angle C=2x=72^{\circ}$。
36;72.
因为$BA = BC$,所以$\angle BAC=\angle C$。
在$\triangle ABC$中,$\angle BAC+\angle C+\angle B=180^{\circ}$,则$\angle C=\frac{180^{\circ}-x}{2}$。
因为$DB = DA$,所以$\angle DAB=\angle B = x$,则$\angle ADC=\angle B+\angle DAB=2x$。
因为$DA = AC$,所以$\angle C=\angle ADC=2x$。
所以$\frac{180^{\circ}-x}{2}=2x$,解得$x = 36^{\circ}$,则$\angle C=2x=72^{\circ}$。
36;72.
(2)如图(2),若 $ M $ 为线段 $ BC $ 上的点,过点 $ M $ 作直线 $ MH \perp AD $ 交 $ AD $ 的延长线于点 $ H $,分别交直线 $ AB $,$ AC $ 的延长线于点 $ N $,$ E $.
① 求证:$ \triangle ANE $ 是等腰三角形;
② 试写出线段 $ BN $,$ CE $,$ CD $ 之间的数量关系,并加以证明.
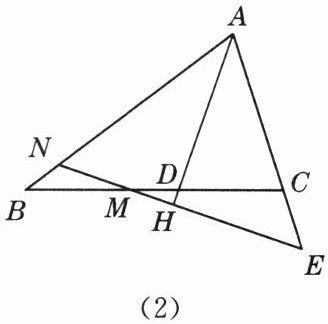
① 求证:$ \triangle ANE $ 是等腰三角形;
② 试写出线段 $ BN $,$ CE $,$ CD $ 之间的数量关系,并加以证明.

答案:① 由
(1)可知∠BAD=∠CAD=36°,且∠AHN=∠AHE=90°,可求得∠ANH=∠AEH=54°,可得AN=AE;
② CD=BN+CE.证明:由①知AN=AE,又
∵ BA=BC,DB=AC,
∴ BN=AB-AN=BC-AE,CE=AE-AC=AE-BD,
∴ BN+CE=BC-BD=CD,即CD=BN+CE.
(1)可知∠BAD=∠CAD=36°,且∠AHN=∠AHE=90°,可求得∠ANH=∠AEH=54°,可得AN=AE;
② CD=BN+CE.证明:由①知AN=AE,又
∵ BA=BC,DB=AC,
∴ BN=AB-AN=BC-AE,CE=AE-AC=AE-BD,
∴ BN+CE=BC-BD=CD,即CD=BN+CE.
1. 等边三角形的三个角都相等,并且每一个角都等于
60
°。答案:60
2. 已知在△ABC中,∠C= 90°,∠A= 30°,BC= 3cm,则AB=
6
cm。答案:6
解析:
在△ABC中,∠C=90°,∠A=30°,BC=3cm。
因为在直角三角形中,30°角所对的直角边等于斜边的一半,∠A=30°,其对边为BC,斜边为AB,所以BC=$\frac{1}{2}$AB。
则AB=2BC=2×3=6cm。
6
因为在直角三角形中,30°角所对的直角边等于斜边的一半,∠A=30°,其对边为BC,斜边为AB,所以BC=$\frac{1}{2}$AB。
则AB=2BC=2×3=6cm。
6
3. 如图,已知直线$l_1//l_2,$将等边三角形如图所示放置,若∠α= 40°,则∠β的度数为
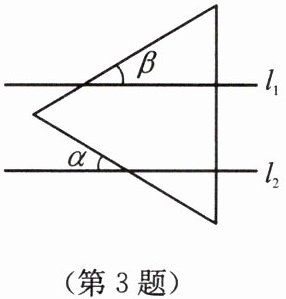
20°
。
答案:20°
解析:
解:过等边三角形的顶点作直线$l_3 // l_1$,
因为$l_1 // l_2$,所以$l_3 // l_2$。
等边三角形内角为$60°$,
由平行线性质得:$\angle \beta = 60° - \angle \alpha$,
已知$\angle \alpha = 40°$,
则$\angle \beta = 60° - 40° = 20°$。
20°
因为$l_1 // l_2$,所以$l_3 // l_2$。
等边三角形内角为$60°$,
由平行线性质得:$\angle \beta = 60° - \angle \alpha$,
已知$\angle \alpha = 40°$,
则$\angle \beta = 60° - 40° = 20°$。
20°
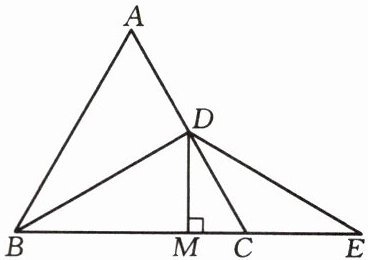
问题 如图,在等边三角形ABC中,点D是AC的中点,点E为BC延长线上一点,且CE= CD,DM⊥BC,垂足是M。求证:点M是BE的中点。
名师指导
由等腰三角形的性质可得∠E= ∠CDE,又由等边三角形的性质可得∠ACB= 60°,∠DBC= 30°,从而易得∠DBE= ∠E,进而可得DB= DE,利用等腰三角形“三线合一”的性质可证得结论。
解题示范(学生在教师指导下,独立完成)
证明:
名师指导
由等腰三角形的性质可得∠E= ∠CDE,又由等边三角形的性质可得∠ACB= 60°,∠DBC= 30°,从而易得∠DBE= ∠E,进而可得DB= DE,利用等腰三角形“三线合一”的性质可证得结论。
解题示范(学生在教师指导下,独立完成)
证明:

答案:证明:
$\because \triangle ABC$是等边三角形,$D$是$AC$的中点,
$\therefore \angle ACB=60°,\angle DBC=\frac{1}{2}\angle ABC = 30°$。
$\because CE = CD$,
$\therefore \angle E=\angle CDE$。
$\because \angle ACB=\angle E+\angle CDE = 60°$,
$\therefore \angle E = 30°$。
$\therefore \angle DBE=\angle E$。
$\therefore DB = DE$。
又$\because DM\perp BE$,
$\therefore M$是$BE$的中点(等腰三角形三线合一)。
$\because \triangle ABC$是等边三角形,$D$是$AC$的中点,
$\therefore \angle ACB=60°,\angle DBC=\frac{1}{2}\angle ABC = 30°$。
$\because CE = CD$,
$\therefore \angle E=\angle CDE$。
$\because \angle ACB=\angle E+\angle CDE = 60°$,
$\therefore \angle E = 30°$。
$\therefore \angle DBE=\angle E$。
$\therefore DB = DE$。
又$\because DM\perp BE$,
$\therefore M$是$BE$的中点(等腰三角形三线合一)。