1. 等边三角形中,两条中线所夹的钝角的度数为(
A.120°
B.130°
C.150°
D.160°
A
)A.120°
B.130°
C.150°
D.160°
答案:A
解析:
设等边三角形为$ \triangle ABC $,中线$ AD $、$ BE $交于点$ O $。
$ \because \triangle ABC $是等边三角形,$ AD $、$ BE $是中线,
$ \therefore AD \perp BC $,$ BE \perp AC $,$ \angle C = 60° $。
在四边形$ CEOD $中,$ \angle ODC = \angle OEC = 90° $,
$ \therefore \angle DOE = 360° - 90° - 90° - 60° = 120° $。
即两条中线所夹钝角为$ 120° $。
A
$ \because \triangle ABC $是等边三角形,$ AD $、$ BE $是中线,
$ \therefore AD \perp BC $,$ BE \perp AC $,$ \angle C = 60° $。
在四边形$ CEOD $中,$ \angle ODC = \angle OEC = 90° $,
$ \therefore \angle DOE = 360° - 90° - 90° - 60° = 120° $。
即两条中线所夹钝角为$ 120° $。
A
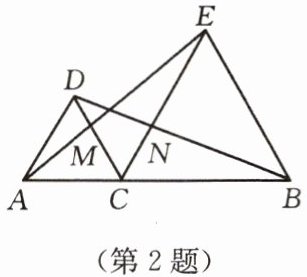
2. 如图,△DAC和△EBC均是等边三角形,AE,BD分别与CD,CE交于点M,N。现有如下结论:(1)△ACE≌△DCB;(2)CM= CN;(3)AC= DN。其中,正确结论的个数是(
A.3个
B.2个
C.1个
D.0个
B
)
A.3个
B.2个
C.1个
D.0个
答案:B
解析:
证明:
(1)
∵△DAC和△EBC均是等边三角形,
∴AC=DC,CE=CB,∠ACD=∠ECB=60°,
∴∠ACD+∠DCE=∠ECB+∠DCE,即∠ACE=∠DCB,
在△ACE和△DCB中,
$\begin{cases}AC=DC \\∠ACE=∠DCB \\CE=CB\end{cases}$
∴△ACE≌△DCB(SAS),结论
(1)正确;
(2) 由
(1)知△ACE≌△DCB,
∴∠CAE=∠CDB,
∵∠ACD=∠ECB=60°,
∴∠DCE=180°-∠ACD-∠ECB=60°,
在△ACM和△DCN中,
$\begin{cases}∠CAM=∠CDN \\AC=DC \\∠ACM=∠DCN=60°\end{cases}$
∴△ACM≌△DCN(ASA),
∴CM=CN,结论
(2)正确;
(3) 由
(2)知△ACM≌△DCN,
∴AM=DN,
在△ACM中,AC>AM(大角对大边,∠AMC>∠ACM=60°),
∴AC>DN,结论
(3)错误;
综上,正确结论的个数是2个,答案选B。
(1)
∵△DAC和△EBC均是等边三角形,
∴AC=DC,CE=CB,∠ACD=∠ECB=60°,
∴∠ACD+∠DCE=∠ECB+∠DCE,即∠ACE=∠DCB,
在△ACE和△DCB中,
$\begin{cases}AC=DC \\∠ACE=∠DCB \\CE=CB\end{cases}$
∴△ACE≌△DCB(SAS),结论
(1)正确;
(2) 由
(1)知△ACE≌△DCB,
∴∠CAE=∠CDB,
∵∠ACD=∠ECB=60°,
∴∠DCE=180°-∠ACD-∠ECB=60°,
在△ACM和△DCN中,
$\begin{cases}∠CAM=∠CDN \\AC=DC \\∠ACM=∠DCN=60°\end{cases}$
∴△ACM≌△DCN(ASA),
∴CM=CN,结论
(2)正确;
(3) 由
(2)知△ACM≌△DCN,
∴AM=DN,
在△ACM中,AC>AM(大角对大边,∠AMC>∠ACM=60°),
∴AC>DN,结论
(3)错误;
综上,正确结论的个数是2个,答案选B。
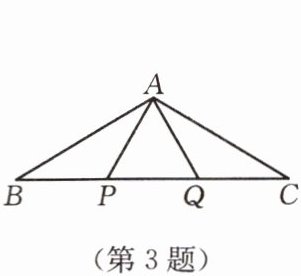
3. 如图,P,Q是△ABC的边BC上的两点,且BP= PQ= QC= AP= AQ,则∠BAC等于
120
°。
答案:120
解析:
证明:
∵ $AP = PQ = AQ$,
∴ $\triangle APQ$ 是等边三角形,
∴ $\angle APQ = \angle AQP = \angle PAQ = 60°$。
∵ $BP = AP$,
∴ $\triangle ABP$ 是等腰三角形,
∴ $\angle B = \angle BAP$。
∵ $\angle APQ$ 是 $\triangle ABP$ 的外角,
∴ $\angle APQ = \angle B + \angle BAP = 2\angle B$,
∴ $\angle B = \frac{1}{2}\angle APQ = 30°$,同理 $\angle C = 30°$。
在 $\triangle ABC$ 中,
$\angle BAC = 180° - \angle B - \angle C = 180° - 30° - 30° = 120°$。
120
∵ $AP = PQ = AQ$,
∴ $\triangle APQ$ 是等边三角形,
∴ $\angle APQ = \angle AQP = \angle PAQ = 60°$。
∵ $BP = AP$,
∴ $\triangle ABP$ 是等腰三角形,
∴ $\angle B = \angle BAP$。
∵ $\angle APQ$ 是 $\triangle ABP$ 的外角,
∴ $\angle APQ = \angle B + \angle BAP = 2\angle B$,
∴ $\angle B = \frac{1}{2}\angle APQ = 30°$,同理 $\angle C = 30°$。
在 $\triangle ABC$ 中,
$\angle BAC = 180° - \angle B - \angle C = 180° - 30° - 30° = 120°$。
120
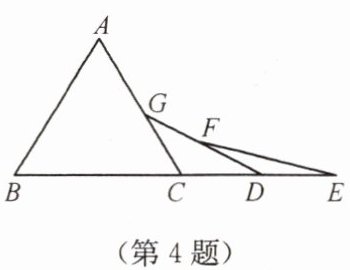
4. 如图,已知△ABC是等边三角形,点B,C,D,E在同一直线上,且CG= CD,DF= DE,则∠E的大小是
15°
。
答案:15°
解析:
证明:
∵△ABC是等边三角形,
∴∠ACB=60°,
∵点B,C,D,E在同一直线上,
∴∠ACD=180°-∠ACB=120°,
∵CG=CD,
∴∠CDG=∠CGD=(180°-∠ACD)/2=(180°-120°)/2=30°,
∵∠CDG是△DEF的外角,
∴∠CDG=∠E+∠DFE,
∵DF=DE,
∴∠E=∠DFE,
∴∠E=∠CDG/2=30°/2=15°。
15°
∵△ABC是等边三角形,
∴∠ACB=60°,
∵点B,C,D,E在同一直线上,
∴∠ACD=180°-∠ACB=120°,
∵CG=CD,
∴∠CDG=∠CGD=(180°-∠ACD)/2=(180°-120°)/2=30°,
∵∠CDG是△DEF的外角,
∴∠CDG=∠E+∠DFE,
∵DF=DE,
∴∠E=∠DFE,
∴∠E=∠CDG/2=30°/2=15°。
15°
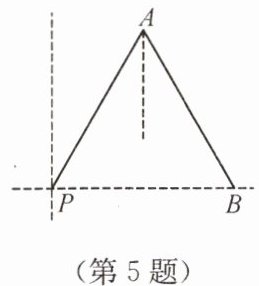
5. 如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔4海里的A处,该海轮沿南偏东30°方向航行
4
海里后,到达位于灯塔P的正东方向的B处。
答案:4
解析:
解:由题意得,∠APN=30°(N为正北方向),AP=4海里,海轮沿南偏东30°方向航行至B处,此时B在P的正东方向。
过A作PQ⊥AB于Q(Q为垂足),则∠PAQ=30°+30°=60°,∠APQ=30°。
在Rt△APQ中,AQ=AP·cos60°=4×$\frac{1}{2}$=2海里,PQ=AP·sin60°=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$海里。
因为B在P的正东方向,所以∠BPQ=90°,∠PBQ=30°。
在Rt△BPQ中,BQ=PQ·cot30°=2$\sqrt{3}$×$\sqrt{3}$=6海里。
AB=BQ - AQ=6 - 2=4海里。
4
过A作PQ⊥AB于Q(Q为垂足),则∠PAQ=30°+30°=60°,∠APQ=30°。
在Rt△APQ中,AQ=AP·cos60°=4×$\frac{1}{2}$=2海里,PQ=AP·sin60°=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$海里。
因为B在P的正东方向,所以∠BPQ=90°,∠PBQ=30°。
在Rt△BPQ中,BQ=PQ·cot30°=2$\sqrt{3}$×$\sqrt{3}$=6海里。
AB=BQ - AQ=6 - 2=4海里。
4
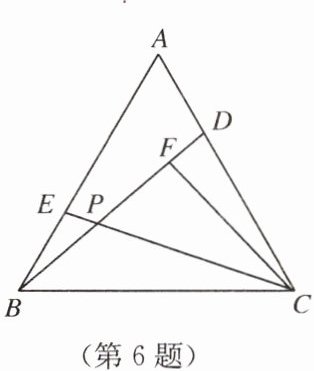
6. 如图,在等边△ABC中,点D,E分别在边AC,AB上,且AD= BE,BD,CE交于点P,CF⊥BD,垂足为F。
(1)求证:BD= CE;
(2)若CP= 7,求PF的长。
(1)求证:BD= CE;
(2)若CP= 7,求PF的长。

答案:
(1)证明:
∵△ABC为等边三角形,
∴AB=BC,∠A=∠ABC=60°.又
∵AD=BE,
∴△ABD≌△BCE(SAS),
∴BD=CE.
(2)PF=3.5.
(1)证明:
∵△ABC为等边三角形,
∴AB=BC,∠A=∠ABC=60°.又
∵AD=BE,
∴△ABD≌△BCE(SAS),
∴BD=CE.
(2)PF=3.5.