2. 下列说法中正确的是(
A.三角形的角平分线是射线
B.过三角形的顶点,且过对边中点的直线是三角形的一条中线
C.三角形的高、中线、角平分线一定在三角形的内部
D.锐角三角形的三条高交于一点
D
)A.三角形的角平分线是射线
B.过三角形的顶点,且过对边中点的直线是三角形的一条中线
C.三角形的高、中线、角平分线一定在三角形的内部
D.锐角三角形的三条高交于一点
答案:D.
3. 如果一个三角形的三条高的交点恰好是这个三角形的一个顶点,那么这个三角形是(
A.锐角三角形
B.直角三角形
C.钝角三角形
D.不能确定
B
)A.锐角三角形
B.直角三角形
C.钝角三角形
D.不能确定
答案:B.
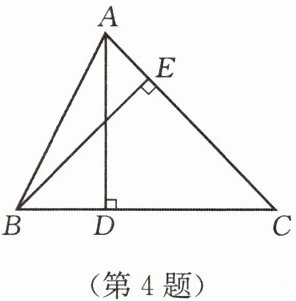
4. 如图,$AD$,$BE$ 分别是 $\triangle ABC$ 的高,$AD = 4\mathrm{cm}$,$BC = 6\mathrm{cm}$,$AC = 5\mathrm{cm}$,则 $BE= $
]
$\frac{24}{5}$cm
.]

答案:$\frac{24}{5}$cm.
解析:
解:$\because AD$是$\triangle ABC$的高,$AD=4\mathrm{cm}$,$BC=6\mathrm{cm}$,
$\therefore S_{\triangle ABC}=\frac{1}{2} × BC × AD=\frac{1}{2} × 6 × 4=12\mathrm{cm^2}$。
$\because BE$是$\triangle ABC$的高,$AC=5\mathrm{cm}$,
$\therefore S_{\triangle ABC}=\frac{1}{2} × AC × BE$,即$12=\frac{1}{2} × 5 × BE$,
解得$BE=\frac{24}{5}\mathrm{cm}$。
$\frac{24}{5}\mathrm{cm}$
$\therefore S_{\triangle ABC}=\frac{1}{2} × BC × AD=\frac{1}{2} × 6 × 4=12\mathrm{cm^2}$。
$\because BE$是$\triangle ABC$的高,$AC=5\mathrm{cm}$,
$\therefore S_{\triangle ABC}=\frac{1}{2} × AC × BE$,即$12=\frac{1}{2} × 5 × BE$,
解得$BE=\frac{24}{5}\mathrm{cm}$。
$\frac{24}{5}\mathrm{cm}$
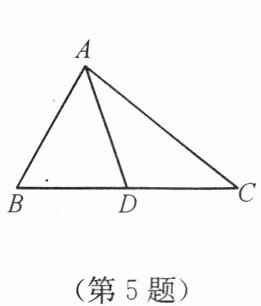
5. 如图,$AD$ 是 $\triangle ABC$ 的边 $BC$ 上的中线,若 $\triangle ABD$ 的周长比 $\triangle ACD$ 的周长小 $5$,则 $AC$ 与 $AB$ 的差为
]
5
.]

答案:5.
解析:
解:
∵AD是△ABC的边BC上的中线,
∴BD=CD。
∵△ABD的周长比△ACD的周长小5,
∴(AC+AD+CD)-(AB+AD+BD)=5。
∵BD=CD,AD=AD,
∴AC-AB=5。
故AC与AB的差为5。
∵AD是△ABC的边BC上的中线,
∴BD=CD。
∵△ABD的周长比△ACD的周长小5,
∴(AC+AD+CD)-(AB+AD+BD)=5。
∵BD=CD,AD=AD,
∴AC-AB=5。
故AC与AB的差为5。
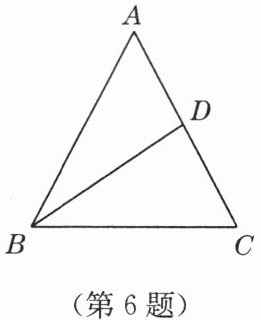
6. 如图,在 $\triangle ABC$ 中,$AB = AC$,$AC$ 边上的中线 $BD$ 把 $\triangle ABC$ 的周长分为 $12\mathrm{cm}$和 $15\mathrm{cm}$ 两个部分,则 $\triangle ABC$ 三边的长分别为
]
8cm,8cm,11cm或10cm,10cm,7cm
.]

答案:8cm,8cm,11cm或10cm,10cm,7cm.
解析:
解:因为 $AB = AC$,设 $AB = AC = 2x\ cm$,则 $AD = DC = x\ cm$。
情况一:$AB + AD = 12\ cm$,$BC + DC = 15\ cm$
$2x + x = 12$,解得 $x = 4$
$AB = AC = 8\ cm$,$BC = 15 - x = 11\ cm$
此时三边长为 $8\ cm, 8\ cm, 11\ cm$,满足三角形三边关系。
情况二:$AB + AD = 15\ cm$,$BC + DC = 12\ cm$
$2x + x = 15$,解得 $x = 5$
$AB = AC = 10\ cm$,$BC = 12 - x = 7\ cm$
此时三边长为 $10\ cm, 10\ cm, 7\ cm$,满足三角形三边关系。
综上,$\triangle ABC$ 三边的长分别为 $8\ cm, 8\ cm, 11\ cm$ 或 $10\ cm, 10\ cm, 7\ cm$。
情况一:$AB + AD = 12\ cm$,$BC + DC = 15\ cm$
$2x + x = 12$,解得 $x = 4$
$AB = AC = 8\ cm$,$BC = 15 - x = 11\ cm$
此时三边长为 $8\ cm, 8\ cm, 11\ cm$,满足三角形三边关系。
情况二:$AB + AD = 15\ cm$,$BC + DC = 12\ cm$
$2x + x = 15$,解得 $x = 5$
$AB = AC = 10\ cm$,$BC = 12 - x = 7\ cm$
此时三边长为 $10\ cm, 10\ cm, 7\ cm$,满足三角形三边关系。
综上,$\triangle ABC$ 三边的长分别为 $8\ cm, 8\ cm, 11\ cm$ 或 $10\ cm, 10\ cm, 7\ cm$。
【问题情境】
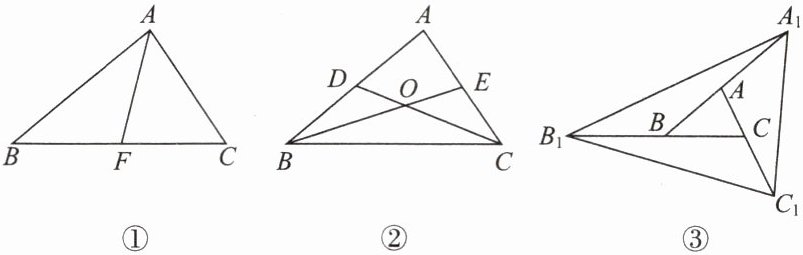
(1) 如图①,在 $\triangle ABC$ 中,$AF$ 为 $BC$ 边上的中线,则 $S_{\triangle ABF}= $______$S_{\triangle ABC}$.
【应用探究】
(2) 如图②,$CD$,$BE$ 是 $\triangle ABC$ 的中线,$S_{\triangle BOC}$ 与 $S_{四边形ADOE}$ 有怎样的数量关系?为什么?
(3) 如图③,点 $A$,$B$,$C$ 分别是线段 $A_1B$,$B_1C$,$C_1A$ 的中点,若 $\triangle ABC$ 的面积是 $1$,求 $\triangle A_1B_1C_1$ 的面积.
]
(1) 如图①,在 $\triangle ABC$ 中,$AF$ 为 $BC$ 边上的中线,则 $S_{\triangle ABF}= $______$S_{\triangle ABC}$.
【应用探究】
(2) 如图②,$CD$,$BE$ 是 $\triangle ABC$ 的中线,$S_{\triangle BOC}$ 与 $S_{四边形ADOE}$ 有怎样的数量关系?为什么?
(3) 如图③,点 $A$,$B$,$C$ 分别是线段 $A_1B$,$B_1C$,$C_1A$ 的中点,若 $\triangle ABC$ 的面积是 $1$,求 $\triangle A_1B_1C_1$ 的面积.
]

答案:
$\frac{1}{2}$.
@@(2) $S_{\triangle BOC}=S_{四边形ADOE}$. 理由如下:∵ CD,BE 是△ABC 的中线,∴ $S_{\triangle BCD}=\frac{1}{2}S_{\triangle ABC}$,$S_{\triangle ABE}=\frac{1}{2}S_{\triangle ABC}$,∴ $S_{\triangle BCD}=S_{\triangle ABE}$,∴ $S_{\triangle BCD}-S_{\triangle BOD}=S_{\triangle ABE}-S_{\triangle BOD}$,即 $S_{\triangle BOC}=S_{四边形ADOE}$. (3) 如图,连接$AB_1,BC_1,A_1C$.∵ 点 C 为$AC_1$的中点,∴ $AC=CC_1$,∴ $S_{\triangle ABC}=S_{\triangle C_1CB}$,∵ 点 B 为$B_1C$的中点,∴ $B_1C=2BC$,∴ $S_{\triangle B_1C_1C}=2S_{\triangle C_1CB}$,∴ $S_{\triangle B_1C_1C}=2S_{\triangle ABC}=2$. 同理可得,$S_{\triangle A_1B_1B}=S_{\triangle A_1AC_1}=2S_{\triangle ABC}=2$,∴ $S_{\triangle A_1B_1C_1}=2+2+2+1=7$.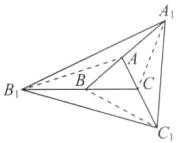
$\frac{1}{2}$.
@@(2) $S_{\triangle BOC}=S_{四边形ADOE}$. 理由如下:∵ CD,BE 是△ABC 的中线,∴ $S_{\triangle BCD}=\frac{1}{2}S_{\triangle ABC}$,$S_{\triangle ABE}=\frac{1}{2}S_{\triangle ABC}$,∴ $S_{\triangle BCD}=S_{\triangle ABE}$,∴ $S_{\triangle BCD}-S_{\triangle BOD}=S_{\triangle ABE}-S_{\triangle BOD}$,即 $S_{\triangle BOC}=S_{四边形ADOE}$. (3) 如图,连接$AB_1,BC_1,A_1C$.∵ 点 C 为$AC_1$的中点,∴ $AC=CC_1$,∴ $S_{\triangle ABC}=S_{\triangle C_1CB}$,∵ 点 B 为$B_1C$的中点,∴ $B_1C=2BC$,∴ $S_{\triangle B_1C_1C}=2S_{\triangle C_1CB}$,∴ $S_{\triangle B_1C_1C}=2S_{\triangle ABC}=2$. 同理可得,$S_{\triangle A_1B_1B}=S_{\triangle A_1AC_1}=2S_{\triangle ABC}=2$,∴ $S_{\triangle A_1B_1C_1}=2+2+2+1=7$.
