1. 在$\triangle ABC$中,若$\angle A = 95^{\circ}$,$\angle B = 40^{\circ}$,则$\angle C$的度数为(
A.$35^{\circ}$
B.$40^{\circ}$
C.$45^{\circ}$
D.$50^{\circ}$
C
)A.$35^{\circ}$
B.$40^{\circ}$
C.$45^{\circ}$
D.$50^{\circ}$
答案:C
解析:
在$\triangle ABC$中,$\angle A + \angle B + \angle C = 180^{\circ}$,已知$\angle A = 95^{\circ}$,$\angle B = 40^{\circ}$,则$\angle C = 180^{\circ} - \angle A - \angle B = 180^{\circ} - 95^{\circ} - 40^{\circ} = 45^{\circ}$。
C
C
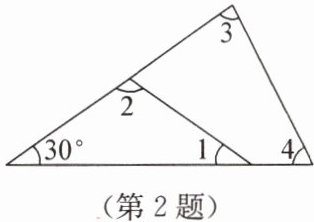
2. 如图,$\angle 1 + \angle 2 + \angle 3 + \angle 4 = $
300
度.
答案:300
解析:
解:在左侧三角形中,$\angle 1 + \angle 2 = 180° - 30° = 150°$。
在右侧三角形中,$\angle 3 + \angle 4 = 180° - 30° = 150°$。
$\angle 1 + \angle 2 + \angle 3 + \angle 4 = 150° + 150° = 300°$。
300
在右侧三角形中,$\angle 3 + \angle 4 = 180° - 30° = 150°$。
$\angle 1 + \angle 2 + \angle 3 + \angle 4 = 150° + 150° = 300°$。
300
3. 在$\triangle ABC$中,$\angle A = \frac{1}{2}\angle B = \frac{1}{3}\angle C$,则$\angle A = $
30°
,$\angle B = $60°
,$\angle C = $90°
.答案:30°,60°,90°
解析:
设$\angle A = x$,则$\angle B = 2x$,$\angle C = 3x$。
因为三角形内角和为$180°$,所以$x + 2x + 3x = 180°$,
$6x = 180°$,
$x = 30°$,
$\angle A = 30°$,$\angle B = 2×30° = 60°$,$\angle C = 3×30° = 90°$。
$30°$,$60°$,$90°$
因为三角形内角和为$180°$,所以$x + 2x + 3x = 180°$,
$6x = 180°$,
$x = 30°$,
$\angle A = 30°$,$\angle B = 2×30° = 60°$,$\angle C = 3×30° = 90°$。
$30°$,$60°$,$90°$
4. 三角形的三个内角之比为$1:3:5$,那么这个三角形的最大内角的度数为
100°
.答案:100°
解析:
设三角形三个内角的度数分别为$x$,$3x$,$5x$。
因为三角形内角和为$180°$,所以$x + 3x + 5x=180°$,
解得$9x=180°$,$x=20°$。
最大内角为$5x=5×20°=100°$。
100°
因为三角形内角和为$180°$,所以$x + 3x + 5x=180°$,
解得$9x=180°$,$x=20°$。
最大内角为$5x=5×20°=100°$。
100°
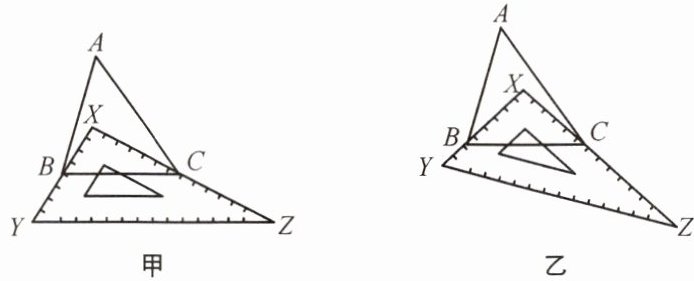
<题目>问题(1)如图甲,有一块直角三角板$XYZ放置在\triangle ABC$上,三角板$XYZ的两条直角边XY$,$XZ恰好分别经过点B$,$C$.在$\triangle ABC$中,若$\angle A = 30^{\circ}$,则$\angle ABC + \angle ACB = $
(2)如图乙,改变直角三角板$XYZ$的位置,使三角板$XYZ的两条直角边XY$,$XZ仍然分别经过点B$,$C$,那么$\angle ABX + \angle ACX$的大小是否变化?若有变化,请举例说明;若无变化,请求出其值.
 名师指导
名师指导
观察图形可知,$\angle ABC + \angle ACB = 180^{\circ} - \angle A$,而$\angle XBC与\angle XCB$互余,从而$(\angle ABX + \angle ACX)等于(\angle ABC + \angle ACB)与(\angle XBC + \angle XCB)$的差.
解题示范(学生在教师指导下,独立完成)
解:
150
度,$\angle XBC + \angle XCB = $90
度.(2)如图乙,改变直角三角板$XYZ$的位置,使三角板$XYZ的两条直角边XY$,$XZ仍然分别经过点B$,$C$,那么$\angle ABX + \angle ACX$的大小是否变化?若有变化,请举例说明;若无变化,请求出其值.
 名师指导
名师指导观察图形可知,$\angle ABC + \angle ACB = 180^{\circ} - \angle A$,而$\angle XBC与\angle XCB$互余,从而$(\angle ABX + \angle ACX)等于(\angle ABC + \angle ACB)与(\angle XBC + \angle XCB)$的差.
解题示范(学生在教师指导下,独立完成)
解:
不变,$60^{\circ}$。
答案:(1)$150$,$90$;(2)不变,$60^{\circ}$。
解析:
(1) 在$\triangle ABC$中,$\angle A = 30^{\circ}$,根据三角形内角和定理,$\angle ABC + \angle ACB = 180^{\circ} - \angle A = 180^{\circ} - 30^{\circ} = 150^{\circ}$。
因为三角板$XYZ$是直角三角板,$\angle X = 90^{\circ}$,在$\triangle XBC$中,$\angle XBC + \angle XCB = 180^{\circ} - \angle X = 180^{\circ} - 90^{\circ} = 90^{\circ}$。
故第一空填$150$,第二空填$90$。
(2) $\angle ABX + \angle ACX$的大小不变。
由(1)知,在$\triangle ABC$中,$\angle ABC + \angle ACB = 180^{\circ} - \angle A$。
在$\triangle XBC$中,$\angle XBC + \angle XCB = 90^{\circ}$。
因为$\angle ABC = \angle ABX + \angle XBC$,$\angle ACB = \angle ACX + \angle XCB$,
所以$\angle ABX + \angle ACX = (\angle ABC + \angle ACB) - (\angle XBC + \angle XCB) = (180^{\circ} - \angle A) - 90^{\circ} = 90^{\circ} - \angle A$。
又因为$\angle A = 30^{\circ}$,所以$\angle ABX + \angle ACX = 90^{\circ} - 30^{\circ} = 60^{\circ}$。
故$\angle ABX + \angle ACX$的值为$60^{\circ}$。
因为三角板$XYZ$是直角三角板,$\angle X = 90^{\circ}$,在$\triangle XBC$中,$\angle XBC + \angle XCB = 180^{\circ} - \angle X = 180^{\circ} - 90^{\circ} = 90^{\circ}$。
故第一空填$150$,第二空填$90$。
(2) $\angle ABX + \angle ACX$的大小不变。
由(1)知,在$\triangle ABC$中,$\angle ABC + \angle ACB = 180^{\circ} - \angle A$。
在$\triangle XBC$中,$\angle XBC + \angle XCB = 90^{\circ}$。
因为$\angle ABC = \angle ABX + \angle XBC$,$\angle ACB = \angle ACX + \angle XCB$,
所以$\angle ABX + \angle ACX = (\angle ABC + \angle ACB) - (\angle XBC + \angle XCB) = (180^{\circ} - \angle A) - 90^{\circ} = 90^{\circ} - \angle A$。
又因为$\angle A = 30^{\circ}$,所以$\angle ABX + \angle ACX = 90^{\circ} - 30^{\circ} = 60^{\circ}$。
故$\angle ABX + \angle ACX$的值为$60^{\circ}$。