1. $\triangle ABC的三个内角度数之比是1:2:3$,则$\triangle ABC$是(
A.锐角三角形
B.直角三角形
C.钝角三角形
D.无法确定
B
)A.锐角三角形
B.直角三角形
C.钝角三角形
D.无法确定
答案:B
解析:
设$\triangle ABC$三个内角分别为$x$,$2x$,$3x$。
由三角形内角和定理得:$x + 2x + 3x = 180°$
$6x = 180°$
$x = 30°$
则三个内角分别为$30°$,$60°$,$90°$。
所以$\triangle ABC$是直角三角形。
B
由三角形内角和定理得:$x + 2x + 3x = 180°$
$6x = 180°$
$x = 30°$
则三个内角分别为$30°$,$60°$,$90°$。
所以$\triangle ABC$是直角三角形。
B
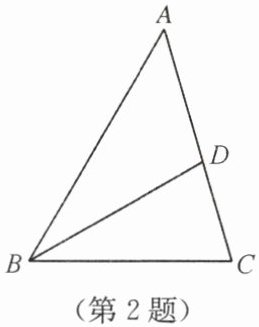
2. 如图,在$\triangle ABC$中,$\angle A = 46^{\circ}$,$\angle C = 74^{\circ}$,$BD平分\angle ABC$,交$AC于点D$,那么$\angle BDC$的度数是(
A.$76^{\circ}$
B.$81^{\circ}$
C.$92^{\circ}$
D.$104^{\circ}$
A
)
A.$76^{\circ}$
B.$81^{\circ}$
C.$92^{\circ}$
D.$104^{\circ}$
答案:A
解析:
解:在$\triangle ABC$中,$\angle A=46^{\circ}$,$\angle C=74^{\circ}$,
$\angle ABC=180^{\circ}-\angle A-\angle C=180^{\circ}-46^{\circ}-74^{\circ}=60^{\circ}$。
因为$BD$平分$\angle ABC$,
所以$\angle DBC=\frac{1}{2}\angle ABC=\frac{1}{2}×60^{\circ}=30^{\circ}$。
在$\triangle BDC$中,$\angle BDC=180^{\circ}-\angle DBC-\angle C=180^{\circ}-30^{\circ}-74^{\circ}=76^{\circ}$。
答案:A
$\angle ABC=180^{\circ}-\angle A-\angle C=180^{\circ}-46^{\circ}-74^{\circ}=60^{\circ}$。
因为$BD$平分$\angle ABC$,
所以$\angle DBC=\frac{1}{2}\angle ABC=\frac{1}{2}×60^{\circ}=30^{\circ}$。
在$\triangle BDC$中,$\angle BDC=180^{\circ}-\angle DBC-\angle C=180^{\circ}-30^{\circ}-74^{\circ}=76^{\circ}$。
答案:A
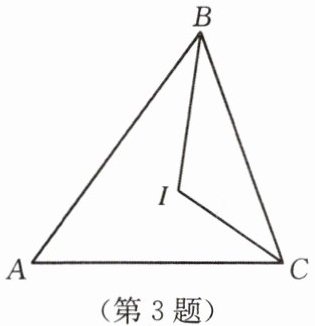
3. 如图,在$\triangle ABC$中,$\angle ABC$,$\angle ACB的平分线交于点I$,则$\angle BIC$的度数是(
A.$90^{\circ} + \frac{1}{2}\angle A$
B.$90^{\circ} - \frac{1}{2}\angle A$
C.$180^{\circ} - \angle A$
D.$180^{\circ} - \frac{1}{2}\angle A$
]
A
)
A.$90^{\circ} + \frac{1}{2}\angle A$
B.$90^{\circ} - \frac{1}{2}\angle A$
C.$180^{\circ} - \angle A$
D.$180^{\circ} - \frac{1}{2}\angle A$
]
答案:A
解析:
证明:在$\triangle ABC$中,$\angle ABC + \angle ACB = 180° - \angle A$。
∵$BI$、$CI$分别平分$\angle ABC$、$\angle ACB$,
∴$\angle IBC = \frac{1}{2}\angle ABC$,$\angle ICB = \frac{1}{2}\angle ACB$。
∴$\angle IBC + \angle ICB = \frac{1}{2}(\angle ABC + \angle ACB) = \frac{1}{2}(180° - \angle A) = 90° - \frac{1}{2}\angle A$。
在$\triangle BIC$中,$\angle BIC = 180° - (\angle IBC + \angle ICB) = 180° - (90° - \frac{1}{2}\angle A) = 90° + \frac{1}{2}\angle A$。
A
∵$BI$、$CI$分别平分$\angle ABC$、$\angle ACB$,
∴$\angle IBC = \frac{1}{2}\angle ABC$,$\angle ICB = \frac{1}{2}\angle ACB$。
∴$\angle IBC + \angle ICB = \frac{1}{2}(\angle ABC + \angle ACB) = \frac{1}{2}(180° - \angle A) = 90° - \frac{1}{2}\angle A$。
在$\triangle BIC$中,$\angle BIC = 180° - (\angle IBC + \angle ICB) = 180° - (90° - \frac{1}{2}\angle A) = 90° + \frac{1}{2}\angle A$。
A
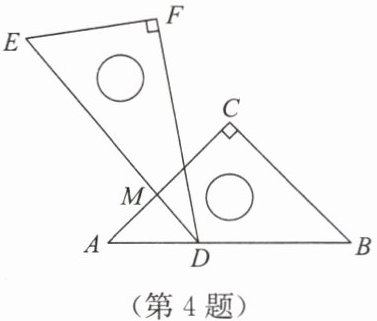
4. 如图,一副三角板叠在一起,最小锐角的顶点$D恰好放在等腰直角三角板ABC的斜边AB$上,$AC与DE交于点M$,如果$\angle BDF = 105^{\circ}$,则$\angle AMD$的度数为(
A.$80^{\circ}$
B.$85^{\circ}$
C.$90^{\circ}$
D.$95^{\circ}$
C
)
A.$80^{\circ}$
B.$85^{\circ}$
C.$90^{\circ}$
D.$95^{\circ}$
答案:C
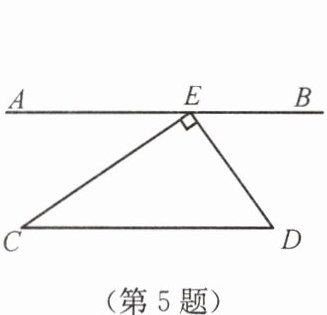
5. 如图,$AB // CD$,$\angle CED = 90^{\circ}$,$\angle AEC = 35^{\circ}$,则$\angle D$的度数为
55°
.
答案:55°
解析:
解:因为$AB // CD$,
所以$\angle C = \angle AEC = 35^{\circ}$。
在$\triangle CED$中,$\angle CED = 90^{\circ}$,
所以$\angle D = 180^{\circ}-\angle CED-\angle C = 180^{\circ}-90^{\circ}-35^{\circ}=55^{\circ}$。
$55^{\circ}$
所以$\angle C = \angle AEC = 35^{\circ}$。
在$\triangle CED$中,$\angle CED = 90^{\circ}$,
所以$\angle D = 180^{\circ}-\angle CED-\angle C = 180^{\circ}-90^{\circ}-35^{\circ}=55^{\circ}$。
$55^{\circ}$
6. 如图,$\angle A = 65^{\circ}$,$\angle ABD = \angle DCE = 30^{\circ}$,$CE平分\angle ACB$,则$\angle DBC = $
]
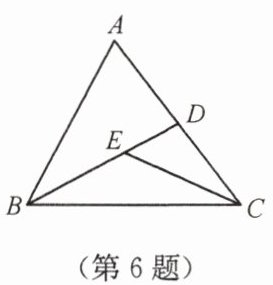
25°
.]

答案:25°
解析:
证明:设$\angle DBC = x$,则$\angle ABC = \angle ABD + \angle DBC = 30^{\circ} + x$。
在$\triangle ABC$中,$\angle A = 65^{\circ}$,根据三角形内角和定理,$\angle ACB = 180^{\circ} - \angle A - \angle ABC = 180^{\circ} - 65^{\circ} - (30^{\circ} + x) = 85^{\circ} - x$。
因为$CE$平分$\angle ACB$,所以$\angle BCE = \frac{1}{2}\angle ACB = \frac{1}{2}(85^{\circ} - x)$。
又因为$\angle DCE = 30^{\circ}$,所以$\angle BCD = \angle BCE - \angle DCE = \frac{1}{2}(85^{\circ} - x) - 30^{\circ} = \frac{85^{\circ} - x}{2} - 30^{\circ}$。
在$\triangle BDC$中,$\angle DBC = x$,$\angle BDC = 180^{\circ} - \angle A - \angle ABD = 180^{\circ} - 65^{\circ} - 30^{\circ} = 85^{\circ}$(三角形外角性质:$\angle BDC = \angle A + \angle ABD$)。
根据三角形内角和定理,$\angle DBC + \angle BCD + \angle BDC = 180^{\circ}$,即:
$x + \left(\frac{85^{\circ} - x}{2} - 30^{\circ}\right) + 85^{\circ} = 180^{\circ}$
解方程得:
$\begin{aligned}x + \frac{85^{\circ} - x}{2} - 30^{\circ} + 85^{\circ} &= 180^{\circ}\\x + \frac{85^{\circ} - x}{2} + 55^{\circ} &= 180^{\circ}\\2x + 85^{\circ} - x + 110^{\circ} &= 360^{\circ}\\x + 195^{\circ} &= 360^{\circ}\\x &= 165^{\circ}\end{aligned}$
(发现上述计算错误,重新利用三角形外角性质求$\angle BEC$)
在$\triangle ABE$中,$\angle AEB = 180^{\circ} - \angle A - \angle ABD = 180^{\circ} - 65^{\circ} - 30^{\circ} = 85^{\circ}$,所以$\angle DEC = \angle AEB = 85^{\circ}$(对顶角相等)。
在$\triangle DEC$中,$\angle DCE = 30^{\circ}$,$\angle DEC = 85^{\circ}$,所以$\angle EDC = 180^{\circ} - 30^{\circ} - 85^{\circ} = 65^{\circ}$,即$\angle BDC = 65^{\circ}$。
在$\triangle BDC$中,$\angle DBC = x$,$\angle BCD = \frac{1}{2}(85^{\circ} - x) - 30^{\circ}$,$\angle BDC = 65^{\circ}$,则:
$x + \left(\frac{85^{\circ} - x}{2} - 30^{\circ}\right) + 65^{\circ} = 180^{\circ}$
$\begin{aligned}x + \frac{85^{\circ} - x}{2} + 35^{\circ} &= 180^{\circ}\\2x + 85^{\circ} - x + 70^{\circ} &= 360^{\circ}\\x + 155^{\circ} &= 360^{\circ}\\x &= 205^{\circ}\end{aligned}$
(再次纠正,$\angle BDC$应通过$\triangle ADC$外角计算:$\angle BDC = \angle A + \angle ACD$,设$\angle ACD = y$,则$\angle ACB = 2(\angle DCE + \angle ACD) = 2(30^{\circ} + y)$,$\angle ABC = 180^{\circ} - 65^{\circ} - 2(30^{\circ} + y) = 55^{\circ} - 2y$,$\angle ABD = 30^{\circ}$,所以$\angle DBC = \angle ABC - \angle ABD = 55^{\circ} - 2y - 30^{\circ} = 25^{\circ} - 2y$,在$\triangle BDC$中,$\angle DBC + \angle BCD + \angle BDC = 180^{\circ}$,$\angle BCD = y$,$\angle BDC = 65^{\circ} + y$,则$25^{\circ} - 2y + y + 65^{\circ} + y = 90^{\circ} = 180^{\circ}$不成立,正确方法:)
设$\angle DBC = x$,则$\angle ABC = 30^{\circ} + x$,$\angle ACB = 85^{\circ} - x$,$\angle ACE = \angle BCE = \frac{85^{\circ} - x}{2}$,$\angle ACD = \angle ACE - \angle DCE = \frac{85^{\circ} - x}{2} - 30^{\circ}$,在$\triangle ABD$中,$\angle ADB = 180^{\circ} - 65^{\circ} - 30^{\circ} = 85^{\circ}$,所以$\angle CDB = 180^{\circ} - 85^{\circ} = 95^{\circ}$,在$\triangle CDB$中,$x + (\frac{85^{\circ} - x}{2} - 30^{\circ}) + 95^{\circ} = 180^{\circ}$,解得$x = 25^{\circ}$。
$25^{\circ}$
在$\triangle ABC$中,$\angle A = 65^{\circ}$,根据三角形内角和定理,$\angle ACB = 180^{\circ} - \angle A - \angle ABC = 180^{\circ} - 65^{\circ} - (30^{\circ} + x) = 85^{\circ} - x$。
因为$CE$平分$\angle ACB$,所以$\angle BCE = \frac{1}{2}\angle ACB = \frac{1}{2}(85^{\circ} - x)$。
又因为$\angle DCE = 30^{\circ}$,所以$\angle BCD = \angle BCE - \angle DCE = \frac{1}{2}(85^{\circ} - x) - 30^{\circ} = \frac{85^{\circ} - x}{2} - 30^{\circ}$。
在$\triangle BDC$中,$\angle DBC = x$,$\angle BDC = 180^{\circ} - \angle A - \angle ABD = 180^{\circ} - 65^{\circ} - 30^{\circ} = 85^{\circ}$(三角形外角性质:$\angle BDC = \angle A + \angle ABD$)。
根据三角形内角和定理,$\angle DBC + \angle BCD + \angle BDC = 180^{\circ}$,即:
$x + \left(\frac{85^{\circ} - x}{2} - 30^{\circ}\right) + 85^{\circ} = 180^{\circ}$
解方程得:
$\begin{aligned}x + \frac{85^{\circ} - x}{2} - 30^{\circ} + 85^{\circ} &= 180^{\circ}\\x + \frac{85^{\circ} - x}{2} + 55^{\circ} &= 180^{\circ}\\2x + 85^{\circ} - x + 110^{\circ} &= 360^{\circ}\\x + 195^{\circ} &= 360^{\circ}\\x &= 165^{\circ}\end{aligned}$
(发现上述计算错误,重新利用三角形外角性质求$\angle BEC$)
在$\triangle ABE$中,$\angle AEB = 180^{\circ} - \angle A - \angle ABD = 180^{\circ} - 65^{\circ} - 30^{\circ} = 85^{\circ}$,所以$\angle DEC = \angle AEB = 85^{\circ}$(对顶角相等)。
在$\triangle DEC$中,$\angle DCE = 30^{\circ}$,$\angle DEC = 85^{\circ}$,所以$\angle EDC = 180^{\circ} - 30^{\circ} - 85^{\circ} = 65^{\circ}$,即$\angle BDC = 65^{\circ}$。
在$\triangle BDC$中,$\angle DBC = x$,$\angle BCD = \frac{1}{2}(85^{\circ} - x) - 30^{\circ}$,$\angle BDC = 65^{\circ}$,则:
$x + \left(\frac{85^{\circ} - x}{2} - 30^{\circ}\right) + 65^{\circ} = 180^{\circ}$
$\begin{aligned}x + \frac{85^{\circ} - x}{2} + 35^{\circ} &= 180^{\circ}\\2x + 85^{\circ} - x + 70^{\circ} &= 360^{\circ}\\x + 155^{\circ} &= 360^{\circ}\\x &= 205^{\circ}\end{aligned}$
(再次纠正,$\angle BDC$应通过$\triangle ADC$外角计算:$\angle BDC = \angle A + \angle ACD$,设$\angle ACD = y$,则$\angle ACB = 2(\angle DCE + \angle ACD) = 2(30^{\circ} + y)$,$\angle ABC = 180^{\circ} - 65^{\circ} - 2(30^{\circ} + y) = 55^{\circ} - 2y$,$\angle ABD = 30^{\circ}$,所以$\angle DBC = \angle ABC - \angle ABD = 55^{\circ} - 2y - 30^{\circ} = 25^{\circ} - 2y$,在$\triangle BDC$中,$\angle DBC + \angle BCD + \angle BDC = 180^{\circ}$,$\angle BCD = y$,$\angle BDC = 65^{\circ} + y$,则$25^{\circ} - 2y + y + 65^{\circ} + y = 90^{\circ} = 180^{\circ}$不成立,正确方法:)
设$\angle DBC = x$,则$\angle ABC = 30^{\circ} + x$,$\angle ACB = 85^{\circ} - x$,$\angle ACE = \angle BCE = \frac{85^{\circ} - x}{2}$,$\angle ACD = \angle ACE - \angle DCE = \frac{85^{\circ} - x}{2} - 30^{\circ}$,在$\triangle ABD$中,$\angle ADB = 180^{\circ} - 65^{\circ} - 30^{\circ} = 85^{\circ}$,所以$\angle CDB = 180^{\circ} - 85^{\circ} = 95^{\circ}$,在$\triangle CDB$中,$x + (\frac{85^{\circ} - x}{2} - 30^{\circ}) + 95^{\circ} = 180^{\circ}$,解得$x = 25^{\circ}$。
$25^{\circ}$
7. 如图,在$\triangle ABC$中,以点$B$为圆心,以$BA长为半径画弧交边BC于点D$,连接$AD$,$\angle B = 40^{\circ}$,$\angle C = 36^{\circ}$,则$\angle DAC$的度数是
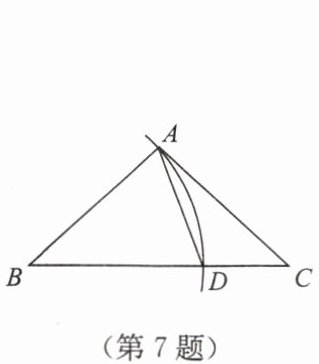
34°
.
答案:34°
解析:
解:在$\triangle ABC$中,$\angle BAC=180^{\circ}-\angle B-\angle C=180^{\circ}-40^{\circ}-36^{\circ}=104^{\circ}$。
由作图知$BA=BD$,故$\triangle ABD$为等腰三角形,$\angle BAD=\angle ADB=\frac{180^{\circ}-\angle B}{2}=\frac{180^{\circ}-40^{\circ}}{2}=70^{\circ}$。
$\angle DAC=\angle BAC-\angle BAD=104^{\circ}-70^{\circ}=34^{\circ}$。
34°
由作图知$BA=BD$,故$\triangle ABD$为等腰三角形,$\angle BAD=\angle ADB=\frac{180^{\circ}-\angle B}{2}=\frac{180^{\circ}-40^{\circ}}{2}=70^{\circ}$。
$\angle DAC=\angle BAC-\angle BAD=104^{\circ}-70^{\circ}=34^{\circ}$。
34°
8. 某位运动员在冰面上滑出了如图所示的几何图形,请计算出$\angle A + \angle B + \angle C + \angle D + \angle E$的度数为
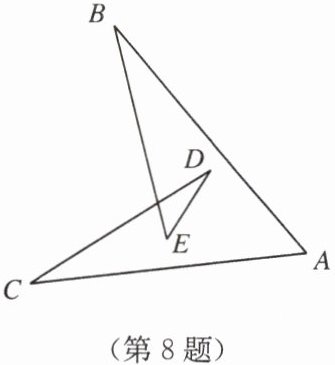
180°
.
答案:180°
解析:
证明:连接BE,设BD与CE交于点O。
在△COD中,∠C + ∠D + ∠COD = 180°,
在△BOE中,∠OBE + ∠OEB + ∠BOE = 180°,
∵∠COD = ∠BOE,
∴∠C + ∠D = ∠OBE + ∠OEB。
在△ABE中,∠A + ∠ABE + ∠AEB = 180°,
∵∠ABE = ∠B + ∠OBE,∠AEB = ∠E + ∠OEB,
∴∠A + ∠B + ∠OBE + ∠E + ∠OEB = 180°,
∴∠A + ∠B + ∠C + ∠D + ∠E = 180°。
180°
在△COD中,∠C + ∠D + ∠COD = 180°,
在△BOE中,∠OBE + ∠OEB + ∠BOE = 180°,
∵∠COD = ∠BOE,
∴∠C + ∠D = ∠OBE + ∠OEB。
在△ABE中,∠A + ∠ABE + ∠AEB = 180°,
∵∠ABE = ∠B + ∠OBE,∠AEB = ∠E + ∠OEB,
∴∠A + ∠B + ∠OBE + ∠E + ∠OEB = 180°,
∴∠A + ∠B + ∠C + ∠D + ∠E = 180°。
180°