9. 如图,在$\triangle ABC$中,$AD是BC$边上的高,$AE是\angle BAC$的平分线.
(1)若$\angle B = 65^{\circ}$,$\angle C = 45^{\circ}$,求$\angle DAE$的度数;
(2)若$\angle B > \angle C$,猜想$\angle B$,$\angle C和\angle DAE$之间有怎样的数量关系,并说明你的理由.
]
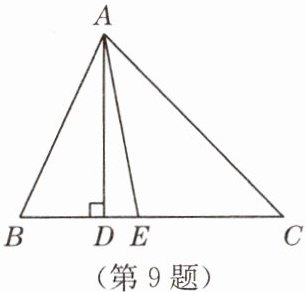
(1)若$\angle B = 65^{\circ}$,$\angle C = 45^{\circ}$,求$\angle DAE$的度数;
(2)若$\angle B > \angle C$,猜想$\angle B$,$\angle C和\angle DAE$之间有怎样的数量关系,并说明你的理由.
]

答案:(1)∠DAE的度数是10°;(2)∠DAE=$\frac{1}{2}$(∠B-∠C). 理由:
∵AD是BC边上的高,
∴∠ADE=90°,
∴∠DAC=90°-∠C.
∵∠BAC+∠B+∠C=180°,
∴∠BAC=180°-∠B-∠C.又
∵AE是∠BAC的平分线,
∴∠EAC=$\frac{1}{2}$∠BAC=$\frac{1}{2}$(180°-∠B-∠C)=90°-$\frac{1}{2}$∠B-$\frac{1}{2}$∠C,
∴∠DAE=∠DAC-∠EAC=90°-∠C-(90°-$\frac{1}{2}$∠B-$\frac{1}{2}$∠C)=$\frac{1}{2}$(∠B-∠C).
∵AD是BC边上的高,
∴∠ADE=90°,
∴∠DAC=90°-∠C.
∵∠BAC+∠B+∠C=180°,
∴∠BAC=180°-∠B-∠C.又
∵AE是∠BAC的平分线,
∴∠EAC=$\frac{1}{2}$∠BAC=$\frac{1}{2}$(180°-∠B-∠C)=90°-$\frac{1}{2}$∠B-$\frac{1}{2}$∠C,
∴∠DAE=∠DAC-∠EAC=90°-∠C-(90°-$\frac{1}{2}$∠B-$\frac{1}{2}$∠C)=$\frac{1}{2}$(∠B-∠C).
当三角形中一个内角是另一个内角的$3$倍时,我们称此三角形为“梦想三角形”.如果一个“梦想三角形”中有一个内角为$108^{\circ}$,求这个“梦想三角形”的最小内角的度数.
答案:36°或18°
解析:
情况一:设$108^{\circ}$内角是另一个内角的$3$倍,
则另一个内角为$108^{\circ}÷3=36^{\circ}$,
第三个内角为$180^{\circ}-108^{\circ}-36^{\circ}=36^{\circ}$,
此时最小内角为$36^{\circ}$;
情况二:设另一个内角是$108^{\circ}$内角的$3$倍,
则另一个内角为$108^{\circ}×3=324^{\circ}$,
因为$324^{\circ}>180^{\circ}$,不符合三角形内角和定理,舍去;
情况三:设除$108^{\circ}$外的两个内角中,一个是另一个的$3$倍,
设较小内角为$x$,则另一个内角为$3x$,
$x+3x+108^{\circ}=180^{\circ}$,
$4x=72^{\circ}$,
$x=18^{\circ}$,
此时最小内角为$18^{\circ}$;
综上,这个“梦想三角形”的最小内角的度数为$36^{\circ}$或$18^{\circ}$。
则另一个内角为$108^{\circ}÷3=36^{\circ}$,
第三个内角为$180^{\circ}-108^{\circ}-36^{\circ}=36^{\circ}$,
此时最小内角为$36^{\circ}$;
情况二:设另一个内角是$108^{\circ}$内角的$3$倍,
则另一个内角为$108^{\circ}×3=324^{\circ}$,
因为$324^{\circ}>180^{\circ}$,不符合三角形内角和定理,舍去;
情况三:设除$108^{\circ}$外的两个内角中,一个是另一个的$3$倍,
设较小内角为$x$,则另一个内角为$3x$,
$x+3x+108^{\circ}=180^{\circ}$,
$4x=72^{\circ}$,
$x=18^{\circ}$,
此时最小内角为$18^{\circ}$;
综上,这个“梦想三角形”的最小内角的度数为$36^{\circ}$或$18^{\circ}$。
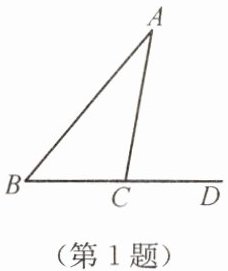
1. 如图,在$\triangle ABC$中,$\angle A = 30^{\circ}$,$\angle B = 50^{\circ}$,延长$BC到D$,则$\angle ACD = $
80
$^{\circ}$。
答案:80
解析:
解:在$\triangle ABC$中,$\angle A=30^{\circ}$,$\angle B=50^{\circ}$,
因为$\angle ACD$是$\triangle ABC$的外角,
所以$\angle ACD=\angle A+\angle B=30^{\circ}+50^{\circ}=80^{\circ}$。
80
因为$\angle ACD$是$\triangle ABC$的外角,
所以$\angle ACD=\angle A+\angle B=30^{\circ}+50^{\circ}=80^{\circ}$。
80
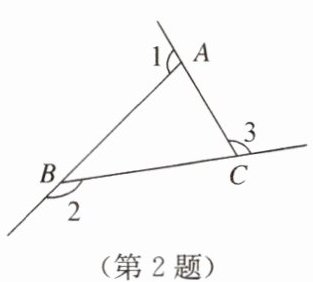
2. 如图,$\angle 1$,$\angle 2$,$\angle 3是\triangle ABC$的三个不同的外角,则$\angle 1 + \angle 2 + \angle 3 = $
360
$^{\circ}$。
答案:360
解析:
解:因为$\angle 1$,$\angle 2$,$\angle 3$是$\triangle ABC$的三个外角,
所以$\angle 1=180^{\circ}-\angle BAC$,$\angle 2=180^{\circ}-\angle ABC$,$\angle 3=180^{\circ}-\angle ACB$。
则$\angle 1+\angle 2+\angle 3=3×180^{\circ}-(\angle BAC+\angle ABC+\angle ACB)$。
又因为三角形内角和为$180^{\circ}$,即$\angle BAC+\angle ABC+\angle ACB=180^{\circ}$,
所以$\angle 1+\angle 2+\angle 3=540^{\circ}-180^{\circ}=360^{\circ}$。
$360$
所以$\angle 1=180^{\circ}-\angle BAC$,$\angle 2=180^{\circ}-\angle ABC$,$\angle 3=180^{\circ}-\angle ACB$。
则$\angle 1+\angle 2+\angle 3=3×180^{\circ}-(\angle BAC+\angle ABC+\angle ACB)$。
又因为三角形内角和为$180^{\circ}$,即$\angle BAC+\angle ABC+\angle ACB=180^{\circ}$,
所以$\angle 1+\angle 2+\angle 3=540^{\circ}-180^{\circ}=360^{\circ}$。
$360$
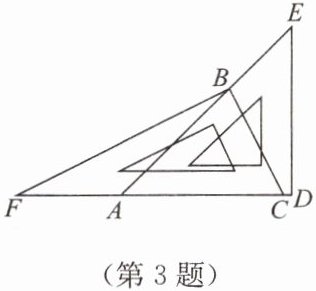
3. 如图,把一副常用的三角板如图所示拼在一起,那么图中$\angle ABF = $
15°
。
答案:15°
解析:
解:由三角板性质可知,$\angle EFD=45°$,$\angle BCF=30°$。
在$\triangle FBC$中,$\angle FBC=180°-\angle EFD-\angle BCF=180°-45°-30°=105°$。
因为$\angle ABC=90°$,所以$\angle ABF=\angle FBC-\angle ABC=105°-90°=15°$。
$15°$
在$\triangle FBC$中,$\angle FBC=180°-\angle EFD-\angle BCF=180°-45°-30°=105°$。
因为$\angle ABC=90°$,所以$\angle ABF=\angle FBC-\angle ABC=105°-90°=15°$。
$15°$
4. 若三角形三个外角的度数比为$2:3:4$,则与之对应的三个内角的度数比为
5:3:1
。答案:5:3:1
解析:
设三角形三个外角的度数分别为$2x$,$3x$,$4x$。
因为三角形外角和为$360°$,所以$2x + 3x + 4x = 360°$,
解得$9x = 360°$,$x = 40°$。
则三个外角分别为$2×40°=80°$,$3×40°=120°$,$4×40°=160°$。
对应的三个内角分别为$180° - 80° = 100°$,$180° - 120° = 60°$,$180° - 160° = 20°$。
三个内角的度数比为$100°:60°:20° = 5:3:1$。
5:3:1
因为三角形外角和为$360°$,所以$2x + 3x + 4x = 360°$,
解得$9x = 360°$,$x = 40°$。
则三个外角分别为$2×40°=80°$,$3×40°=120°$,$4×40°=160°$。
对应的三个内角分别为$180° - 80° = 100°$,$180° - 120° = 60°$,$180° - 160° = 20°$。
三个内角的度数比为$100°:60°:20° = 5:3:1$。
5:3:1