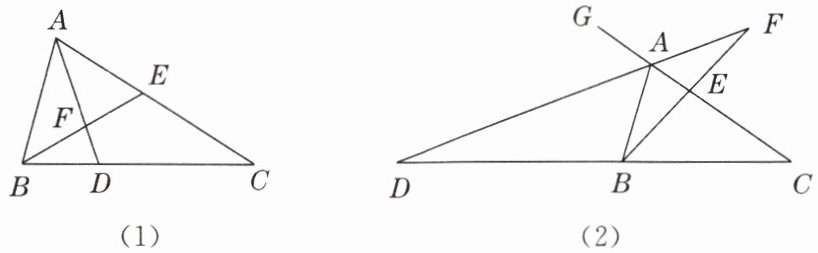
问题 如图,在$\triangle ABC$中,点$E在AC$上,$\angle AEB = \angle ABC$。
(1)图(1)中,作$\angle BAC的角平分线AD$,分别交$CB$,$BE于D$,$F$两点。求证:$\angle EFD = \angle ADC$;
(2)图(2)中,作$\triangle ABC的外角\angle BAG的角平分线AD$所在的直线,分别交$CB$,$BE的延长线于D$,$F$两点,试探究(1)中结论是否仍成立。为什么?
 名师指导
名师指导
(1)首先根据角平分线的性质可得$\angle BAD = \angle DAC$,再根据三角形外角的性质可得$\angle EFD = \angle DAC + \angle AEB$,$\angle ADC = \angle ABC + \angle BAD$,进而得到结论。
(2)类似(1)可得$\angle BAD = \angle DAG$,再根据对顶角相等得$\angle FAE = \angle DAG = \angle BAD$,从而根据外角的性质可得$\angle EFD = \angle AEB - \angle FAE$,$\angle ADC = \angle ABC - \angle BAD$,进而得到结论。
解题示范
(学生在教师指导下,独立完成)
解:
(1)图(1)中,作$\angle BAC的角平分线AD$,分别交$CB$,$BE于D$,$F$两点。求证:$\angle EFD = \angle ADC$;
(2)图(2)中,作$\triangle ABC的外角\angle BAG的角平分线AD$所在的直线,分别交$CB$,$BE的延长线于D$,$F$两点,试探究(1)中结论是否仍成立。为什么?
 名师指导
名师指导(1)首先根据角平分线的性质可得$\angle BAD = \angle DAC$,再根据三角形外角的性质可得$\angle EFD = \angle DAC + \angle AEB$,$\angle ADC = \angle ABC + \angle BAD$,进而得到结论。
(2)类似(1)可得$\angle BAD = \angle DAG$,再根据对顶角相等得$\angle FAE = \angle DAG = \angle BAD$,从而根据外角的性质可得$\angle EFD = \angle AEB - \angle FAE$,$\angle ADC = \angle ABC - \angle BAD$,进而得到结论。
解题示范
(学生在教师指导下,独立完成)
解:
答案:(1)
因为 $AD$ 平分 $\angle BAC$,
所以 $\angle BAD = \angle DAC$,
因为 $\angle EFD = \angle DAC + \angle AEB$,
$\angle ADC = \angle ABC + \angle BAD$,
又因为 $\angle AEB = \angle ABC$,
所以 $\angle EFD = \angle ADC$。
(2)
仍成立,
因为 $AD$ 平分 $\angle BAG$,
所以 $\angle BAD = \angle DAG$,
因为 $\angle FAE = \angle DAG = \angle BAD$,
所以 $\angle EFD = \angle AEB - \angle FAE$,
$\angle ADC = \angle ABC - \angle BAD$,
又因为 $\angle AEB = \angle ABC$,
所以 $\angle EFD = \angle ADC$。
因为 $AD$ 平分 $\angle BAC$,
所以 $\angle BAD = \angle DAC$,
因为 $\angle EFD = \angle DAC + \angle AEB$,
$\angle ADC = \angle ABC + \angle BAD$,
又因为 $\angle AEB = \angle ABC$,
所以 $\angle EFD = \angle ADC$。
(2)
仍成立,
因为 $AD$ 平分 $\angle BAG$,
所以 $\angle BAD = \angle DAG$,
因为 $\angle FAE = \angle DAG = \angle BAD$,
所以 $\angle EFD = \angle AEB - \angle FAE$,
$\angle ADC = \angle ABC - \angle BAD$,
又因为 $\angle AEB = \angle ABC$,
所以 $\angle EFD = \angle ADC$。
1. 下列说法中正确的是(
A.钝角三角形的外角中有两个锐角
B.直角三角形的外角中有三个直角
C.三角形的内角中至少有两个锐角
D.三角形的内角中至少有一个钝角
C
)A.钝角三角形的外角中有两个锐角
B.直角三角形的外角中有三个直角
C.三角形的内角中至少有两个锐角
D.三角形的内角中至少有一个钝角
答案:C
2. 将一副三角尺按如图所示的方式摆放,则$\angle \alpha$的大小为(
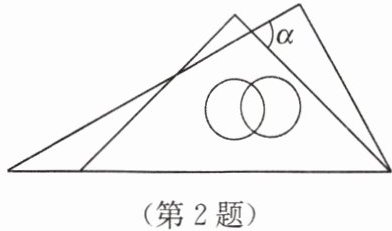
A.$85^{\circ}$
B.$75^{\circ}$
C.$65^{\circ}$
D.$60^{\circ}$
B
)
A.$85^{\circ}$
B.$75^{\circ}$
C.$65^{\circ}$
D.$60^{\circ}$
答案:B