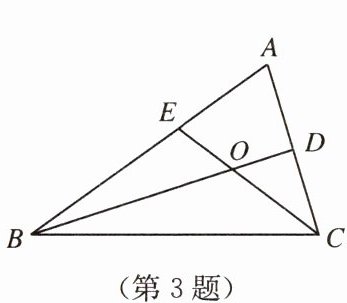
3. 如图,$\triangle ABC的角平分线BD$,$CE相交于点O$,$\angle A = 70^{\circ}$,则$\angle COD$等于(
A.$70^{\circ}$
B.$60^{\circ}$
C.$55^{\circ}$
D.$40^{\circ}$
C
)
A.$70^{\circ}$
B.$60^{\circ}$
C.$55^{\circ}$
D.$40^{\circ}$
答案:C
解析:
证明:在$\triangle ABC$中,$\angle A = 70°$,
$\therefore \angle ABC + \angle ACB = 180° - \angle A = 110°$。
$\because BD$,$CE$是角平分线,
$\therefore \angle OBC = \frac{1}{2}\angle ABC$,$\angle OCB = \frac{1}{2}\angle ACB$,
$\therefore \angle OBC + \angle OCB = \frac{1}{2}(\angle ABC + \angle ACB) = 55°$。
在$\triangle OBC$中,$\angle BOC = 180° - (\angle OBC + \angle OCB) = 125°$,
$\therefore \angle COD = 180° - \angle BOC = 55°$。
C
$\therefore \angle ABC + \angle ACB = 180° - \angle A = 110°$。
$\because BD$,$CE$是角平分线,
$\therefore \angle OBC = \frac{1}{2}\angle ABC$,$\angle OCB = \frac{1}{2}\angle ACB$,
$\therefore \angle OBC + \angle OCB = \frac{1}{2}(\angle ABC + \angle ACB) = 55°$。
在$\triangle OBC$中,$\angle BOC = 180° - (\angle OBC + \angle OCB) = 125°$,
$\therefore \angle COD = 180° - \angle BOC = 55°$。
C
4. 如图,已知$a // b$,$\angle 1 = 50^{\circ}$,$\angle 2 = 115^{\circ}$,则$\angle 3 = $
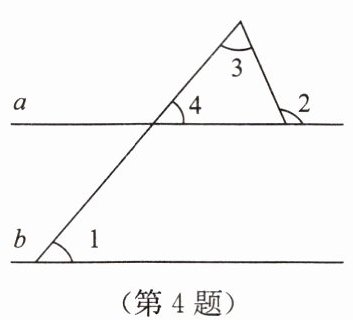
65°
。
答案:65°
5. 如图,在三角形纸片$ABC$中,$\angle A = 65^{\circ}$,$\angle B = 75^{\circ}$。将纸片的一角折叠,使点$C落在\triangle ABC$内,若$\angle 2 = 20^{\circ}$,则$\angle 1 = $
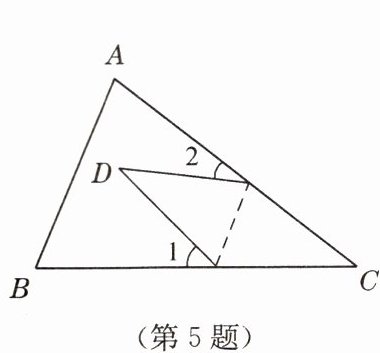
60
$^{\circ}$。
答案:60
解析:
解:在$\triangle ABC$中,$\angle A=65^{\circ}$,$\angle B=75^{\circ}$,
$\angle C=180^{\circ}-\angle A-\angle B=180^{\circ}-65^{\circ}-75^{\circ}=40^{\circ}$。
设折叠后点$C$的对应点为$C'$,则$\angle C'=\angle C=40^{\circ}$,
四边形$ABED$中,$\angle A+\angle B+\angle ADE+\angle BED=360^{\circ}$,
$\triangle DEC'$中,$\angle C'+\angle C'DE+\angle C'ED=180^{\circ}$,
$\angle ADE+\angle C'DE+\angle 1=180^{\circ}$,$\angle BED+\angle C'ED+\angle 2=180^{\circ}$,
$\angle A+\angle B+\angle 1+\angle 2+2\angle C=360^{\circ}$,
$65^{\circ}+75^{\circ}+\angle 1+20^{\circ}+2×40^{\circ}=360^{\circ}$,
解得$\angle 1=60^{\circ}$。
$60$
$\angle C=180^{\circ}-\angle A-\angle B=180^{\circ}-65^{\circ}-75^{\circ}=40^{\circ}$。
设折叠后点$C$的对应点为$C'$,则$\angle C'=\angle C=40^{\circ}$,
四边形$ABED$中,$\angle A+\angle B+\angle ADE+\angle BED=360^{\circ}$,
$\triangle DEC'$中,$\angle C'+\angle C'DE+\angle C'ED=180^{\circ}$,
$\angle ADE+\angle C'DE+\angle 1=180^{\circ}$,$\angle BED+\angle C'ED+\angle 2=180^{\circ}$,
$\angle A+\angle B+\angle 1+\angle 2+2\angle C=360^{\circ}$,
$65^{\circ}+75^{\circ}+\angle 1+20^{\circ}+2×40^{\circ}=360^{\circ}$,
解得$\angle 1=60^{\circ}$。
$60$
6. 如图,分别含有$30^{\circ}和45^{\circ}$角的两个直角三角板,拼成如图所示图形,其中$\angle C = 90^{\circ}$,$\angle B = 45^{\circ}$,$\angle E = 30^{\circ}$,则$\angle BFD$的度数是
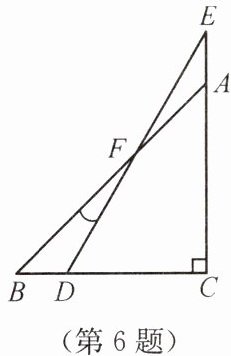
15°
。
答案:15°
解析:
解:设 $ CD = x $,在 $ Rt\triangle ABC $ 中,$ \angle B = 45° $,则 $ AC = BC $,设 $ AC = BC = m $,故 $ BD = BC - CD = m - x $。
在 $ Rt\triangle ECD $ 中,$ \angle E = 30° $,则 $ EC = \sqrt{3}CD = \sqrt{3}x $,$ EA = EC - AC = \sqrt{3}x - m $。
由 $ \triangle AEF \sim \triangle BDF $(对顶角相等,内错角相等),得 $ \frac{EA}{BD} = \frac{AF}{BF} $。
又 $ \angle BAC = 45° $,$ \angle EAC = 90° $,故 $ \angle EAB = 45° $,在 $ \triangle ABF $ 中,$ \angle ABF = 45° $,$ \angle BAF = 45° $,则 $ \angle AFB = 90° $。
在 $ Rt\triangle BDF $ 中,$ \angle BDF = 90° $,$ \angle DBF = 30° $(由三角板角度关系得),故 $ \angle BFD = 60° - 45° = 15° $。
15°
在 $ Rt\triangle ECD $ 中,$ \angle E = 30° $,则 $ EC = \sqrt{3}CD = \sqrt{3}x $,$ EA = EC - AC = \sqrt{3}x - m $。
由 $ \triangle AEF \sim \triangle BDF $(对顶角相等,内错角相等),得 $ \frac{EA}{BD} = \frac{AF}{BF} $。
又 $ \angle BAC = 45° $,$ \angle EAC = 90° $,故 $ \angle EAB = 45° $,在 $ \triangle ABF $ 中,$ \angle ABF = 45° $,$ \angle BAF = 45° $,则 $ \angle AFB = 90° $。
在 $ Rt\triangle BDF $ 中,$ \angle BDF = 90° $,$ \angle DBF = 30° $(由三角板角度关系得),故 $ \angle BFD = 60° - 45° = 15° $。
15°
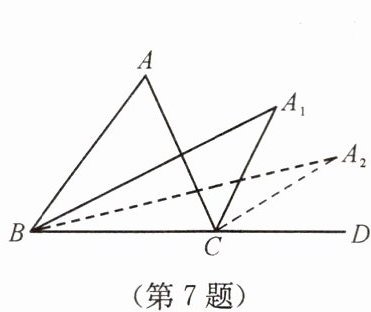
7. 如图,在$\triangle ABC$中,$\angle A = m^{\circ}$,$\angle ABC和\angle ACD的平分线交于点A_1$,得$\angle A_1$;$\angle A_1BC和\angle A_1CD的平分线交于点A_2$,得$\angle A_2$;……;$\angle A_{2024}BC和\angle A_{2024}CD的平分线交于点A_{2025}$,得$\angle A_{2025}$,则$\angle A_{2025} = $
$\frac{m}{2^{2025}}$
度。
答案:$\frac{m}{2^{2025}}$
解析:
证明:
∵$A_1B$平分$\angle ABC$,$A_1C$平分$\angle ACD$,
∴$\angle A_1BC=\frac{1}{2}\angle ABC$,$\angle A_1CD=\frac{1}{2}\angle ACD$。
∵$\angle ACD=\angle A+\angle ABC$,$\angle A_1CD=\angle A_1+\angle A_1BC$,
∴$\frac{1}{2}(\angle A+\angle ABC)=\angle A_1+\frac{1}{2}\angle ABC$,
化简得$\angle A_1=\frac{1}{2}\angle A=\frac{m}{2}$。
同理,$\angle A_2=\frac{1}{2}\angle A_1=\frac{m}{2^2}$,
$\angle A_3=\frac{1}{2}\angle A_2=\frac{m}{2^3}$,
……
依此类推,$\angle A_n=\frac{m}{2^n}$。
当$n=2025$时,$\angle A_{2025}=\frac{m}{2^{2025}}$。
$\frac{m}{2^{2025}}$
∵$A_1B$平分$\angle ABC$,$A_1C$平分$\angle ACD$,
∴$\angle A_1BC=\frac{1}{2}\angle ABC$,$\angle A_1CD=\frac{1}{2}\angle ACD$。
∵$\angle ACD=\angle A+\angle ABC$,$\angle A_1CD=\angle A_1+\angle A_1BC$,
∴$\frac{1}{2}(\angle A+\angle ABC)=\angle A_1+\frac{1}{2}\angle ABC$,
化简得$\angle A_1=\frac{1}{2}\angle A=\frac{m}{2}$。
同理,$\angle A_2=\frac{1}{2}\angle A_1=\frac{m}{2^2}$,
$\angle A_3=\frac{1}{2}\angle A_2=\frac{m}{2^3}$,
……
依此类推,$\angle A_n=\frac{m}{2^n}$。
当$n=2025$时,$\angle A_{2025}=\frac{m}{2^{2025}}$。
$\frac{m}{2^{2025}}$
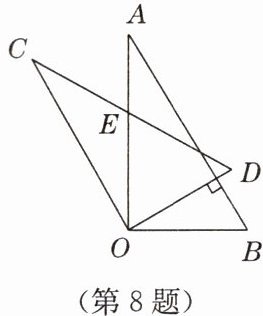
8. 将两块含$30^{\circ}$角的直角三角板叠放成如图所示图形,若$OD \perp AB$,$CD交OA于点E$,则$\angle OED = $
60°
。
答案:60°
解析:
证明:设直角三角板中,$\angle AOB=90^{\circ}$,$\angle OAB=30^{\circ}$,$\angle COD=90^{\circ}$,$\angle OCD=30^{\circ}$。
因为$OD \perp AB$,所以$\angle ODB=90^{\circ}$。
在$Rt\triangle AOB$中,$\angle OAB=30^{\circ}$,则$\angle ABO=60^{\circ}$。
在$Rt\triangle ODB$中,$\angle OBD=60^{\circ}$,所以$\angle DOB=30^{\circ}$。
因为$\angle AOB=90^{\circ}$,所以$\angle AOD=\angle AOB - \angle DOB=60^{\circ}$。
在$\triangle COD$中,$\angle COD=90^{\circ}$,$\angle OCD=30^{\circ}$,则$\angle CDO=60^{\circ}$。
在$\triangle OED$中,$\angle OED=180^{\circ}-\angle AOD-\angle CDO=180^{\circ}-60^{\circ}-60^{\circ}=60^{\circ}$。
$60^{\circ}$
因为$OD \perp AB$,所以$\angle ODB=90^{\circ}$。
在$Rt\triangle AOB$中,$\angle OAB=30^{\circ}$,则$\angle ABO=60^{\circ}$。
在$Rt\triangle ODB$中,$\angle OBD=60^{\circ}$,所以$\angle DOB=30^{\circ}$。
因为$\angle AOB=90^{\circ}$,所以$\angle AOD=\angle AOB - \angle DOB=60^{\circ}$。
在$\triangle COD$中,$\angle COD=90^{\circ}$,$\angle OCD=30^{\circ}$,则$\angle CDO=60^{\circ}$。
在$\triangle OED$中,$\angle OED=180^{\circ}-\angle AOD-\angle CDO=180^{\circ}-60^{\circ}-60^{\circ}=60^{\circ}$。
$60^{\circ}$
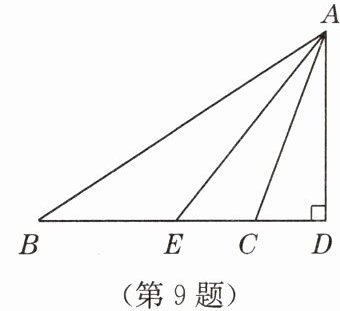
9. 如图,在$\triangle ABC$中,$\angle ACB > 90^{\circ}$,$AE平分\angle BAC$,$AD \perp BC交BC的延长线于点D$。
(1)若$\angle B = 30^{\circ}$,$\angle ACB = 100^{\circ}$,求$\angle EAD$的度数;
(2)若$\angle B = \alpha$,$\angle ACB = \beta$,试用含$\alpha$,$\beta的式子表示\angle EAD$,则$\angle EAD = $
(1)若$\angle B = 30^{\circ}$,$\angle ACB = 100^{\circ}$,求$\angle EAD$的度数;
(2)若$\angle B = \alpha$,$\angle ACB = \beta$,试用含$\alpha$,$\beta的式子表示\angle EAD$,则$\angle EAD = $
$\frac{1}{2}\beta - \frac{1}{2}\alpha$
。(直接写出结论即可)
(1)$\angle EAD=35^{\circ}$
答案:(1)$\angle EAD=35^{\circ}$;(2)$\frac{1}{2}\beta - \frac{1}{2}\alpha$
解析:
(1)在$\triangle ABC$中,$\angle BAC=180^{\circ}-\angle B-\angle ACB=180^{\circ}-30^{\circ}-100^{\circ}=50^{\circ}$。
因为$AE$平分$\angle BAC$,所以$\angle BAE=\frac{1}{2}\angle BAC=25^{\circ}$。
在$\triangle ABD$中,$\angle BAD=90^{\circ}-\angle B=90^{\circ}-30^{\circ}=60^{\circ}$。
所以$\angle EAD=\angle BAD-\angle BAE=60^{\circ}-25^{\circ}=35^{\circ}$。
(2)$\frac{1}{2}\beta - \frac{1}{2}\alpha$