如图,已知$\angle XOY = 90^{\circ}$,点$A$,$B分别在射线OX$,$OY$上移动,$BE是\angle ABY$的平分线,$BE的反向延长线与\angle OAB的平分线相交于点C$。试问随着$A$,$B$的移动,$\angle ACB$的大小是否变化?若不变,请给出证明;若发生变化,请求出变化范围。
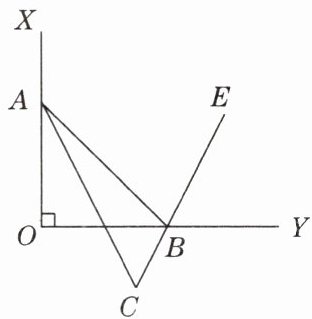

答案:$\angle ACB$的大小不变. 证明:$\because \angle ABY$为$\triangle AOB$的一个外角,$\therefore \angle ABY=90^{\circ}+\angle OAB$. 又$\because BE$为$\angle ABY$的平分线,$\therefore \angle ABE=\frac{1}{2}\angle ABY=\frac{1}{2}(90^{\circ}+\angle OAB)$,$\therefore \angle ABE=45^{\circ}+\frac{1}{2}\angle OAB$. $\because AC$是$\angle OAB$的平分线,$\therefore \angle BAC=\frac{1}{2}\angle OAB$. $\because \angle ABE=\angle C+\angle CAB$,$\therefore \angle C=\angle ABE-\angle CAB=45^{\circ}+\frac{1}{2}\angle OAB-\frac{1}{2}\angle OAB=45^{\circ}$,即$\angle ACB$的大小不变.
1.
三角形三条中线的交点
叫作三角形的重心.答案:三角形三条中线的交点.
2. 在如图所示的网格中,每个小正方形的边长均为1,△ABC的顶点均在格点上,则△ABC的重心在(
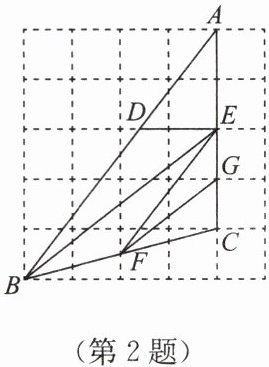
A.线段DE上
B.线段EF上
C.线段BE上
D.线段FG上
C
)
A.线段DE上
B.线段EF上
C.线段BE上
D.线段FG上
答案:C
解析:
以点B为坐标原点,建立平面直角坐标系。
由图可知,点A(2,4),点B(0,0),点C(3,1)。
三角形重心坐标公式:$(\frac{x_A+x_B+x_C}{3},\frac{y_A+y_B+y_C}{3})$。
计算得:$x=\frac{2+0+3}{3}=\frac{5}{3}$,$y=\frac{4+0+1}{3}=\frac{5}{3}$。
线段BE上点的横坐标为2,纵坐标范围符合$\frac{5}{3}$,故重心在BE上。
C
由图可知,点A(2,4),点B(0,0),点C(3,1)。
三角形重心坐标公式:$(\frac{x_A+x_B+x_C}{3},\frac{y_A+y_B+y_C}{3})$。
计算得:$x=\frac{2+0+3}{3}=\frac{5}{3}$,$y=\frac{4+0+1}{3}=\frac{5}{3}$。
线段BE上点的横坐标为2,纵坐标范围符合$\frac{5}{3}$,故重心在BE上。
C
问题 如图,点O为△ABC的重心,连接BO并延长交AC于点D,连接CO并延长交AB于点E,求S₍△OCD₎:S₍四边形AEOD₎的值.
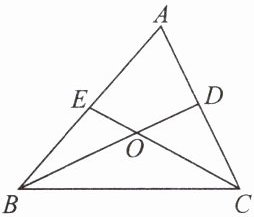
名师指导
本题关键是利用三角形重心的概念,以及同底(等底)或同高(等高)的两三角形面积之间的关系. 连接OA,根据重心的概念得出S₍△AOD₎= S₍△OCD₎= S₍△EOB₎= S₍△AOE₎,设S₍△OCD₎= x,接下来通过面积的和差和等量代换即可得出答案.
解题示范(学生在教师指导下,独立完成)
解:

名师指导
本题关键是利用三角形重心的概念,以及同底(等底)或同高(等高)的两三角形面积之间的关系. 连接OA,根据重心的概念得出S₍△AOD₎= S₍△OCD₎= S₍△EOB₎= S₍△AOE₎,设S₍△OCD₎= x,接下来通过面积的和差和等量代换即可得出答案.
解题示范(学生在教师指导下,独立完成)
解:
答案:1:2
解析:
连接OA。
∵点O为△ABC的重心,∴BD、CE为△ABC的中线,D、E分别为AC、AB中点,且BO:OD=2:1,CO:OE=2:1。
∵D为AC中点,∴AD=DC。△AOD与△OCD等底(AD=DC)同高,∴S△AOD=S△OCD。设S△OCD=x,则S△AOD=x。
∵CO:OE=2:1,△AOC与△AOE同高,∴S△AOC:S△AOE=CO:OE=2:1。又S△AOC=S△AOD+S△OCD=x+x=2x,∴S△AOE=x。
四边形AEOD的面积=S△AOE+S△AOD=x+x=2x。
故S△OCD:S四边形AEOD=x:2x=1:2。
∵点O为△ABC的重心,∴BD、CE为△ABC的中线,D、E分别为AC、AB中点,且BO:OD=2:1,CO:OE=2:1。
∵D为AC中点,∴AD=DC。△AOD与△OCD等底(AD=DC)同高,∴S△AOD=S△OCD。设S△OCD=x,则S△AOD=x。
∵CO:OE=2:1,△AOC与△AOE同高,∴S△AOC:S△AOE=CO:OE=2:1。又S△AOC=S△AOD+S△OCD=x+x=2x,∴S△AOE=x。
四边形AEOD的面积=S△AOE+S△AOD=x+x=2x。
故S△OCD:S四边形AEOD=x:2x=1:2。