1. 三角形的重心是三角形的(
A.三条角平分线的交点
B.一条边的中线与另一条边的高的交点
C.三条高的交点
D.三条中线的交点
D
)A.三条角平分线的交点
B.一条边的中线与另一条边的高的交点
C.三条高的交点
D.三条中线的交点
答案:D
2. 如图,点O是△ABC的重心,连接AO并延长交BC于点D. 连接BO并延长交AC于点E,则下列说法一定正确的是(
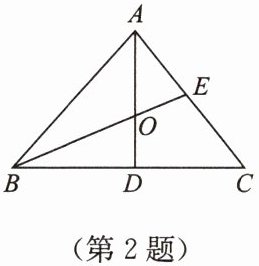
A.AD是△ABC的高
B.BO是△ABD的中线
C.AO是△ABE的角平分线
D.△AOE与△BOD的面积相等
D
)
A.AD是△ABC的高
B.BO是△ABD的中线
C.AO是△ABE的角平分线
D.△AOE与△BOD的面积相等
答案:D
解析:
证明:
∵点O是△ABC的重心,
∴AD、BE是△ABC的中线,即D为BC中点,E为AC中点,
∴BD=DC,AE=EC。
设S△ABC=12k(k>0),则S△ABD=S△ADC=6k,S△ABE=S△CBE=6k。
∵重心O分中线所得比为AO:OD=2:1,BO:OE=2:1,
∴S△AOE=1/3 S△ABE=1/3×6k=2k,
S△BOD=1/3 S△ABD=1/3×6k=2k。
∴S△AOE=S△BOD。
D
∵点O是△ABC的重心,
∴AD、BE是△ABC的中线,即D为BC中点,E为AC中点,
∴BD=DC,AE=EC。
设S△ABC=12k(k>0),则S△ABD=S△ADC=6k,S△ABE=S△CBE=6k。
∵重心O分中线所得比为AO:OD=2:1,BO:OE=2:1,
∴S△AOE=1/3 S△ABE=1/3×6k=2k,
S△BOD=1/3 S△ABD=1/3×6k=2k。
∴S△AOE=S△BOD。
D
3. 如图所示的网格由边长相等的小正方形组成,点A,B,C,D,E,F,G在小正方形的格点上,则△ABC的重心是(
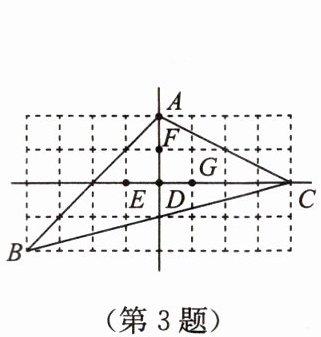
A.点D
B.点E
C.点F
D.点G
A
)
A.点D
B.点E
C.点F
D.点G
答案:A
解析:
解:三角形重心是三条中线的交点。
连接$A$与$BC$中点,$B$与$AC$中点,两中线交于点$D$。
答案:A
连接$A$与$BC$中点,$B$与$AC$中点,两中线交于点$D$。
答案:A
4. 如图,点G是△ABC的重心,若$S₍△BGC₎= 6 cm^2,$则S₍△ABC₎=
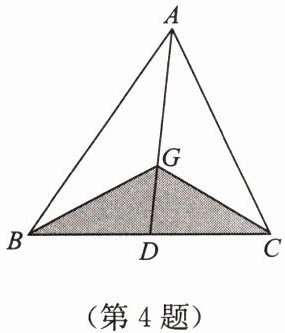
18
$cm^2.$
答案:18
解析:
证明:连接AD,
∵点G是△ABC的重心,
∴AD是△ABC的中线,且AG=2GD,
∴S△ABD=S△ACD=$\frac{1}{2}$S△ABC,
∵S△BGD=S△CGD=$\frac{1}{2}$S△BGC=3 cm2,
又
∵AG=2GD,
∴S△ABG=2S△BGD=6 cm2,S△AGC=2S△CGD=6 cm2,
∴S△ABC=S△ABG+S△AGC+S△BGC=6+6+6=18 cm2.
18
∵点G是△ABC的重心,
∴AD是△ABC的中线,且AG=2GD,
∴S△ABD=S△ACD=$\frac{1}{2}$S△ABC,
∵S△BGD=S△CGD=$\frac{1}{2}$S△BGC=3 cm2,
又
∵AG=2GD,
∴S△ABG=2S△BGD=6 cm2,S△AGC=2S△CGD=6 cm2,
∴S△ABC=S△ABG+S△AGC+S△BGC=6+6+6=18 cm2.
18
5. 如图,△ABC的顶点在正方形网格的格点上,每个小正方形的边长为1,请按要求画图并回答问题:
(1)请画图找出△ABC的重心点P;
(2)连接PA,PC,直接写出△PAC的面积.
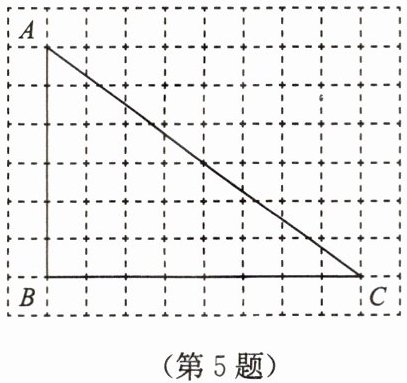
(1)请画图找出△ABC的重心点P;
(2)连接PA,PC,直接写出△PAC的面积.

答案:
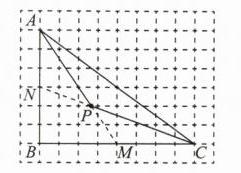
(1) 如图所示,点P即为所求.
(2) 由图可得$S_{\triangle APC}=S_{\triangle AMC}-S_{\triangle PMC}=\frac{1}{2}×6×4-\frac{1}{2}×4×2=8$.

(1) 如图所示,点P即为所求.
(2) 由图可得$S_{\triangle APC}=S_{\triangle AMC}-S_{\triangle PMC}=\frac{1}{2}×6×4-\frac{1}{2}×4×2=8$.