【操作发现】三角形三个顶点与重心的连线段,将该三角形面积三等分.
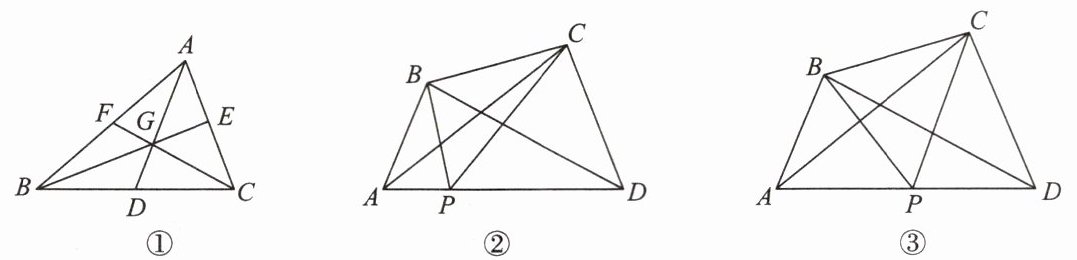
(1)如图①,在△ABC中,中线AD,BE,CF相交于点G. 求证:S₍△ABG₎= 1/3 S₍△ABC₎.
【提出问题】如图②,探究在四边形ABCD中,P是AD边上任意一点,△PBC与△ABC和△DBC的面积之间的关系.
(2)为了解决这个问题,我们可以先从一些简单的、特殊的情形入手:如图③,当AP= 1/2 AD时,探求S₍△PBC₎与S₍△ABC₎和S₍△DBC₎之间的关系,写出求解过程.
【问题解决】
(3)推广,当AP= 1/n AD(n表示正整数)时,直接写出S₍△PBC₎与S₍△ABC₎和S₍△DBC₎之间的关系:
(4)一般地,当AP= m/n AD(0≤m/n ≤1)时,直接写出S₍△PBC₎与S₍△ABC₎和S₍△DBC₎之间的关系:
(1)
(2)
(1)如图①,在△ABC中,中线AD,BE,CF相交于点G. 求证:S₍△ABG₎= 1/3 S₍△ABC₎.
【提出问题】如图②,探究在四边形ABCD中,P是AD边上任意一点,△PBC与△ABC和△DBC的面积之间的关系.
(2)为了解决这个问题,我们可以先从一些简单的、特殊的情形入手:如图③,当AP= 1/2 AD时,探求S₍△PBC₎与S₍△ABC₎和S₍△DBC₎之间的关系,写出求解过程.

【问题解决】
(3)推广,当AP= 1/n AD(n表示正整数)时,直接写出S₍△PBC₎与S₍△ABC₎和S₍△DBC₎之间的关系:
$S_{\triangle PBC}=\frac{1}{n}S_{\triangle DBC}+\frac{n - 1}{n}S_{\triangle ABC}$
.(4)一般地,当AP= m/n AD(0≤m/n ≤1)时,直接写出S₍△PBC₎与S₍△ABC₎和S₍△DBC₎之间的关系:
$S_{\triangle PBC}=\frac{m}{n}S_{\triangle DBC}+\frac{n - m}{n}S_{\triangle ABC}$
.(1)
如题图①,$\because BD=CD$,$\therefore S_{\triangle ABD}=\frac{1}{2}S_{\triangle ABC}$. $\because G$是重心,$\therefore AG=2DG$,$\therefore S_{\triangle ABG}=\frac{2}{3}S_{\triangle ABD}=\frac{1}{3}S_{\triangle ABC}$.
(2)
结论:$S_{\triangle PBC}=\frac{1}{2}S_{\triangle DBC}+\frac{1}{2}S_{\triangle ABC}$. 理由:如题图③,$\because AP=\frac{1}{2}AD$,$\triangle ABP$和$\triangle ABD$的高相等,$\therefore S_{\triangle ABP}=\frac{1}{2}S_{\triangle ABD}$. $\because PD=\frac{1}{2}AD$,$\triangle CDP$和$\triangle CDA$的高相等,$\therefore S_{\triangle CDP}=\frac{1}{2}S_{\triangle CDA}$. $\therefore S_{\triangle PBC}=S_{四边形ABCD}-S_{\triangle ABP}-S_{\triangle CDP}=S_{四边形ABCD}-\frac{1}{2}S_{\triangle ABD}-\frac{1}{2}S_{\triangle CDA}=S_{四边形ABCD}-\frac{1}{2}(S_{四边形ABCD}-S_{\triangle DBC})-\frac{1}{2}(S_{四边形ABCD}-S_{\triangle ABC})=\frac{1}{2}S_{\triangle DBC}+\frac{1}{2}S_{\triangle ABC}$.
答案:
(1) 如题图①,$\because BD=CD$,$\therefore S_{\triangle ABD}=\frac{1}{2}S_{\triangle ABC}$. $\because G$是重心,$\therefore AG=2DG$,$\therefore S_{\triangle ABG}=\frac{2}{3}S_{\triangle ABD}=\frac{1}{3}S_{\triangle ABC}$.
(2) 结论:$S_{\triangle PBC}=\frac{1}{2}S_{\triangle DBC}+\frac{1}{2}S_{\triangle ABC}$. 理由:如题图③,$\because AP=\frac{1}{2}AD$,$\triangle ABP$和$\triangle ABD$的高相等,$\therefore S_{\triangle ABP}=\frac{1}{2}S_{\triangle ABD}$. $\because PD=\frac{1}{2}AD$,$\triangle CDP$和$\triangle CDA$的高相等,$\therefore S_{\triangle CDP}=\frac{1}{2}S_{\triangle CDA}$. $\therefore S_{\triangle PBC}=S_{四边形ABCD}-S_{\triangle ABP}-S_{\triangle CDP}=S_{四边形ABCD}-\frac{1}{2}S_{\triangle ABD}-\frac{1}{2}S_{\triangle CDA}=S_{四边形ABCD}-\frac{1}{2}(S_{四边形ABCD}-S_{\triangle DBC})-\frac{1}{2}(S_{四边形ABCD}-S_{\triangle ABC})=\frac{1}{2}S_{\triangle DBC}+\frac{1}{2}S_{\triangle ABC}$.
(3) 结论:$S_{\triangle PBC}=\frac{1}{n}S_{\triangle DBC}+\frac{n - 1}{n}S_{\triangle ABC}$. 理由:$\because AP=\frac{1}{n}AD$,$\triangle ABP$和$\triangle ABD$的高相等,$\therefore S_{\triangle ABP}=\frac{1}{n}S_{\triangle ABD}$. 又$\because PD=\frac{n - 1}{n}AD$,$\triangle CDP$和$\triangle CDA$的高相等,$\therefore S_{\triangle CDP}=\frac{n - 1}{n}S_{\triangle CDA}$,$\therefore S_{\triangle PBC}=S_{四边形ABCD}-S_{\triangle ABP}-S_{\triangle CDP}=S_{四边形ABCD}-\frac{1}{n}S_{\triangle ABD}-\frac{n - 1}{n}S_{\triangle CDA}=S_{四边形ABCD}-\frac{1}{n}(S_{四边形ABCD}-S_{\triangle DBC})-\frac{n - 1}{n}(S_{四边形ABCD}-S_{\triangle ABC})=\frac{1}{n}S_{\triangle DBC}+\frac{n - 1}{n}S_{\triangle ABC}$.
(4) 结论:$S_{\triangle PBC}=\frac{m}{n}S_{\triangle DBC}+\frac{n - m}{n}S_{\triangle ABC}$. 理由:$\because AP=\frac{m}{n}AD$,$\triangle ABP$和$\triangle ABD$的高相等,$\therefore S_{\triangle ABP}=\frac{m}{n}S_{\triangle ABD}$. 又$\because PD=\frac{n - m}{n}AD$,$\triangle CDP$和$\triangle CDA$的高相等,$\therefore S_{\triangle CDP}=\frac{n - m}{n}S_{\triangle CDA}$,$\therefore S_{\triangle PBC}=S_{四边形ABCD}-S_{\triangle ABP}-S_{\triangle CDP}=S_{四边形ABCD}-\frac{m}{n}S_{\triangle ABD}-\frac{n - m}{n}S_{\triangle CDA}=S_{四边形ABCD}-\frac{m}{n}(S_{四边形ABCD}-S_{\triangle DBC})-\frac{n - m}{n}(S_{四边形ABCD}-S_{\triangle ABC})=\frac{m}{n}S_{\triangle DBC}+\frac{n - m}{n}S_{\triangle ABC}$.
(1) 如题图①,$\because BD=CD$,$\therefore S_{\triangle ABD}=\frac{1}{2}S_{\triangle ABC}$. $\because G$是重心,$\therefore AG=2DG$,$\therefore S_{\triangle ABG}=\frac{2}{3}S_{\triangle ABD}=\frac{1}{3}S_{\triangle ABC}$.
(2) 结论:$S_{\triangle PBC}=\frac{1}{2}S_{\triangle DBC}+\frac{1}{2}S_{\triangle ABC}$. 理由:如题图③,$\because AP=\frac{1}{2}AD$,$\triangle ABP$和$\triangle ABD$的高相等,$\therefore S_{\triangle ABP}=\frac{1}{2}S_{\triangle ABD}$. $\because PD=\frac{1}{2}AD$,$\triangle CDP$和$\triangle CDA$的高相等,$\therefore S_{\triangle CDP}=\frac{1}{2}S_{\triangle CDA}$. $\therefore S_{\triangle PBC}=S_{四边形ABCD}-S_{\triangle ABP}-S_{\triangle CDP}=S_{四边形ABCD}-\frac{1}{2}S_{\triangle ABD}-\frac{1}{2}S_{\triangle CDA}=S_{四边形ABCD}-\frac{1}{2}(S_{四边形ABCD}-S_{\triangle DBC})-\frac{1}{2}(S_{四边形ABCD}-S_{\triangle ABC})=\frac{1}{2}S_{\triangle DBC}+\frac{1}{2}S_{\triangle ABC}$.
(3) 结论:$S_{\triangle PBC}=\frac{1}{n}S_{\triangle DBC}+\frac{n - 1}{n}S_{\triangle ABC}$. 理由:$\because AP=\frac{1}{n}AD$,$\triangle ABP$和$\triangle ABD$的高相等,$\therefore S_{\triangle ABP}=\frac{1}{n}S_{\triangle ABD}$. 又$\because PD=\frac{n - 1}{n}AD$,$\triangle CDP$和$\triangle CDA$的高相等,$\therefore S_{\triangle CDP}=\frac{n - 1}{n}S_{\triangle CDA}$,$\therefore S_{\triangle PBC}=S_{四边形ABCD}-S_{\triangle ABP}-S_{\triangle CDP}=S_{四边形ABCD}-\frac{1}{n}S_{\triangle ABD}-\frac{n - 1}{n}S_{\triangle CDA}=S_{四边形ABCD}-\frac{1}{n}(S_{四边形ABCD}-S_{\triangle DBC})-\frac{n - 1}{n}(S_{四边形ABCD}-S_{\triangle ABC})=\frac{1}{n}S_{\triangle DBC}+\frac{n - 1}{n}S_{\triangle ABC}$.
(4) 结论:$S_{\triangle PBC}=\frac{m}{n}S_{\triangle DBC}+\frac{n - m}{n}S_{\triangle ABC}$. 理由:$\because AP=\frac{m}{n}AD$,$\triangle ABP$和$\triangle ABD$的高相等,$\therefore S_{\triangle ABP}=\frac{m}{n}S_{\triangle ABD}$. 又$\because PD=\frac{n - m}{n}AD$,$\triangle CDP$和$\triangle CDA$的高相等,$\therefore S_{\triangle CDP}=\frac{n - m}{n}S_{\triangle CDA}$,$\therefore S_{\triangle PBC}=S_{四边形ABCD}-S_{\triangle ABP}-S_{\triangle CDP}=S_{四边形ABCD}-\frac{m}{n}S_{\triangle ABD}-\frac{n - m}{n}S_{\triangle CDA}=S_{四边形ABCD}-\frac{m}{n}(S_{四边形ABCD}-S_{\triangle DBC})-\frac{n - m}{n}(S_{四边形ABCD}-S_{\triangle ABC})=\frac{m}{n}S_{\triangle DBC}+\frac{n - m}{n}S_{\triangle ABC}$.