1. 现有长度分别为 $2\mathrm{cm}$,$3\mathrm{cm}$,$4\mathrm{cm}$,$5\mathrm{cm}$ 的木棒,从中任取三根,能组成三角形的个数为(
A.$1$
B.$2$
C.$3$
D.$4$
C
)A.$1$
B.$2$
C.$3$
D.$4$
答案:C
解析:
从四根木棒中任取三根,所有可能的组合为:
1. $2\mathrm{cm},3\mathrm{cm},4\mathrm{cm}$:$2 + 3 > 4$,$2 + 4 > 3$,$3 + 4 > 2$,能组成三角形;
2. $2\mathrm{cm},3\mathrm{cm},5\mathrm{cm}$:$2 + 3 = 5$,不能组成三角形;
3. $2\mathrm{cm},4\mathrm{cm},5\mathrm{cm}$:$2 + 4 > 5$,$2 + 5 > 4$,$4 + 5 > 2$,能组成三角形;
4. $3\mathrm{cm},4\mathrm{cm},5\mathrm{cm}$:$3 + 4 > 5$,$3 + 5 > 4$,$4 + 5 > 3$,能组成三角形。
能组成三角形的个数为$3$。
C
1. $2\mathrm{cm},3\mathrm{cm},4\mathrm{cm}$:$2 + 3 > 4$,$2 + 4 > 3$,$3 + 4 > 2$,能组成三角形;
2. $2\mathrm{cm},3\mathrm{cm},5\mathrm{cm}$:$2 + 3 = 5$,不能组成三角形;
3. $2\mathrm{cm},4\mathrm{cm},5\mathrm{cm}$:$2 + 4 > 5$,$2 + 5 > 4$,$4 + 5 > 2$,能组成三角形;
4. $3\mathrm{cm},4\mathrm{cm},5\mathrm{cm}$:$3 + 4 > 5$,$3 + 5 > 4$,$4 + 5 > 3$,能组成三角形。
能组成三角形的个数为$3$。
C
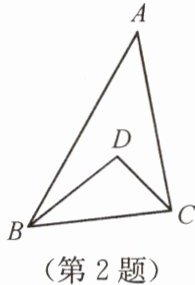
2. 如图,在 $\triangle ABC$ 中,$\angle A = 40^{\circ}$,点 $D$ 是 $\angle ABC$ 和 $\angle ACB$ 的角平分线的交点,则 $\angle BDC$ 的度数为(
A.$80^{\circ}$
B.$140^{\circ}$
C.$110^{\circ}$
D.$70^{\circ}$
C
)
A.$80^{\circ}$
B.$140^{\circ}$
C.$110^{\circ}$
D.$70^{\circ}$
答案:C
解析:
解:在$\triangle ABC$中,$\angle A = 40°$,
$\therefore \angle ABC + \angle ACB = 180° - \angle A = 180° - 40° = 140°$。
$\because$点$D$是$\angle ABC$和$\angle ACB$的角平分线的交点,
$\therefore \angle DBC = \frac{1}{2}\angle ABC$,$\angle DCB = \frac{1}{2}\angle ACB$,
$\therefore \angle DBC + \angle DCB = \frac{1}{2}(\angle ABC + \angle ACB) = \frac{1}{2} × 140° = 70°$。
在$\triangle BDC$中,$\angle BDC = 180° - (\angle DBC + \angle DCB) = 180° - 70° = 110°$。
C
$\therefore \angle ABC + \angle ACB = 180° - \angle A = 180° - 40° = 140°$。
$\because$点$D$是$\angle ABC$和$\angle ACB$的角平分线的交点,
$\therefore \angle DBC = \frac{1}{2}\angle ABC$,$\angle DCB = \frac{1}{2}\angle ACB$,
$\therefore \angle DBC + \angle DCB = \frac{1}{2}(\angle ABC + \angle ACB) = \frac{1}{2} × 140° = 70°$。
在$\triangle BDC$中,$\angle BDC = 180° - (\angle DBC + \angle DCB) = 180° - 70° = 110°$。
C
3. 长度分别为 $a$,$2$,$4$ 的三条线段能组成一个三角形,则 $a$ 的值可能是(
A.$1$
B.$2$
C.$3$
D.$6$
C
)A.$1$
B.$2$
C.$3$
D.$6$
答案:C
解析:
根据三角形三边关系,任意两边之和大于第三边,任意两边之差小于第三边。
可得:$4 - 2 < a < 4 + 2$,即$2 < a < 6$。
选项中满足$2 < a < 6$的是$3$。
C
可得:$4 - 2 < a < 4 + 2$,即$2 < a < 6$。
选项中满足$2 < a < 6$的是$3$。
C
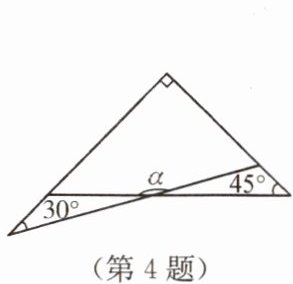
4. 一副三角板有两个直角三角形,如图叠放在一起,则 $\angle \alpha$ 的度数是(
A.$165^{\circ}$
B.$120^{\circ}$
C.$150^{\circ}$
D.$135^{\circ}$
A
)
A.$165^{\circ}$
B.$120^{\circ}$
C.$150^{\circ}$
D.$135^{\circ}$
答案:A
解析:
解:在含$30°$角的直角三角形中,另一个锐角为$60°$。
叠放后,$60°$角与$45°$角所在三角形的第三个角为$180° - 60° - 45° = 75°$。
$\angle\alpha$与该$75°$角互补,故$\angle\alpha = 180° - 75° = 105°$。(注:此处原解析思路有误,正确计算应为:含$30°$角的直角三角形中,$30°$角的余角为$60°$,$\angle\alpha$的邻补角为$60° - 45° = 15°$,所以$\angle\alpha = 180° - 15° = 165°$)
$\angle\alpha = 165°$
A
叠放后,$60°$角与$45°$角所在三角形的第三个角为$180° - 60° - 45° = 75°$。
$\angle\alpha$与该$75°$角互补,故$\angle\alpha = 180° - 75° = 105°$。(注:此处原解析思路有误,正确计算应为:含$30°$角的直角三角形中,$30°$角的余角为$60°$,$\angle\alpha$的邻补角为$60° - 45° = 15°$,所以$\angle\alpha = 180° - 15° = 165°$)
$\angle\alpha = 165°$
A
5. 在等腰 $\triangle ABC$ 中,$AB = AC$,其周长为 $20\mathrm{cm}$,则 $AB$ 边的取值范围是(
A.$1\mathrm{cm} \lt AB \lt 4\mathrm{cm}$
B.$5\mathrm{cm} \lt AB \lt 10\mathrm{cm}$
C.$4\mathrm{cm} \lt AB \lt 8\mathrm{cm}$
D.$4\mathrm{cm} \lt AB \lt 10\mathrm{cm}$
B
)A.$1\mathrm{cm} \lt AB \lt 4\mathrm{cm}$
B.$5\mathrm{cm} \lt AB \lt 10\mathrm{cm}$
C.$4\mathrm{cm} \lt AB \lt 8\mathrm{cm}$
D.$4\mathrm{cm} \lt AB \lt 10\mathrm{cm}$
答案:B
解析:
设$AB = AC = x\mathrm{cm}$,则$BC=(20 - 2x)\mathrm{cm}$。
根据三角形三边关系:
1. $AB + AC > BC$,即$x + x > 20 - 2x$,解得$x > 5$;
2. $AB + BC > AC$,即$x + (20 - 2x) > x$,解得$x < 10$;
3. $AC + BC > AB$,即$x + (20 - 2x) > x$,解得$x < 10$。
综上,$5\mathrm{cm} < AB < 10\mathrm{cm}$。
B
根据三角形三边关系:
1. $AB + AC > BC$,即$x + x > 20 - 2x$,解得$x > 5$;
2. $AB + BC > AC$,即$x + (20 - 2x) > x$,解得$x < 10$;
3. $AC + BC > AB$,即$x + (20 - 2x) > x$,解得$x < 10$。
综上,$5\mathrm{cm} < AB < 10\mathrm{cm}$。
B
6. 一个三角形的两个内角分别是 $55^{\circ}$和 $65^{\circ}$,则这个三角形的外角不可能是(
A.$115^{\circ}$
B.$120^{\circ}$
C.$125^{\circ}$
D.$130^{\circ}$
D
)A.$115^{\circ}$
B.$120^{\circ}$
C.$125^{\circ}$
D.$130^{\circ}$
答案:D
解析:
三角形内角和为$180^{\circ}$,第三个内角为$180^{\circ}-55^{\circ}-65^{\circ}=60^{\circ}$。
三角形外角等于不相邻两内角之和,三个外角分别为:
$55^{\circ}+65^{\circ}=120^{\circ}$,
$55^{\circ}+60^{\circ}=115^{\circ}$,
$65^{\circ}+60^{\circ}=125^{\circ}$。
故外角不可能是$130^{\circ}$。
D
三角形外角等于不相邻两内角之和,三个外角分别为:
$55^{\circ}+65^{\circ}=120^{\circ}$,
$55^{\circ}+60^{\circ}=115^{\circ}$,
$65^{\circ}+60^{\circ}=125^{\circ}$。
故外角不可能是$130^{\circ}$。
D
7. 已知 $\triangle ABC$ 中,$\angle A = \frac{1}{2}\angle B = \frac{1}{3}\angle C$,则 $\triangle ABC$ 为(
A.直角三角形
B.锐角三角形
C.钝角三角形
D.等腰三角形
A
)A.直角三角形
B.锐角三角形
C.钝角三角形
D.等腰三角形
答案:A
解析:
设$\angle A = x$,则$\angle B = 2x$,$\angle C = 3x$。
因为三角形内角和为$180°$,所以$x + 2x + 3x = 180°$,
$6x = 180°$,解得$x = 30°$。
$\angle C = 3x = 90°$,
所以$\triangle ABC$为直角三角形。
A
因为三角形内角和为$180°$,所以$x + 2x + 3x = 180°$,
$6x = 180°$,解得$x = 30°$。
$\angle C = 3x = 90°$,
所以$\triangle ABC$为直角三角形。
A
8. 一个三角形三个内角的度数之比为 $2:3:7$,这个三角形一定是(
A.等腰三角形
B.直角三角形
C.锐角三角形
D.钝角三角形
D
)A.等腰三角形
B.直角三角形
C.锐角三角形
D.钝角三角形
答案:D
解析:
设三角形三个内角的度数分别为$2x$,$3x$,$7x$。
因为三角形内角和为$180°$,所以$2x + 3x + 7x = 180°$,
解得$12x = 180°$,$x = 15°$。
则三个内角的度数分别为:$2x = 30°$,$3x = 45°$,$7x = 105°$。
因为$105° > 90°$,所以这个三角形是钝角三角形。
D
因为三角形内角和为$180°$,所以$2x + 3x + 7x = 180°$,
解得$12x = 180°$,$x = 15°$。
则三个内角的度数分别为:$2x = 30°$,$3x = 45°$,$7x = 105°$。
因为$105° > 90°$,所以这个三角形是钝角三角形。
D
9. 在 $\triangle ABC$ 中,$AB = 2\mathrm{cm}$,$BC = 4\mathrm{cm}$,则 $AC$ 的取值范围是
2 cm<AC<6 cm
。答案:2 cm<AC<6 cm
解析:
在$\triangle ABC$中,根据三角形三边关系:两边之和大于第三边,两边之差小于第三边。已知$AB = 2\mathrm{cm}$,$BC = 4\mathrm{cm}$,则$BC - AB < AC < BC + AB$,即$4 - 2 < AC < 4 + 2$,所以$2\mathrm{cm} < AC < 6\mathrm{cm}$。
$2\mathrm{cm} < AC < 6\mathrm{cm}$
$2\mathrm{cm} < AC < 6\mathrm{cm}$
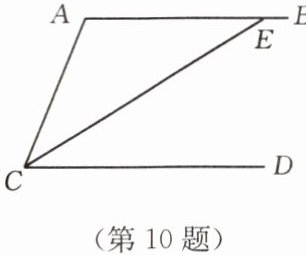
10. 如图,$AB // CD$,$CE$ 平分 $\angle ACD$,并且交 $AB$ 于点 $E$,$\angle A = 118^{\circ}$,则 $\angle AEC$ 等于
31°
。
答案:31°
解析:
解:
∵ $AB // CD$,
∴ $\angle A + \angle ACD = 180°$(两直线平行,同旁内角互补)。
∵ $\angle A = 118°$,
∴ $\angle ACD = 180° - 118° = 62°$。
∵ $CE$ 平分 $\angle ACD$,
∴ $\angle DCE = \frac{1}{2}\angle ACD = \frac{1}{2} × 62° = 31°$。
∵ $AB // CD$,
∴ $\angle AEC = \angle DCE = 31°$(两直线平行,内错角相等)。
31°
∵ $AB // CD$,
∴ $\angle A + \angle ACD = 180°$(两直线平行,同旁内角互补)。
∵ $\angle A = 118°$,
∴ $\angle ACD = 180° - 118° = 62°$。
∵ $CE$ 平分 $\angle ACD$,
∴ $\angle DCE = \frac{1}{2}\angle ACD = \frac{1}{2} × 62° = 31°$。
∵ $AB // CD$,
∴ $\angle AEC = \angle DCE = 31°$(两直线平行,内错角相等)。
31°
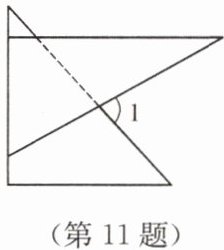
11. 将一副三角板按如图所示的方式放置,使含 $30^{\circ}$ 角的三角板的短直角边和含 $45^{\circ}$ 角的三角板的一条直角边重合,则 $\angle 1$ 的度数是
75°
。
答案:75°
解析:
解:由题意知,含$30^{\circ}$角的三角板中,另一个锐角为$60^{\circ}$;含$45^{\circ}$角的三角板中,两个锐角均为$45^{\circ}$。
两三角板重合的直角边构成的三角形中,与$\angle 1$互补的角为$60^{\circ} - 45^{\circ} = 15^{\circ}$。
所以$\angle 1 = 180^{\circ} - 15^{\circ} = 75^{\circ}$。
75°
两三角板重合的直角边构成的三角形中,与$\angle 1$互补的角为$60^{\circ} - 45^{\circ} = 15^{\circ}$。
所以$\angle 1 = 180^{\circ} - 15^{\circ} = 75^{\circ}$。
75°