12. 在 $\triangle ABC$ 中,$\angle A = 50^{\circ}$,则 $AB$,$AC$ 边上的高所在直线所夹的锐角为
50
度。答案:50
13. 如图,在 $\triangle ABC$ 中,$\angle A = 35^{\circ}$,$\angle C = 60^{\circ}$,$BD$ 平分 $\angle ABC$,$DE // BC$ 交 $AB$ 于点 $E$,则 $\angle BDE = $
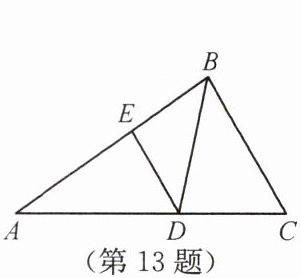
42.5
$^{\circ}$,$\angle BDC = $______77.5
$^{\circ}$。
答案:42.5,77.5
解析:
解:在$\triangle ABC$中,$\angle A=35^{\circ}$,$\angle C=60^{\circ}$,
$\angle ABC=180^{\circ}-\angle A-\angle C=180^{\circ}-35^{\circ}-60^{\circ}=85^{\circ}$。
因为$BD$平分$\angle ABC$,
所以$\angle ABD=\angle DBC=\frac{1}{2}\angle ABC=\frac{1}{2}×85^{\circ}=42.5^{\circ}$。
因为$DE// BC$,
所以$\angle BDE=\angle DBC=42.5^{\circ}$。
在$\triangle BDC$中,$\angle BDC=180^{\circ}-\angle DBC-\angle C=180^{\circ}-42.5^{\circ}-60^{\circ}=77.5^{\circ}$。
$42.5$,$77.5$
$\angle ABC=180^{\circ}-\angle A-\angle C=180^{\circ}-35^{\circ}-60^{\circ}=85^{\circ}$。
因为$BD$平分$\angle ABC$,
所以$\angle ABD=\angle DBC=\frac{1}{2}\angle ABC=\frac{1}{2}×85^{\circ}=42.5^{\circ}$。
因为$DE// BC$,
所以$\angle BDE=\angle DBC=42.5^{\circ}$。
在$\triangle BDC$中,$\angle BDC=180^{\circ}-\angle DBC-\angle C=180^{\circ}-42.5^{\circ}-60^{\circ}=77.5^{\circ}$。
$42.5$,$77.5$
14. 如图,在 $\triangle ABC$ 中,$\angle A = 80^{\circ}$,$\angle ABC$,$\angle ACB$ 的外角平分线交于点 $D$,那么 $\angle BDC = $
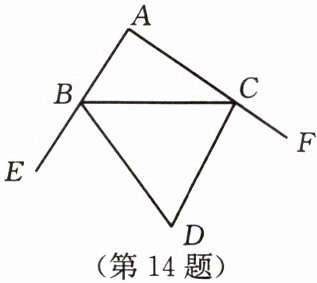
50°
。
答案:50°
解析:
证明:在$\triangle ABC$中,$\angle A = 80°$,
$\therefore \angle ABC + \angle ACB = 180° - \angle A = 100°$,
$\therefore \angle ABC$的外角$= 180° - \angle ABC$,$\angle ACB$的外角$= 180° - \angle ACB$,
$\therefore \angle ABC$的外角$+ \angle ACB$的外角$= 360° - (\angle ABC + \angle ACB) = 260°$,
$\because BD$、$CD$分别平分$\angle ABC$、$\angle ACB$的外角,
$\therefore \angle DBC = \frac{1}{2}\angle ABC$的外角,$\angle DCB = \frac{1}{2}\angle ACB$的外角,
$\therefore \angle DBC + \angle DCB = \frac{1}{2}(\angle ABC$的外角$+ \angle ACB$的外角$) = 130°$,
在$\triangle BDC$中,$\angle BDC = 180° - (\angle DBC + \angle DCB) = 50°$。
$50°$
$\therefore \angle ABC + \angle ACB = 180° - \angle A = 100°$,
$\therefore \angle ABC$的外角$= 180° - \angle ABC$,$\angle ACB$的外角$= 180° - \angle ACB$,
$\therefore \angle ABC$的外角$+ \angle ACB$的外角$= 360° - (\angle ABC + \angle ACB) = 260°$,
$\because BD$、$CD$分别平分$\angle ABC$、$\angle ACB$的外角,
$\therefore \angle DBC = \frac{1}{2}\angle ABC$的外角,$\angle DCB = \frac{1}{2}\angle ACB$的外角,
$\therefore \angle DBC + \angle DCB = \frac{1}{2}(\angle ABC$的外角$+ \angle ACB$的外角$) = 130°$,
在$\triangle BDC$中,$\angle BDC = 180° - (\angle DBC + \angle DCB) = 50°$。
$50°$
15. 等腰三角形的两边长分别为 $3$ 和 $5$,其周长为
11或13
。答案:11或13
解析:
情况一:腰长为3,底边长为5。
$3+3>5$,能构成三角形。
周长为$3+3+5=11$。
情况二:腰长为5,底边长为3。
$5+5>3$,能构成三角形。
周长为$5+5+3=13$。
11或13
$3+3>5$,能构成三角形。
周长为$3+3+5=11$。
情况二:腰长为5,底边长为3。
$5+5>3$,能构成三角形。
周长为$5+5+3=13$。
11或13
16. 如图,$BP$ 是 $\triangle ABC$ 中 $\angle ABC$ 的平分线,$CP$ 是 $\angle ACB$ 的外角的平分线,如果 $\angle ABP = 20^{\circ}$,$\angle ACP = 50^{\circ}$,则 $\angle A + \angle P = $
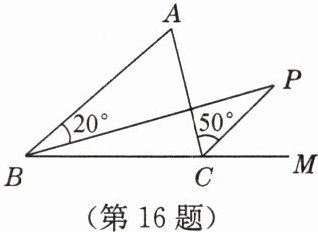
90°
。
答案:90°
解析:
解:
∵BP平分∠ABC,∠ABP=20°,
∴∠ABC=2∠ABP=40°,∠PBC=∠ABP=20°。
∵CP平分∠ACB的外角,∠ACP=50°,
∴∠ACB的外角=2∠ACP=100°,
∴∠ACB=180°-100°=80°。
在△ABC中,∠A=180°-∠ABC-∠ACB=180°-40°-80°=60°。
在△PBC中,∠P=180°-∠PBC-∠PCB,
∠PCB=∠ACB+∠ACP=80°+50°=130°,
∴∠P=180°-20°-130°=30°。
∴∠A+∠P=60°+30°=90°。
90°
∵BP平分∠ABC,∠ABP=20°,
∴∠ABC=2∠ABP=40°,∠PBC=∠ABP=20°。
∵CP平分∠ACB的外角,∠ACP=50°,
∴∠ACB的外角=2∠ACP=100°,
∴∠ACB=180°-100°=80°。
在△ABC中,∠A=180°-∠ABC-∠ACB=180°-40°-80°=60°。
在△PBC中,∠P=180°-∠PBC-∠PCB,
∠PCB=∠ACB+∠ACP=80°+50°=130°,
∴∠P=180°-20°-130°=30°。
∴∠A+∠P=60°+30°=90°。
90°
17. (7 分)等腰三角形的周长是 $12\mathrm{cm}$,一边与另一边的差为 $3\mathrm{cm}$,求三边的长。
答案:5 cm,5 cm,2 cm
解析:
设等腰三角形的腰长为$x\,cm$,底边长为$y\,cm$。
情况一:腰比底长$3\,cm$
$\begin{cases}2x + y = 12 \\ x - y = 3\end{cases}$
解得$\begin{cases}x = 5 \\ y = 2\end{cases}$
此时三边为$5\,cm,5\,cm,2\,cm$,满足三角形三边关系。
情况二:底比腰长$3\,cm$
$\begin{cases}2x + y = 12 \\ y - x = 3\end{cases}$
解得$\begin{cases}x = 3 \\ y = 6\end{cases}$
此时三边为$3\,cm,3\,cm,6\,cm$,因$3 + 3 = 6$,不满足三角形三边关系,舍去。
综上,三边的长为$5\,cm,5\,cm,2\,cm$。
情况一:腰比底长$3\,cm$
$\begin{cases}2x + y = 12 \\ x - y = 3\end{cases}$
解得$\begin{cases}x = 5 \\ y = 2\end{cases}$
此时三边为$5\,cm,5\,cm,2\,cm$,满足三角形三边关系。
情况二:底比腰长$3\,cm$
$\begin{cases}2x + y = 12 \\ y - x = 3\end{cases}$
解得$\begin{cases}x = 3 \\ y = 6\end{cases}$
此时三边为$3\,cm,3\,cm,6\,cm$,因$3 + 3 = 6$,不满足三角形三边关系,舍去。
综上,三边的长为$5\,cm,5\,cm,2\,cm$。
18. (7 分)如图,$\angle A = 70^{\circ}$,$\angle ABE = 35^{\circ}$,$\angle ACD = 25^{\circ}$。求 $\angle BFC$ 的度数。
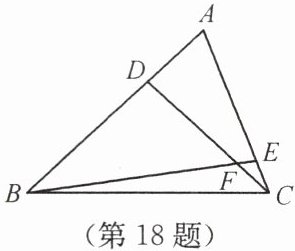

答案:130°
解析:
证明:在△ABC中,∠A=70°,
∴∠ABC+∠ACB=180°-∠A=110°。
∵∠ABE=35°,∠ACD=25°,
∴∠EBC+∠FCB=∠ABC+∠ACB-∠ABE-∠ACD=110°-35°-25°=50°。
在△BFC中,∠BFC=180°-(∠EBC+∠FCB)=180°-50°=130°。
故∠BFC的度数为130°。
∴∠ABC+∠ACB=180°-∠A=110°。
∵∠ABE=35°,∠ACD=25°,
∴∠EBC+∠FCB=∠ABC+∠ACB-∠ABE-∠ACD=110°-35°-25°=50°。
在△BFC中,∠BFC=180°-(∠EBC+∠FCB)=180°-50°=130°。
故∠BFC的度数为130°。
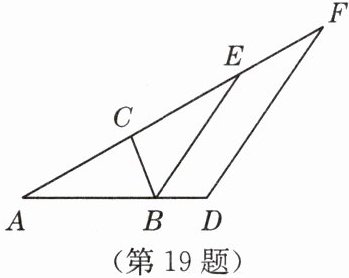
19. (7 分)如图,在 $\triangle ABC$ 中,$\angle A = 30^{\circ}$,$\angle ACB = 80^{\circ}$,$\triangle ABC$ 的外角 $\angle CBD$ 的平分线 $BE$ 交 $AC$ 的延长线于点 $E$。
(1)求 $\angle CBE$ 的度数。
(2)过点 $D$ 作 $DF // BE$,交 $AC$ 的延长线于点 $F$,求 $\angle F$ 的度数。
(1)求 $\angle CBE$ 的度数。
(2)过点 $D$ 作 $DF // BE$,交 $AC$ 的延长线于点 $F$,求 $\angle F$ 的度数。

答案:(1)∠CBE=55°;(2)∠F=25°
解析:
(1) 在$\triangle ABC$中,$\angle A=30^{\circ}$,$\angle ACB=80^{\circ}$,根据三角形内角和定理,$\angle ABC=180^{\circ}-\angle A-\angle ACB=180^{\circ}-30^{\circ}-80^{\circ}=70^{\circ}$。
$\angle CBD$是$\triangle ABC$的外角,所以$\angle CBD=180^{\circ}-\angle ABC=180^{\circ}-70^{\circ}=110^{\circ}$。
因为$BE$平分$\angle CBD$,所以$\angle CBE=\frac{1}{2}\angle CBD=\frac{1}{2}×110^{\circ}=55^{\circ}$。
(2) 由
(1)知$\angle ABC=70^{\circ}$,$\angle CBE=55^{\circ}$,则$\angle ABE=\angle ABC+\angle CBE=70^{\circ}+55^{\circ}=125^{\circ}$。
在$\triangle ABE$中,$\angle A=30^{\circ}$,所以$\angle AEB=180^{\circ}-\angle A-\angle ABE=180^{\circ}-30^{\circ}-125^{\circ}=25^{\circ}$。
因为$DF// BE$,所以$\angle F=\angle AEB=25^{\circ}$(两直线平行,同位角相等)。
答案:
(1)$55^{\circ}$;
(2)$25^{\circ}$
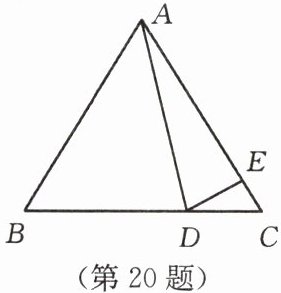
20. (7 分)如图,在 $\triangle ABC$ 中,$\angle B = \angle C$,$\angle CDE = 20^{\circ}$,且 $\angle ADE = \angle AED$,求 $\angle BAD$ 的度数。

40°
答案:40°
解析:
证明:设$\angle BAD = x$,$\angle B = \angle C = y$。
$\because \angle CDE = 20^{\circ}$,$\angle ADE = \angle AED$,
$\therefore \angle ADE = \angle AED = \angle CDE + \angle C = 20^{\circ} + y$。
$\because \angle AED + \angle DEC = 180^{\circ}$,
$\therefore \angle DEC = 180^{\circ} - \angle AED = 180^{\circ} - (20^{\circ} + y) = 160^{\circ} - y$。
在$\triangle DEC$中,$\angle CDE + \angle C + \angle DEC = 180^{\circ}$,
即$20^{\circ} + y + (160^{\circ} - y) = 180^{\circ}$,恒成立。
在$\triangle ABD$中,$\angle ADC = \angle B + \angle BAD = y + x$。
又$\angle ADC = \angle ADE + \angle CDE$,
$\therefore y + x = (20^{\circ} + y) + 20^{\circ}$,
解得$x = 40^{\circ}$。
$\angle BAD = 40^{\circ}$。
$\because \angle CDE = 20^{\circ}$,$\angle ADE = \angle AED$,
$\therefore \angle ADE = \angle AED = \angle CDE + \angle C = 20^{\circ} + y$。
$\because \angle AED + \angle DEC = 180^{\circ}$,
$\therefore \angle DEC = 180^{\circ} - \angle AED = 180^{\circ} - (20^{\circ} + y) = 160^{\circ} - y$。
在$\triangle DEC$中,$\angle CDE + \angle C + \angle DEC = 180^{\circ}$,
即$20^{\circ} + y + (160^{\circ} - y) = 180^{\circ}$,恒成立。
在$\triangle ABD$中,$\angle ADC = \angle B + \angle BAD = y + x$。
又$\angle ADC = \angle ADE + \angle CDE$,
$\therefore y + x = (20^{\circ} + y) + 20^{\circ}$,
解得$x = 40^{\circ}$。
$\angle BAD = 40^{\circ}$。