21. (12 分)【探索归纳】
(1)如图(1),已知 $\triangle ABC$ 为直角三角形,$\angle A = 90^{\circ}$,若沿图中虚线剪去 $\angle A$,则 $\angle 1 + \angle 2 = $
(2)如图(2),已知在 $\triangle ABC$ 中,$\angle A = 40^{\circ}$,剪去 $\angle A$ 后成四边形,则 $\angle 1 + \angle 2 = $
(3)如图(2),根据(1)与(2)的求解过程,请你归纳猜想 $\angle 1 + \angle 2$ 与 $\angle A$ 的关系是
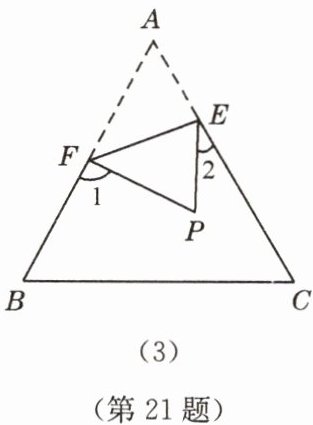
(4)如图(3),若没有剪掉 $\angle A$,而是把它折成如图所示形状,试探究 $\angle 1 + \angle 2$ 与 $\angle A$ 的关系并说明理由。
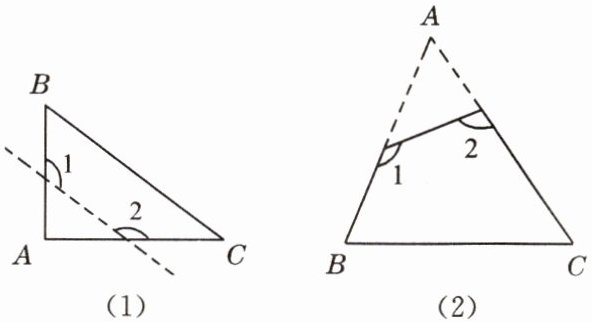
(1)如图(1),已知 $\triangle ABC$ 为直角三角形,$\angle A = 90^{\circ}$,若沿图中虚线剪去 $\angle A$,则 $\angle 1 + \angle 2 = $
270°
。(2)如图(2),已知在 $\triangle ABC$ 中,$\angle A = 40^{\circ}$,剪去 $\angle A$ 后成四边形,则 $\angle 1 + \angle 2 = $
220°
。(3)如图(2),根据(1)与(2)的求解过程,请你归纳猜想 $\angle 1 + \angle 2$ 与 $\angle A$ 的关系是
∠1+∠2=180°+∠A
。(4)如图(3),若没有剪掉 $\angle A$,而是把它折成如图所示形状,试探究 $\angle 1 + \angle 2$ 与 $\angle A$ 的关系并说明理由。


答案:(1)270°;(2)220°;(3)∠1+∠2=180°+∠A;(4)
∵△EFP是由△EFA折叠得到的,
∴∠AFE=∠PFE,∠AEF=∠PEF,
∴∠1=180°-2∠AFE,∠2=180°-2∠AEF,
∴∠1+∠2=360°-2(∠AFE+∠AEF). 又
∵∠AFE+∠AEF=180°-∠A,
∴∠1+∠2=360°-2(180°-∠A)=2∠A.
∵△EFP是由△EFA折叠得到的,
∴∠AFE=∠PFE,∠AEF=∠PEF,
∴∠1=180°-2∠AFE,∠2=180°-2∠AEF,
∴∠1+∠2=360°-2(∠AFE+∠AEF). 又
∵∠AFE+∠AEF=180°-∠A,
∴∠1+∠2=360°-2(180°-∠A)=2∠A.
22. (12 分)【问题引入】
(1)如图(1),在 $\triangle ABC$ 中,点 $O$ 是 $\angle ABC$ 和 $\angle ACB$ 平分线的交点,若 $\angle A = \alpha$,则 $\angle BOC = $
(2)如图(2),$\angle CBO = \frac{1}{3}\angle ABC$,$\angle BCO = \frac{1}{3}\angle ACB$,若 $\angle A = \alpha$,则 $\angle BOC = $
(3)如图(3),$\angle CBO = \frac{1}{3}\angle DBC$,$\angle BCO = \frac{1}{3}\angle ECB$,若 $\angle A = \alpha$,请猜想 $\angle BOC = $
【类比研究】
(4)若 $BO$,$CO$ 分别是 $\triangle ABC$ 的外角 $\angle DBC$,$\angle ECB$ 的 $n$ 等分线,它们交于点 $O$,$\angle CBO = \frac{1}{n}\angle DBC$,$\angle BCO = \frac{1}{n}\angle ECB$。若 $\angle A = \alpha$,请猜想 $\angle BOC = $
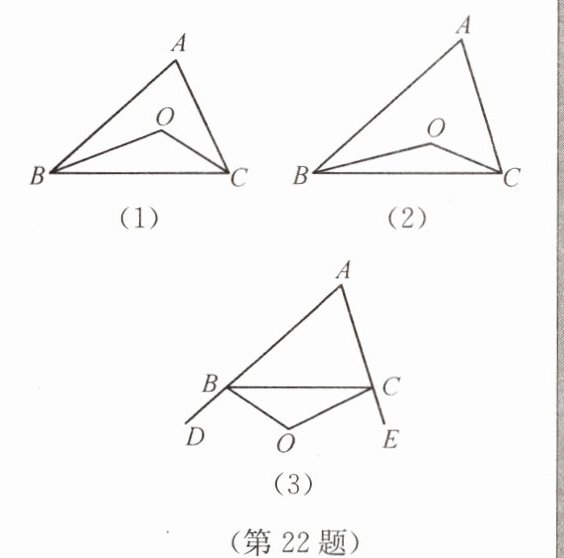
(1)如图(1),在 $\triangle ABC$ 中,点 $O$ 是 $\angle ABC$ 和 $\angle ACB$ 平分线的交点,若 $\angle A = \alpha$,则 $\angle BOC = $
90°+$\frac{\alpha}{2}$
(用 $\alpha$ 表示)。(2)如图(2),$\angle CBO = \frac{1}{3}\angle ABC$,$\angle BCO = \frac{1}{3}\angle ACB$,若 $\angle A = \alpha$,则 $\angle BOC = $
120°+$\frac{\alpha}{3}$
(用 $\alpha$ 表示),并说明理由。(3)如图(3),$\angle CBO = \frac{1}{3}\angle DBC$,$\angle BCO = \frac{1}{3}\angle ECB$,若 $\angle A = \alpha$,请猜想 $\angle BOC = $
120°-$\frac{\alpha}{3}$
(用 $\alpha$ 表示),并说明理由。【类比研究】
(4)若 $BO$,$CO$ 分别是 $\triangle ABC$ 的外角 $\angle DBC$,$\angle ECB$ 的 $n$ 等分线,它们交于点 $O$,$\angle CBO = \frac{1}{n}\angle DBC$,$\angle BCO = \frac{1}{n}\angle ECB$。若 $\angle A = \alpha$,请猜想 $\angle BOC = $
$\frac{n-1}{n}$·180°-$\frac{\alpha}{n}$
(用 $\alpha$,$n$ 表示,直接写出结果)。
答案:(1)90°+$\frac{\alpha}{2}$. (2)120°+$\frac{\alpha}{3}$. 理由:∠BOC=180°-(∠OBC+∠OCB)=180°-$\frac{1}{3}$(∠ABC+∠ACB)=180°-$\frac{1}{3}$(180°-∠A)=120°+$\frac{\alpha}{3}$.(3)120°-$\frac{\alpha}{3}$. 理由:∠BOC=180°-(∠OBC+∠OCB)=180°-$\frac{1}{3}$(∠DBC+∠ECB)=180°-$\frac{1}{3}$(180°+∠A)=120°-$\frac{\alpha}{3}$.(4)$\frac{n-1}{n}$·180°-$\frac{\alpha}{n}$.
解析:
(1)$90°+\frac{\alpha}{2}$
(2)$120°+\frac{\alpha}{3}$
证明:$\angle BOC=180°-(\angle OBC+\angle OCB)$
$=180°-\frac{1}{3}(\angle ABC+\angle ACB)$
$=180°-\frac{1}{3}(180°-\angle A)$
$=180°-\frac{1}{3}(180°-\alpha)$
$=120°+\frac{\alpha}{3}$
(3)$120°-\frac{\alpha}{3}$
证明:$\angle BOC=180°-(\angle OBC+\angle OCB)$
$=180°-\frac{1}{3}(\angle DBC+\angle ECB)$
$=180°-\frac{1}{3}(180°+\angle A)$
$=180°-\frac{1}{3}(180°+\alpha)$
$=120°-\frac{\alpha}{3}$
(4)$\frac{n-1}{n}\cdot180°-\frac{\alpha}{n}$
(2)$120°+\frac{\alpha}{3}$
证明:$\angle BOC=180°-(\angle OBC+\angle OCB)$
$=180°-\frac{1}{3}(\angle ABC+\angle ACB)$
$=180°-\frac{1}{3}(180°-\angle A)$
$=180°-\frac{1}{3}(180°-\alpha)$
$=120°+\frac{\alpha}{3}$
(3)$120°-\frac{\alpha}{3}$
证明:$\angle BOC=180°-(\angle OBC+\angle OCB)$
$=180°-\frac{1}{3}(\angle DBC+\angle ECB)$
$=180°-\frac{1}{3}(180°+\angle A)$
$=180°-\frac{1}{3}(180°+\alpha)$
$=120°-\frac{\alpha}{3}$
(4)$\frac{n-1}{n}\cdot180°-\frac{\alpha}{n}$