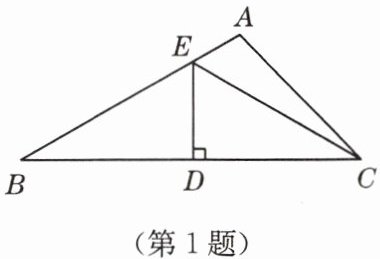
1. 如图,在 $ \triangle ABC $ 中,$ \angle B = 30^{\circ} $,$ ED $ 垂直平分 $ BC $,$ ED = 3 $,则 $ CE $ 的长为
6
。
答案:6
解析:
证明:
∵ED垂直平分BC,
∴EB=EC,∠EDB=90°。
∵∠B=30°,ED=3,
在Rt△BDE中,∠B=30°,
∴EB=2ED=2×3=6。
∵EB=EC,
∴CE=6。
6
∵ED垂直平分BC,
∴EB=EC,∠EDB=90°。
∵∠B=30°,ED=3,
在Rt△BDE中,∠B=30°,
∴EB=2ED=2×3=6。
∵EB=EC,
∴CE=6。
6
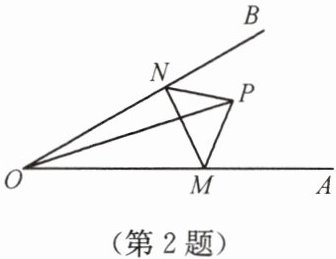
2. 如图,点 $ P $ 是 $ \angle AOB $ 内任意一点,$ OP = 5\ cm $,点 $ M $ 和点 $ N $ 分别是射线 $ OA $ 和射线 $ OB $ 上的动点,$ \triangle PMN $ 周长的最小值是 $ 5\ cm $,则 $ \angle AOB = $
30
$^{\circ} $。
答案:30
解析:
解:分别作点 $ P $ 关于 $ OA $、$ OB $ 的对称点 $ P_1 $、$ P_2 $,连接 $ P_1P_2 $,交 $ OA $ 于 $ M $,交 $ OB $ 于 $ N $,连接 $ OP_1 $、$ OP_2 $、$ PM $、$ PN $。
由对称性质得:$ PM = P_1M $,$ PN = P_2N $,$ OP_1 = OP = OP_2 = 5\ cm $,$ \angle P_1OA = \angle POA $,$ \angle P_2OB = \angle POB $。
$ \triangle PMN $ 周长 $ = PM + MN + PN = P_1M + MN + P_2N = P_1P_2 $,其最小值为 $ 5\ cm $,即 $ P_1P_2 = 5\ cm $。
在 $ \triangle OP_1P_2 $ 中,$ OP_1 = OP_2 = P_1P_2 = 5\ cm $,故 $ \triangle OP_1P_2 $ 为等边三角形,$ \angle P_1OP_2 = 60° $。
$ \angle AOB = \angle POA + \angle POB = \frac{1}{2}\angle P_1OP_2 = 30° $。
$ 30 $
由对称性质得:$ PM = P_1M $,$ PN = P_2N $,$ OP_1 = OP = OP_2 = 5\ cm $,$ \angle P_1OA = \angle POA $,$ \angle P_2OB = \angle POB $。
$ \triangle PMN $ 周长 $ = PM + MN + PN = P_1M + MN + P_2N = P_1P_2 $,其最小值为 $ 5\ cm $,即 $ P_1P_2 = 5\ cm $。
在 $ \triangle OP_1P_2 $ 中,$ OP_1 = OP_2 = P_1P_2 = 5\ cm $,故 $ \triangle OP_1P_2 $ 为等边三角形,$ \angle P_1OP_2 = 60° $。
$ \angle AOB = \angle POA + \angle POB = \frac{1}{2}\angle P_1OP_2 = 30° $。
$ 30 $