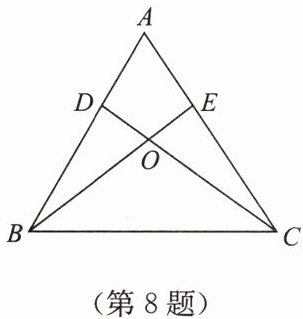
8. 如图,△ABC的两条高BE,CD相交于点O,且OB= OC,∠A= 60°。
(1)求证:△ABC是等边三角形;
(2)判断点O是否在∠BAC的平分线上?并说明理由。
(1)求证:△ABC是等边三角形;
(2)判断点O是否在∠BAC的平分线上?并说明理由。

答案:
(1)证明:
∵OB=OC,
∴∠EBC=∠DCB.
∵BE⊥AC,CD⊥AB,
∴∠BEC=∠CDB=90°.在△BCE和△CBD中,$\left\{\begin{array}{l} ∠EBC=∠DCB,\\ ∠BEC=∠CDB,\\ BC=CB,\end{array}\right.$
∴△BCE≌△CBD(AAS),
∴∠DBC=∠ECB,
∴AB=AC.又
∵∠A=60°,
∴△ABC是等边三角形.
(2)点O在∠BAC的平分线上,理由如下:连接AO,由
(1)可知△BCE≌△CBD,
∴EB=CD.
∵OB=OC,
∴OE=OD,又
∵OE⊥AC,OD⊥AB,
∴点O在∠BAC的平分线上.
(1)证明:
∵OB=OC,
∴∠EBC=∠DCB.
∵BE⊥AC,CD⊥AB,
∴∠BEC=∠CDB=90°.在△BCE和△CBD中,$\left\{\begin{array}{l} ∠EBC=∠DCB,\\ ∠BEC=∠CDB,\\ BC=CB,\end{array}\right.$
∴△BCE≌△CBD(AAS),
∴∠DBC=∠ECB,
∴AB=AC.又
∵∠A=60°,
∴△ABC是等边三角形.
(2)点O在∠BAC的平分线上,理由如下:连接AO,由
(1)可知△BCE≌△CBD,
∴EB=CD.
∵OB=OC,
∴OE=OD,又
∵OE⊥AC,OD⊥AB,
∴点O在∠BAC的平分线上.
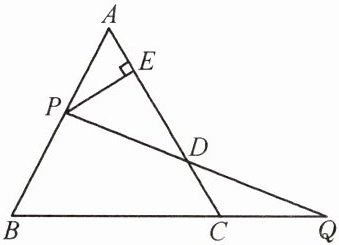
如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于点E,Q为BC延长线上一点,当PA= CQ时,连PQ交AC边于点D,则DE的长为(
A.$\frac{1}{3}$
B.$\frac{1}{2}$
C.$\frac{2}{3}$
D.$\frac{3}{5}$
B
)
A.$\frac{1}{3}$
B.$\frac{1}{2}$
C.$\frac{2}{3}$
D.$\frac{3}{5}$
答案:B
解析:
证明:过点P作PF//BC交AC于点F。
∵△ABC是等边三角形,
∴∠A=∠B=∠ACB=60°。
∵PF//BC,
∴∠AFP=∠ACB=60°,∠PFD=∠QCD,
∴△APF是等边三角形,
∴PA=PF=AF。
∵PA=CQ,
∴PF=CQ。
在△PFD和△QCD中,
$\left\{\begin{array}{l} ∠PFD=∠QCD \\ ∠PDF=∠QDC \\ PF=CQ\end{array}\right.$,
∴△PFD≌△QCD(AAS),
∴FD=CD。
∵PE⊥AC,△APF是等边三角形,
∴AE=EF。
∵AE=EF,FD=CD,
∴EF+FD=AE+CD,
∴ED=AE+CD。
∵AC=AE+ED+CD=1,
∴ED+ED=1,
∴ED=$\frac{1}{2}$。
答案:B
∵△ABC是等边三角形,
∴∠A=∠B=∠ACB=60°。
∵PF//BC,
∴∠AFP=∠ACB=60°,∠PFD=∠QCD,
∴△APF是等边三角形,
∴PA=PF=AF。
∵PA=CQ,
∴PF=CQ。
在△PFD和△QCD中,
$\left\{\begin{array}{l} ∠PFD=∠QCD \\ ∠PDF=∠QDC \\ PF=CQ\end{array}\right.$,
∴△PFD≌△QCD(AAS),
∴FD=CD。
∵PE⊥AC,△APF是等边三角形,
∴AE=EF。
∵AE=EF,FD=CD,
∴EF+FD=AE+CD,
∴ED=AE+CD。
∵AC=AE+ED+CD=1,
∴ED+ED=1,
∴ED=$\frac{1}{2}$。
答案:B
1. 两点的所有连线中,
线段
最短。答案:线段
2. 连接直线外一点与直线上各点的所有线段中,
垂线段
最短。答案:垂线段
3. 如果两个图形关于某条直线对称,那么
对称轴
是任何一对对应点所连线段的垂直平分线。答案:对称轴
4. 点 $ A $,$ B $ 分别是直线 $ l $ 异侧的两个点,如何在 $ l $ 上找到一点 $ P $,使 $ P $ 到点 $ A $、点 $ B $ 的距离和最小?并简述理由。
连接AB,与直线l交点即为点P. 依据“两点之间,线段最短”
。答案:连接AB,与直线l交点即为点P. 依据“两点之间,线段最短”
问题 如图(1),要在燃气管道 $ l $ 上修建一个泵站,分别向 $ A $,$ B $ 两镇供气。泵站修在管道的什么地方,可使所用的输气管线最短?你可以在 $ l $ 上找几个点试一试,能发现什么规律?
聪明的小华通过独立思考,很快得出了解决这个问题的正确办法。他把管道 $ l $ 看成一条直线(如图(2)),问题就转化为,要在直线 $ l $ 上找一点 $ P $,使 $ AP $ 与 $ BP $ 的和最小。他的作法是这样的:
① 作点 $ B $ 关于直线 $ l $ 的对称点 $ B' $;
② 连接 $ AB' $ 交直线 $ l $ 于点 $ P $,则点 $ P $ 为所求。
请你参考小华的作法解决下列问题。
如图(3),在 $ \triangle ABC $ 中,点 $ D $,$ E $ 分别是 $ AB $,$ AC $ 边的中点,请你在 $ BC $ 边上确定一点 $ P $,使 $ \triangle PDE $ 的周长最小。
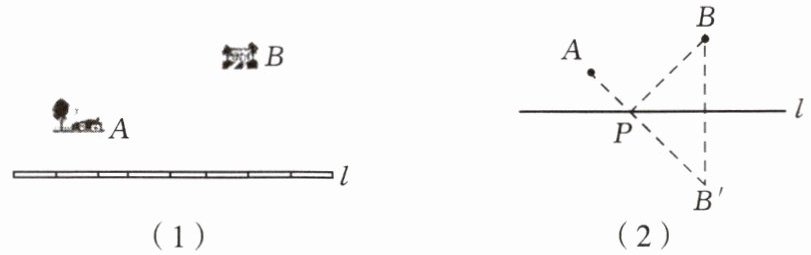
聪明的小华通过独立思考,很快得出了解决这个问题的正确办法。他把管道 $ l $ 看成一条直线(如图(2)),问题就转化为,要在直线 $ l $ 上找一点 $ P $,使 $ AP $ 与 $ BP $ 的和最小。他的作法是这样的:
① 作点 $ B $ 关于直线 $ l $ 的对称点 $ B' $;
② 连接 $ AB' $ 交直线 $ l $ 于点 $ P $,则点 $ P $ 为所求。
请你参考小华的作法解决下列问题。
如图(3),在 $ \triangle ABC $ 中,点 $ D $,$ E $ 分别是 $ AB $,$ AC $ 边的中点,请你在 $ BC $ 边上确定一点 $ P $,使 $ \triangle PDE $ 的周长最小。
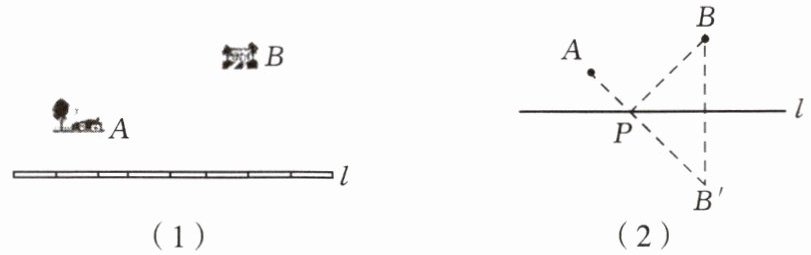
答案:1. 作法:
作点$E$关于$BC$的对称点$E'$;
连接$DE'$并交$BC$于点$P$,则点$P$为所求。
2. 理由:
因为点$D$,$E$分别是$AB$,$AC$边的中点,根据三角形中位线定理,$DE// BC$且$DE =\frac{1}{2}BC$。
根据两点之间线段最短,在$\triangle PDE$中,$DP + PE=DP + PE'$,当$D$,$P$,$E'$在同一条直线上时,$DP + PE$的值最小,此时$\triangle PDE$的周长$C = DE+DP + PE$也最小。
所以,按上述作法在$BC$边上确定的点$P$能使$\triangle PDE$的周长最小。
作点$E$关于$BC$的对称点$E'$;
连接$DE'$并交$BC$于点$P$,则点$P$为所求。
2. 理由:
因为点$D$,$E$分别是$AB$,$AC$边的中点,根据三角形中位线定理,$DE// BC$且$DE =\frac{1}{2}BC$。
根据两点之间线段最短,在$\triangle PDE$中,$DP + PE=DP + PE'$,当$D$,$P$,$E'$在同一条直线上时,$DP + PE$的值最小,此时$\triangle PDE$的周长$C = DE+DP + PE$也最小。
所以,按上述作法在$BC$边上确定的点$P$能使$\triangle PDE$的周长最小。