1. 有下列给出的三角形:(1)三个外角都相等的三角形;(2)有两个内角为60°的三角形;(3)一边上的高也是这条边上的中线的三角形;(4)有一个角是60°的等腰三角形。其中是等边三角形的个数有(
A.4个
B.3个
C.2个
D.1个
B
)A.4个
B.3个
C.2个
D.1个
答案:B
解析:
(1)三个外角都相等,则三个内角都相等,是等边三角形;
(2)有两个内角为60°,则第三个内角为180°-60°-60°=60°,三个内角都相等,是等边三角形;
(3)一边上的高也是这条边上的中线的三角形是等腰三角形,不一定是等边三角形;
(4)有一个角是60°的等腰三角形是等边三角形。
是等边三角形的有
(1)
(2)
(4),共3个。
B
2. 如图,已知∠AOB= 30°,点P在∠AOB内部$,P_1$与P关于OB对称$,P_2$与P关于OA对称,则$P_1,O,P_2$三点所构成的三角形的三个内角的大小关系是
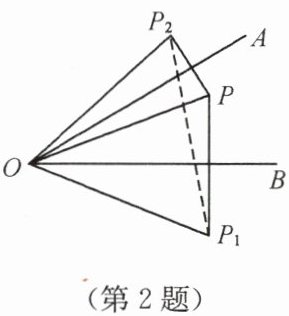
相等
。
答案:相等
解析:
证明:连接OP。
∵点P₁与P关于OB对称,
∴OP₁=OP,∠P₁OB=∠POB。
∵点P₂与P关于OA对称,
∴OP₂=OP,∠P₂OA=∠POA。
∵∠AOB=30°,
∴∠P₁OP₂=∠P₁OB+∠POB+∠P₂OA+∠POA=2(∠POA+∠POB)=2∠AOB=60°。
∵OP₁=OP₂,∠P₁OP₂=60°,
∴△P₁OP₂是等边三角形。
∴△P₁OP₂的三个内角都等于60°,即三个内角相等。
相等
∵点P₁与P关于OB对称,
∴OP₁=OP,∠P₁OB=∠POB。
∵点P₂与P关于OA对称,
∴OP₂=OP,∠P₂OA=∠POA。
∵∠AOB=30°,
∴∠P₁OP₂=∠P₁OB+∠POB+∠P₂OA+∠POA=2(∠POA+∠POB)=2∠AOB=60°。
∵OP₁=OP₂,∠P₁OP₂=60°,
∴△P₁OP₂是等边三角形。
∴△P₁OP₂的三个内角都等于60°,即三个内角相等。
相等
3. 如图,△ABC是等边三角形,点D,E,F分别在AB,BC,CA的延长线上,且BD= CE= AF,则△DEF的三边大小关系是
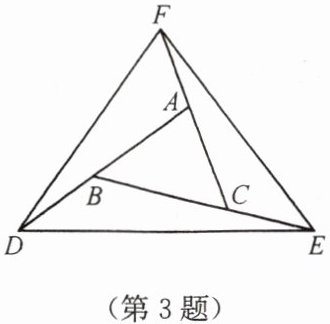
相等
。
答案:相等
解析:
证明:
∵△ABC是等边三角形,
∴AB=BC=CA,∠BAC=∠ABC=∠ACB=60°,
∴∠FAD=∠DBE=∠ECF=120°。
∵BD=CE=AF,
设AB=BC=CA=a,BD=CE=AF=b,
则AD=AB+BD=a+b,BE=BC+CE=a+b,CF=CA+AF=a+b,
∴AD=BE=CF。
在△FAD和△DBE中,
AF=BD,∠FAD=∠DBE,AD=BE,
∴△FAD≌△DBE(SAS),
∴FD=ED。
同理可证△DBE≌△ECF(SAS),
∴ED=FE。
∴FD=ED=FE,即△DEF的三边相等。
相等
∵△ABC是等边三角形,
∴AB=BC=CA,∠BAC=∠ABC=∠ACB=60°,
∴∠FAD=∠DBE=∠ECF=120°。
∵BD=CE=AF,
设AB=BC=CA=a,BD=CE=AF=b,
则AD=AB+BD=a+b,BE=BC+CE=a+b,CF=CA+AF=a+b,
∴AD=BE=CF。
在△FAD和△DBE中,
AF=BD,∠FAD=∠DBE,AD=BE,
∴△FAD≌△DBE(SAS),
∴FD=ED。
同理可证△DBE≌△ECF(SAS),
∴ED=FE。
∴FD=ED=FE,即△DEF的三边相等。
相等
4. 如图,在Rt△ABC中,∠C= 90°,∠CAB的平分线交BC于点D,DE是AB的垂直平分线,垂足为E。若BC= 3,则DE的长为
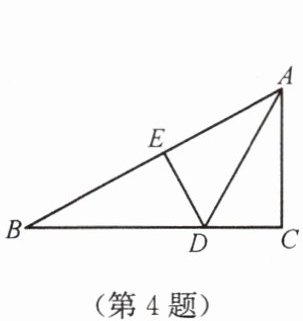
1
。
答案:1
解析:
证明:
∵DE是AB的垂直平分线,
∴DA=DB,∠B=∠DAB。
∵AD平分∠CAB,
∴∠CAD=∠DAB=∠B。
在Rt△ABC中,∠C=90°,
∴∠CAD+∠DAB+∠B=90°,
即3∠B=90°,∠B=30°。
∵AD平分∠CAB,DC⊥AC,DE⊥AB,
∴DC=DE。
设DE=DC=x,则DB=3-x。
在Rt△BDE中,∠B=30°,
∴DE=1/2 DB,即x=1/2 (3-x),
解得x=1。
故DE的长为1。
1
∵DE是AB的垂直平分线,
∴DA=DB,∠B=∠DAB。
∵AD平分∠CAB,
∴∠CAD=∠DAB=∠B。
在Rt△ABC中,∠C=90°,
∴∠CAD+∠DAB+∠B=90°,
即3∠B=90°,∠B=30°。
∵AD平分∠CAB,DC⊥AC,DE⊥AB,
∴DC=DE。
设DE=DC=x,则DB=3-x。
在Rt△BDE中,∠B=30°,
∴DE=1/2 DB,即x=1/2 (3-x),
解得x=1。
故DE的长为1。
1
5. 已知一个三角形任何一个内角的平分线都垂直于这个角的对边,这个三角形是
等边三角形
。答案:等边三角形
6. 如图,△ABC是等边三角形,点D,E,F分别在AB,BC,CA上,且AD= BE= CF。求证:△DEF是等边三角形。
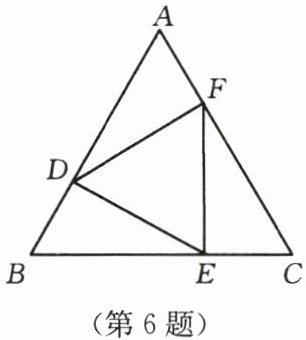

答案:证明:
∵△ABC是等边三角形,
∴AB=BC=CA,∠A=∠B=∠C=60°.
∵AD=BE=CF,
∴BD=CE=AF.在△ADF和△BED中,$\left\{\begin{array}{l} AD=BE,\\ ∠A=∠B,\\ AF=BD,\end{array}\right.$
∴△ADF≌△BED.
∴DF=ED.同理可证DF=FE.
∴DF=ED=FE.
∴△DEF是等边三角形.
∵△ABC是等边三角形,
∴AB=BC=CA,∠A=∠B=∠C=60°.
∵AD=BE=CF,
∴BD=CE=AF.在△ADF和△BED中,$\left\{\begin{array}{l} AD=BE,\\ ∠A=∠B,\\ AF=BD,\end{array}\right.$
∴△ADF≌△BED.
∴DF=ED.同理可证DF=FE.
∴DF=ED=FE.
∴△DEF是等边三角形.
7. 如图,在△ABC中,∠B= 2∠C,BC= 2AB,AD是中线。求证:△ABD是等边三角形。

答案:提示:作∠ABC的平分线BE交AC于点E,连接ED.证△ABE≌△DBE(SAS),得∠BAE=∠BDE=90°,最后得∠ABC=60°.
解析:
证明:作∠ABC的平分线BE交AC于点E,连接ED。
∵BE平分∠ABC,∠ABC=2∠C,
∴∠ABE=∠EBC=∠C。
∴EB=EC。
∵AD是中线,BC=2AB,
∴BD=DC=AB。
在△ABE和△DBE中,
AB=DB,∠ABE=∠DBE,BE=BE,
∴△ABE≌△DBE(SAS)。
∴∠BAE=∠BDE。
设∠C=α,则∠ABC=2α,∠BAC=180°-3α。
∴∠BDE=180°-3α。
∵∠BDE+∠EDC=180°,
∴∠EDC=3α。
∵EB=EC,ED=ED,DB=DC,
∴△EDB≌△EDC(SSS)。
∴∠EDB=∠EDC。
∴180°-3α=3α,解得α=30°。
∴∠ABC=60°。
∵AB=BD,∠ABD=60°,
∴△ABD是等边三角形。
∵BE平分∠ABC,∠ABC=2∠C,
∴∠ABE=∠EBC=∠C。
∴EB=EC。
∵AD是中线,BC=2AB,
∴BD=DC=AB。
在△ABE和△DBE中,
AB=DB,∠ABE=∠DBE,BE=BE,
∴△ABE≌△DBE(SAS)。
∴∠BAE=∠BDE。
设∠C=α,则∠ABC=2α,∠BAC=180°-3α。
∴∠BDE=180°-3α。
∵∠BDE+∠EDC=180°,
∴∠EDC=3α。
∵EB=EC,ED=ED,DB=DC,
∴△EDB≌△EDC(SSS)。
∴∠EDB=∠EDC。
∴180°-3α=3α,解得α=30°。
∴∠ABC=60°。
∵AB=BD,∠ABD=60°,
∴△ABD是等边三角形。