1.
三个角
都相等的三角形是等边三角形。答案:三个角
2.
有一个角是60°
的等腰三角形是等边三角形。答案:有一个角是60°
3. 在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于
斜边的一半
。答案:斜边的一半
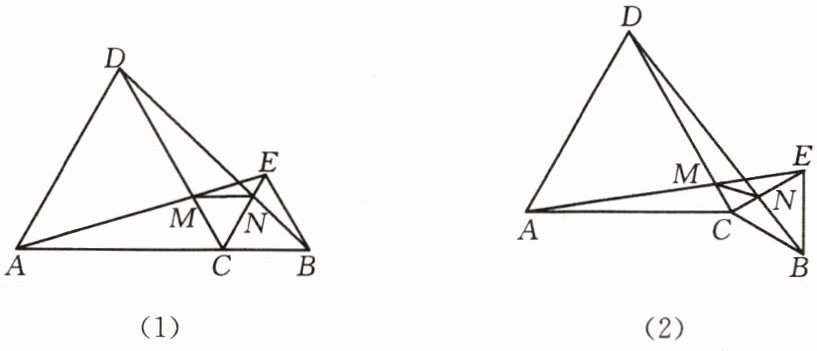
问题 (1)如图(1),已知C是线段AB上一点,分别以AC,BC为边在AB的同侧作等边△ADC和△CBE,AE与DB相等吗?为什么?
(2)当等边△CBE绕点C旋转至如图(2)的位置后,上述结论是否仍成立?为什么?
(3)在上述两图中,设CD交AE于M,CE交BD于N,则△CMN是等边三角形吗?为什么?
名师指导
第(1)(2)小题,由已知条件容易证明△ACE≌△DCB,所以AE= DB。
第(3)小题,在图(1)中可进一步证得△ACM≌△DCN,从而得到CM= CN,又有∠MCN= 60°,所以△CMN是等边三角形。在图(2)中的△CMN中,∠MCN肯定不等于60°,所以△CMN不可能是等边三角形。
解题示范(学生在教师指导下,独立完成)
解:
(2)当等边△CBE绕点C旋转至如图(2)的位置后,上述结论是否仍成立?为什么?
(3)在上述两图中,设CD交AE于M,CE交BD于N,则△CMN是等边三角形吗?为什么?

名师指导
第(1)(2)小题,由已知条件容易证明△ACE≌△DCB,所以AE= DB。
第(3)小题,在图(1)中可进一步证得△ACM≌△DCN,从而得到CM= CN,又有∠MCN= 60°,所以△CMN是等边三角形。在图(2)中的△CMN中,∠MCN肯定不等于60°,所以△CMN不可能是等边三角形。
解题示范(学生在教师指导下,独立完成)
解:
答案:(1)AE=DB。
证明:∵△ADC和△CBE是等边三角形,
∴AC=DC,CE=CB,∠ACD=∠BCE=60°。
∴∠ACE=∠ACD+∠DCE=60°+∠DCE,∠DCB=∠BCE+∠DCE=60°+∠DCE,
∴∠ACE=∠DCB。
在△ACE和△DCB中,
$\left\{\begin{array}{l}AC=DC\\ \angle ACE=\angle DCB\\ CE=CB\end{array}\right.$,
∴△ACE≌△DCB(SAS),
∴AE=DB。
(2)结论仍成立。
证明:∵△ADC和△CBE是等边三角形,
∴AC=DC,CE=CB,∠ACD=∠BCE=60°,
∴∠ACD+∠DCE=∠BCE+∠DCE,即∠ACE=∠DCB。
在△ACE和△DCB中,
$\left\{\begin{array}{l}AC=DC\\ \angle ACE=\angle DCB\\ CE=CB\end{array}\right.$,
∴△ACE≌△DCB(SAS),
∴AE=DB。
(3)图(1)中△CMN是等边三角形,图(2)中不是。
图(1):由(1)△ACE≌△DCB得∠CAM=∠CDN。
∵∠ACD=∠BCE=60°,C在AB上,
∴∠MCN=180°-∠ACD-∠BCE=60°。
在△ACM和△DCN中,
$\left\{\begin{array}{l}\angle CAM=\angle CDN\\ AC=DC\\ \angle ACM=\angle DCN=60°\end{array}\right.$,
∴△ACM≌△DCN(ASA),
∴CM=CN。
∵∠MCN=60°,
∴△CMN是等边三角形。
图(2):∠MCN≠60°,故△CMN不是等边三角形。
证明:∵△ADC和△CBE是等边三角形,
∴AC=DC,CE=CB,∠ACD=∠BCE=60°。
∴∠ACE=∠ACD+∠DCE=60°+∠DCE,∠DCB=∠BCE+∠DCE=60°+∠DCE,
∴∠ACE=∠DCB。
在△ACE和△DCB中,
$\left\{\begin{array}{l}AC=DC\\ \angle ACE=\angle DCB\\ CE=CB\end{array}\right.$,
∴△ACE≌△DCB(SAS),
∴AE=DB。
(2)结论仍成立。
证明:∵△ADC和△CBE是等边三角形,
∴AC=DC,CE=CB,∠ACD=∠BCE=60°,
∴∠ACD+∠DCE=∠BCE+∠DCE,即∠ACE=∠DCB。
在△ACE和△DCB中,
$\left\{\begin{array}{l}AC=DC\\ \angle ACE=\angle DCB\\ CE=CB\end{array}\right.$,
∴△ACE≌△DCB(SAS),
∴AE=DB。
(3)图(1)中△CMN是等边三角形,图(2)中不是。
图(1):由(1)△ACE≌△DCB得∠CAM=∠CDN。
∵∠ACD=∠BCE=60°,C在AB上,
∴∠MCN=180°-∠ACD-∠BCE=60°。
在△ACM和△DCN中,
$\left\{\begin{array}{l}\angle CAM=\angle CDN\\ AC=DC\\ \angle ACM=\angle DCN=60°\end{array}\right.$,
∴△ACM≌△DCN(ASA),
∴CM=CN。
∵∠MCN=60°,
∴△CMN是等边三角形。
图(2):∠MCN≠60°,故△CMN不是等边三角形。